便携式红外寻的防空导弹初制导探索
跃 青
(上海航天技术研究院,上海 201109)
0 引言
寻的制导防空导弹在发射时和进入末制导飞行段前,常需增设初、中制导段或采取探测方法,以实现不同目的。如:对配置作用距离较小导引头的导弹,通过初、中制导将导弹送至距目标较近处,待导引头捕获目标后,再转入精度更高的末制导飞行段,以弥补导引头作用距离较小的不足;发射时加合适的提前角,使导弹在进入有效控制时,具有制导方法所需的前置量,减小进入制导飞行段时的初始偏差,使导弹飞向目标的弹道平直,需用过载降低;改进导弹在发射架(筒)上的支承设计,以减小和补偿导弹发射时的下沉,减小射入偏差,避免导弹因下沉而触地。便携式红外寻的防空导弹一般采用筒式发射,由于作战空域较小,导引头在导弹发射前就已捕获并跟踪目标,故导引头作用距离不够的问题并不突出,但应考虑制导方法所需的前置量和补偿导弹发射段下沉。
传统方法是在导引头捕获目标并开锁后、导弹发射前,射手在高低、方位方向抬高弹轴和给导弹加前置量。该方法存在弊病,如:多了加前置量的操作程序,往往会增加对空作战的复杂度,延误发射时间;前置量由射手根据临战时目标的飞行参数、射击方式等多种因素估计确定,难以准确掌握,且易产生误差和失误;不便于本类导弹的扩展使用,如多联装车载、弹炮结合、装舰作为舰-空导弹和装机作为空-空导弹等。
为省去导弹发射时加前置量和抬高弹轴等程序,能对目标进行直瞄发射,可采用以下两项技术:导弹发射出筒后加侧向力控制改变弹的姿态角以提供弹道所需的前置角;导弹在发射时锁偏导引头光轴,使光轴和与光轴平行的瞄准线在弹轴下方,射向高于视线,以补偿导弹发射时的下沉。本文称这两项技术为初制导(严格来讲,发射时抬高射角不属于制导范畴)。本文对便携式红外寻的防空导弹的初制导进行了探索和讨论。
1 前置角提供
1.1 期望前置角取值
采用比例导引法时,导弹飞行中速度矢量在空间的转动角速度与弹目连线即视线的角速度成正比,有
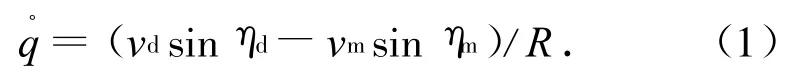
式中:R为弹目的相对距离;vd,vm分别为导弹和目标的飞行速度;ηd为导弹速度矢量与视线的夹角(即前置角);ηm为目标速度矢量与视线的夹角。当导弹进入比例导引的弹道时,视线角速度趋于零,有

对应的期望前置角
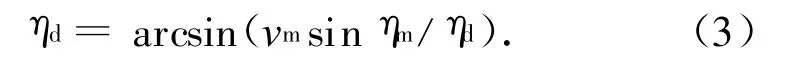
初制导的侧向力控制系统在导弹发射离筒速度较小时改变弹的姿态角,可在选定的设计条件下获得所期望的前置角。
由式(3)可知:前置角与目标的飞行速度、目标速度矢量与视线的夹角,以及导弹的飞行速度有关。由于导弹发射时目标视线的角速度

可近似地认为vmsinηm在发射后短时间内变化不大,代入式(3)可得
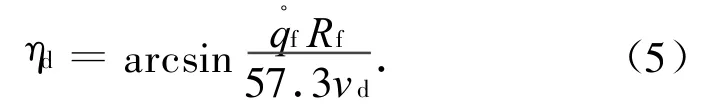
式中:Rf为导弹发射时弹目的相对距离;为导弹发射时的目标视线角速度。导引头在捕获目标后可测量并提供目标视线角速度,故需确定的是Rf,vd。
由于在发射初期,导弹处于主发动机一级工作的亚、跨声速飞行段,气动参数变化剧烈,操纵效率很低,而当速度大于声速,进入巡航飞行后,气动参数变化趋于平稳,导弹具较大的可用过载和较好的机动能力,可适应弹速变化,将导弹引入比例导引的轨道并符合精度要求。为能在近界命中目标,取近界作为设计条件较合适。此设计状态下,可取导弹的vd为巡航速度,导弹发射时弹目间的相对距离可能出现的最大值
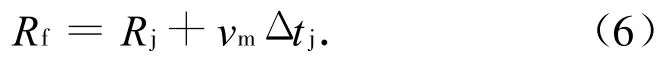
式中:Rj为杀伤区近界距离;Δtj为导弹飞至近界所需时间。用式(6)估算导弹发射时弹目间的相对距离时,vm宜选择经常出现的、适应性较强的值。
将导弹的巡航速度vd,Rf代入式(5),即可估算出期望前置角值。
若能满足射击近界目标时的前置角要求,则在射击较远目标时,由于导弹飞行距较远,受控时间较长,能消除各种初始偏差将弹导入比例导引轨道,即同样可满足杀伤区其他点的要求。
期望前置角虽是选择侧向力控制系统能量的依据,但受条件限制,对它的推算并不严格,且在导弹发射后发动机一级工作的加速段,期望前置角随激烈变化的弹速相应变化,即目标值的确定、侧向力的产生和控制均十分粗糙与近似。但增加侧向力控制,对简化发射导弹时的操作和改善导弹飞行状况的效果明显。
1.2 侧向力控制方案
对旋转弹体单通道控制的导弹,弹上控制系统采用电动舵机时的侧向力系统控制方案结构如图1所示。其中:电动舵机通过伞形齿轮付减速并驱动前舵轴,舵轴带动与其联动的分配阀将来自燃烧室的燃气按舵偏规律分配至与舵平面垂直且相背的2个喷管,依靠排出燃气的反作用力产生侧向推力。此推力与前舵偏转形成的操纵力方向一致,且与舵偏角成比例。推力合成的力矩使弹体产生绕重心转动的角加速度和角速度,改变弹的姿态,构成所需的前置角。

图1 侧向力系统控制方案结构Fig.1 Structureof cateral force control scheme
在不影响导弹正常发射的前提下,侧向力控制系统的工作宜早、短。可选择发射发动机工作结束后、导弹即将离筒时开始工作,并尽量减少与主发动机工作的重叠时间。因为在此时段,弹速较低,气动恢复力矩较小,改变弹姿态较易,且可使在主发动机点火后导弹的加速度和速度更接近期望的前置角方向,易获得更好的效果。但工作时间又不能太短,因为当导弹转动惯量已定时,期望前置角与推力合成总冲量矩有关,工作时间越短,一方面侧向推力合成的力和力矩就越大,会对弹体结构造成冲击,另一方面对单通道控制的旋转导弹来说,在此时段内包含的弹体旋转次数就越少,会使侧向推力合成的力和力矩误差增大(此状况在控制系统采用电动舵机迫使导弹发射出筒转速降低时会更严重)。综合来说,一般认为在侧向力控制系统工作时段内,弹体旋转次数控制在6~12转较宜。
设最大的侧向推力为Fmax,对应最大的舵偏角为δmax,旋转导弹控制系统电动舵机采用正弦控制,舵偏角为δ时的侧向推力
合成侧向推力

侧向推力对弹体重心的合成力矩
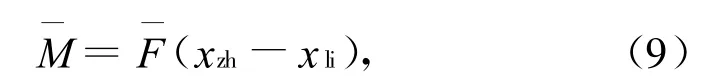
导弹采用继电式燃气舵机控制,侧向力系统产生的最大合成侧向推力
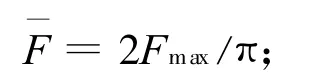
对弹体重心最大合成侧向推力的力矩
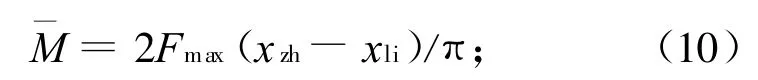
在合成侧向推力矩的作用下,导弹形成的角加速度

若认为合成推力为常值,则导弹形成的角速度
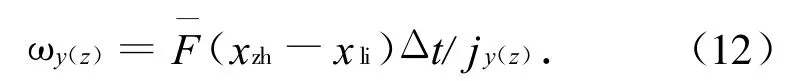
式中:δ为前舵偏角;xzh为弹体质心位置;xli为侧向推力作用点位置;jy(z)为弹体对过质心的y、z轴的转动惯量。
由式(11)可知,当在弹体参数确定时,侧向力控制系统的推力总冲量F0Δt与产生的角速度成比例。
侧向力控制系统的推力消失后,角速度会因惯性而继续维持,直至在大气阻尼和恢复力矩作用下减小、消失,此时的转角应为期望前置角。
2 发射下沉补偿
2.1 发射时的弹筒分离运动
发射中发动机点火工作后,导弹先是沿发射筒内表面向前滑动同时绕自身纵轴转动,当前支承环离筒后,由于弹的重心位于后支承前,形成一低头力矩,故在上述运动的基础上又增加了俯仰方向的低头转动。分离运动状况和参数取决于弹筒结构与配合尺寸。
对分离运动的分析和计算表明:弹筒分离时导弹存在的附加俯仰角Δϑ及其角速度与发射角θ0的余弦成比例。因附加俯仰角对其后的飞行弹道影响很小,故可不予考虑,而俯仰角速度在导弹速度和恢复力矩较小且无动力的条件下,可使导弹继续低头,改变弹的俯仰姿态和飞行方向,是初始弹道下沉的主要原因,需予以补偿。
2.2 补偿措施
减小下沉,消除由此引起的影响,常用方法有:
a)增大导弹发射时的加速度,减少发射时导弹在发射架上(筒内)的停留时间,缩短前支承环离筒后低头力矩的作用时间,以减小分离时导弹的;
b)改进设计,合理选择支承位置和结构形式,以减小导弹在发射过程中的低头力矩,甚至使前、后支承同时脱离弹体,使导弹在发射过程中的低头力矩为零;
c)发射时抬高弹体轴线,以补偿下沉并消除下沉的影响。
当导弹和武器系统方案已初步确定,各种参教和结构基本明确时,发射时可抬高弹体轴线。理论上,弹体上抬角度只要等于导弹出筒时由引起的弹体俯仰姿态角的变化(即下沉角)即可。但实际问题并不简单,因为下沉角不是常量,随发射角的增大而减小,当采用直瞄发射时,弹体上抬的角度涉及导引头电锁锁偏角和光学瞄准具光轴的安装角,难以根据发射角的大小随时调整,只能为常值,这就使弹体上抬角难以确定。若为保证导弹在小发射角状态发射时不发生触地,所需弹体上抬角度则较大,故在大发射角状态射击目标时易发生因上抬角过大而使飞行弹道不理想的情况;若所取弹体上抬角度偏小,则在射击低空目标时又可能因下沉过大而使导弹堕地。
3 俄制针式防空导弹初制导系统
该导弹的初制导系统设计结合了旋转导弹单通道控制的特点,利用导引头可能提供的有限数据,通过加侧向力和上抬弹体较好地解决了发射时需加前置量的问题,导弹具有直瞄发射功能。研究和分析发现:导弹采用继电式燃气舵机控制;发射时弹体纵轴相对瞄准具光轴(即视线)上抬10°;侧向力系统控制电路的工作时间为0~1 s;侧向力的作用时间为0.1~0.7 s;侧向力为8 N;侧向力的方向与前舵偏转后产生气动控制力的方向相同,其数值可表示为

式中:K为合力系数。
弹体重心形成的力矩
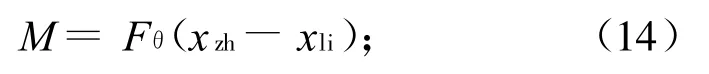
侧向力系统产生的合成侧向推力

弹体重心合成侧向推力的力矩
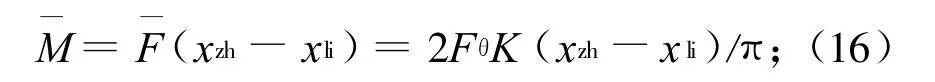
控制律
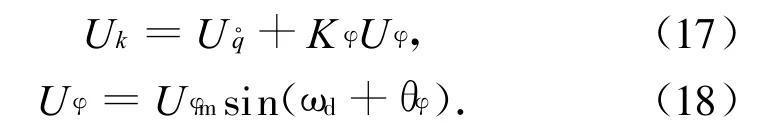
式中:ωd为弹体绕纵轴的转速;θφ为目标相位角;Uk为控制信号;为主控信号;Kφ,Uφm为系数。
由控制律可知,侧向力系统的控制信号包括两部分:
b)初制导增加的控制信号KφUφ主要与弹轴、视线间的夹角φ有关,用于防止由增加的初制导引发的非理想状况发生,但在导弹发射1 s后就不起作用。
以下讨论与初制导有关的增加部分。
Uφm取值为:φ>15°时,Uφm=7.25;φ≤15°时,Uφm=28sinφ。Kφ取值为:当φ增大时,若φ>15°则Kφ=-0.4,若φ≤15°则Kφ=0.26;当φ减小时,若φ>15°则Kφ=-0.4,若φ≤15°则Kφ=0。由此,可得不同φ时的Uφm,Kφ及KφUφm如图2所示。
由图2可知:当φ较小(≤15°)时,若φ增大,则KφUφm为正值且随φ增大而变大,若φ减小,则KφUφm为零;当φ较大(>15°)时,不论φ增大还是减小,KφUφm均为负且保持常值。
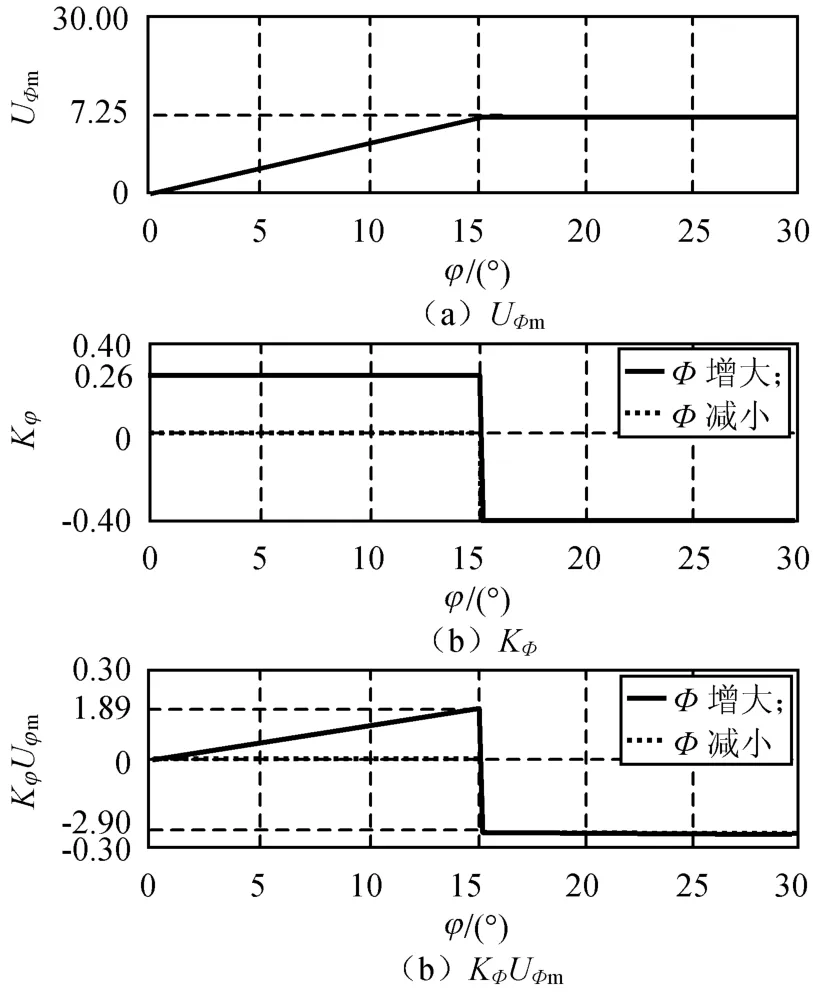
图2 不同φ时的Uφm,Kφ,KφUφmFig.2 Uφm,Kφ,KφUφmunder dif ferentφ
因φ定义为弹轴与目标视线的夹角。导弹发射后,在侧向力系统工作的0~1 s(真正起作用的是0.1~0.7 s)短暂时间段内的φ,其实质是在弹体上抬角度确定条件下,对弹体姿态角和视线角的大小和变化趋势的影响。影响弹体姿态角和视线角大小和变化的主要因素有作战方式、目标视线角速度、发射参数和在侧向力控制系统作用下弹体姿态的改变等。其中:作战方式可分为迎攻、尾追或侧攻,决定了视线角速度的方向;目标视线角速度的大小、方向和变化取决于目标的飞行速度、高度、航向和距离等参数,事先无法预测,在导引头捕获目标后可由导引头实时测量并给出;发射参数主要指射角的大小,影响导弹发射出筒时的下沉量,使弹体倾角减小,其方向和变化规律较固定;侧向力控制系统作用下弹体姿态的改变与设定的控制律及合成侧向推力矩大小等因素有关,主要受制于目标视线角速度与制导回路中合力系数随视线角速度的变化关系,另还与φ相关。
由于存在惯性,导弹发射出筒时的下沉和侧向力控制引起的弹体姿态变化在导弹离筒后和侧向力消失后仍会延续。因此,影响最终前置角的因素较多且关系复杂,需根据导弹的实际情况,经细致分析、计算甚至试验,才能获得确切的结果。
对俄制针式便携红外寻的防空导弹的初制导系统实例进行分析,可认为:
a)弹轴相对视线上抬10°可弥补导弹发射出筒时的下沉。因为在射击远界低空低速目标时,迎攻和尾追的视线角速度均很小。另外,由于射角较小,导弹发射出筒时的下沉较大,故在下沉的作用下,φ呈现减小趋势,而控制律中,由于视线角速度很小,除形成期望前置角的较小以外,KφUφ值由于φ减小,也始终不会大于零,两种因素造成侧向力控制系统使弹体姿态改变的合成侧向力矩较小,即无使弹抬头防止其堕地的措施。
b)控制律具有在大射角迎攻射击中等视线角速度目标时,在侧向力控制系统作用下,防止发生前置角过大的功能。因为,此时虽然下沉和视线角速度均会使φ减小,但量值较小,而合力系数较大,导致侧向合力矩也相应增大,可能形成过大的前置角。
c)在侧向力控制系统工作的时间段内,不希望出现过大的φ,因为一旦φ大于15°,KφUφ值立即突跳至负值,阻止φ继续增大。
分析认对针式导弹初制导系统的研究还存在以下问题:
a)导弹在发射过程中影响φ和前置角的参数的变化应是连续和有规律的,可是针式导弹的控制律中KφUφ值在φ在15°前后出现突跳。若能通过某简单函数或其他方式更形象、确切地描述KφUφ值随φ的变化关系,则可使其适应性更强。
b)初制导系统虽然可明显改善飞行弹道,减小杀伤区近界距离,仅是一种近似的开环修正补偿,不可能也没必要变得非常精细和复杂,但其变化趋势和量值应尽可能符合实际需要。
c)应寻求更完善的初制导方案。目前已有的初制导方案虽能一定程度解决导弹发射时加前置量和下沉的问题,但由于需抬高弹轴,在实施和使用过程中还存在不便。若能在控制律中增加发射时能使弹的姿态角上抬的部分,则效果更为理想。
4 结束语
本文对便携式红外寻的防空导弹初制导及其必要性、实现技术途径、需考虑的因素和参数选定方法等进行了定性研究,并对俄制针式便携红外寻的防空导弹的初制导系统进行了分析。在设计导弹初制导系统时,还需根据各导弹的特点、结构和参数而具体灵活应用。因为导弹在发射筒内支承形式、位置和质量、质心的不同,发射发动机推力特性的差异,都会影响导弹发射时低头力矩大小和作用时间,进而影响导弹发射时的下沉量;导弹的速度特性、对付目标的速度、杀伤区近界等参数影响期望前置角,产生侧向力喷管可安置的位置关系相同的力能产生的力矩大小,这些因素均会影响侧向力系统设计参数的取值;若弹上采用电动舵机正弦控制方式,则还需考虑舵面偏转速度降低迫使弹体转速变缓对侧向力控制系统的工作时间调整,以及形成控制合力效率降低对侧向力控制系统需用能量增大等的影响。

