高速旋转圆筒内流场的数值研究
周陈龙,丁保庚,王 颖,李兴华
(核工业理化工程研究院,天津 300180)
长期以来,国内外在研究高速旋转流场时,一直以等温刚体旋转状态为基础,对纳维-斯托克斯方程(N-S方程)进行线形化求解。大量的研究已证明,旋转圆柱筒内流场不会发生不稳定情况[1],但现在考虑的是高速短圆柱筒转速很大,其内部流场的最高马赫数达到了7左右,这时流场平衡时的状态,是一个非常重要而在一些工程中又急需解决的问题。
关于高速旋转流场的试验研究一直是我们的一个薄弱环节。由于圆柱筒高速旋转,其内部流场径向跨越了分子流、过渡流、粘性流区域,目前还未找到一种合适的、不干扰流场的、具有高精度的测量高速强旋转流场的方法。因此,采用数值解法进行模拟显得十分必要。
本工作利用数值分析法,采用二阶迎风格式、总能守恒模型,对封闭状态下高速旋转的短圆柱筒内的三维流场进行数值研究,并与理论计算结果进行对比分析。
1 等温刚体旋转状态下的平衡解[2]
在等温刚体旋转状态下,圆柱筒内气体角速度与圆柱筒角速度相等,温度是均匀的,都等于初始状态温度T0,故有:

式中:vr为气体速度径向分量;vθ为气体速度角向分量;Ω为圆柱筒角速度;r为半径;vz为气体速度轴向分量;T为气体温度。
如果用p和ρ来表示这种状态下的压强和密度,给定的边界条件是圆柱筒侧壁处的压强pw和密度ρw,则p和ρ的表达式为:

将相关参数代入式(1)和(3)中,得到等温刚体旋转状态下的速度和压强分布(图1、2)。

图1 等温刚体速度分布Fig.1 Velocity distribution in isothermal rigid body rotational state

图2 等温刚体径向压强和-ln(p/pw)沿径向分布Fig.2 Radial pressure distribution and-ln(p/pw)radial distribution in isothermal rigid body rotational state
2 物理模型
目前研究的短圆柱筒是高速旋转设备,内部绝大多数气体均集中在靠近边壁的区域。径向上,流场跨越了分子流、过渡流、粘性流等流动区域。采用封闭模型,选取高度z与半径r比为1∶2的短圆柱筒,得到的计算模型如图3所示。

图3 计算模型Fig.3 Computing model
3 数学模型
3.1 基本假设
基本假设如下:1)圆柱筒内的流体假设全部为连续介质,流体运动遵循纳维-斯托克斯方程;2)流体所受的重力与离心力相比可忽略;3)忽略由于辐射或其他原因传到流体上的热量;4)流体的粘性系数、热传导系数和等压比热均为常数;5)对于可压缩流体的膨胀粘性系数采用斯托克斯假设,令膨胀粘性系数等于零;6)流体的状态方程由完全气体定律来描述。
3.2 控制方程
根据前面所作的基本假设,圆柱坐标系下流体的运动基本方程如下。
连续方程:
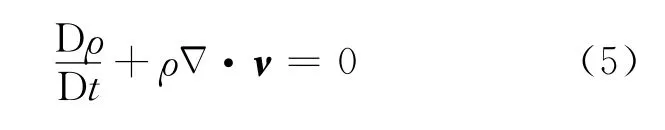
动量方程:

能量方程:
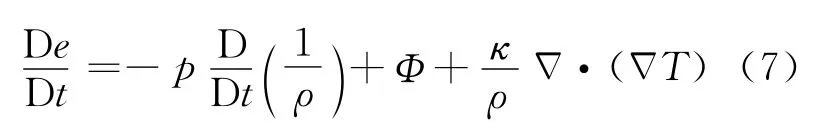
状态方程:

其中:
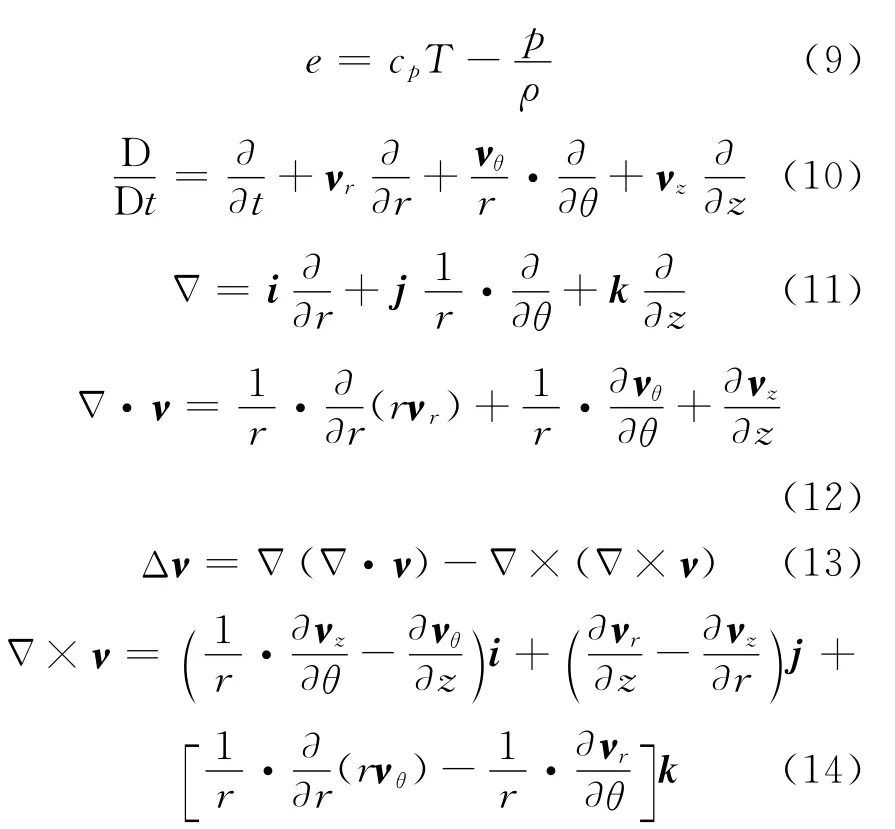
式中:e为内能;κ为热传导系数;μ为粘性系数;Φ 为粘性耗散函数;cp为等压比热容;i、j、k分别表示r、θ、z方向的单位矢量。
3.3 初始条件和边界条件
计算采用圆柱坐标系。初始条件采用等温刚体旋转条件:vr= 0m/s;vθ= Ωr;vz=0m/s;p(r)= pwexp{- A2[1 - (r/ra)2]};T=300K。
边界条件:上、下边界和侧壁以vθ旋转,T=300K,使用壁面无滑移条件。
4 计算方法
4.1 计算网格
网格生成的质量直接影响流场数值求解的精度和稳定性,所生成的网格须满足贴体性、光滑性、合理分布性及正交性的要求。
利用ICEM CFD软件通过创建独立于几何模型的块体结构近似几何模型,将块拓扑中的网格自动映射到几何模型上的方法,得到六面体单元。为了改善近壁局部的边界层网格精度,采用了O-grid网格方法。由于短圆柱筒内径向压强成指数分布,在靠近边壁处进行了高度加密处理,最后得到约11 708个单元(图4、5)。

图4 计算模型整体网格Fig.4 Whole mesh of computing model

图5 网格剖面图Fig.5 Section plan of mesh
4.2 计算方法简介
本工作采用ANSYS CFX软件进行计算求解,该软件采用基于有限元的有限体积法。采用由瞬态计算得到稳态解的方法,计算坐标系为柱坐标系,按总能守衡进行求解,计算采用的模型为剪切应力输运(SST)k-ω模型。
SSTk-ω模型是二方程模型中的一种。与标准二方程k-ω 模型相比,SST k-ω 模型中增加了横向耗散导数项,在湍流粘度定义中考虑了湍流剪切应力输运过程。因此,该模型提高了强逆压梯度或强顺压梯度的非平衡湍流边界层及分离流计算能力[3],适用于本工作的计算。
5 计算结果及分析
工作介质的相关参数采用参考压强为0.1MPa、温度为300K时的值。计算采用4种方案:大时间步长(情况1)、小时间步长(情况2)、计算域旋转和小时间步长(情况3)、高密度网格下的小时间步长(情况4)。所有计算方案均在3.3节的计算条件下进行。
5.1 大时间步长计算
计算采用瞬态计算的方法,初始步长为1×10-7s,推进几百步后,时间步长改为1×10-4s,收敛效果很好。图6示出纵切面压强等值线、轴向中心横截面径向压强、纵切面速度、轴向中心横截面处径向速度分布。从图6a可看出,压强呈轴对称分布,从中心区域沿径向逐渐增大,在外边壁处达到最大。压强分布近似与轴向坐标z无关,只是径向坐标r的函数。从图6b可看出,在0.5z的中心横切面上,压强在径向上的分布与刚体旋转情况下的分布存在很大差异,在中心处压强约为760Pa,远大于刚体假设时的值,且并未体现出指数增长的规律,径向压强梯度较小,压强在边壁处约为3 260Pa,与刚体旋转时的15kPa的边壁压强相差很大。
从图6c可看出,速度呈轴对称分布,中心处速度最小(为0m/s),沿径向逐渐增大。在圆柱筒中部速度分布与轴向坐标基本无关,只是径向坐标的函数,但在靠近上、下边界处,速度明显增大。从图6d可看出,速度在中心区域基本呈线性分布,当r>0.8ra时,速度急剧增大,在靠近边壁的区域内表现出很大的速度梯度。速度沿径向的分布与刚体旋转的速度分布(图1)存在很大差异。
上述结果确实是方程的解,总计算时间相当于圆柱筒旋转约3 200圈,解很稳定。但试验数据证明这是一非物理解。研究寻找其物理解的方法将是很重要的任务,具有重要学术意义和实用意义。
5.2 小时间步长的计算
计算条件与5.1节完全相同,但采用小步长1×10-8s,观察用小步长能否得到物理解。
轴向中心横截面处圆周速度沿径向分布和径向压强分布示于图7。由图7a可看出,速度仍大幅偏离刚体速度分布。由图7b可看出,中心区域压强大幅提高,这与圆周速度大幅低于刚体旋转速度的现象吻合。由于仅计算10 000步,累计时间1×10-4s,未达到稳态,这可由图7a的曲线形状反映出,但其趋势已非常清楚,可以说,在这种情况下,采用小步长的方法仍不可能得到物理解。
5.3 计算域旋转和小时间步长的计算
采用3.3节的计算条件,计算域以vθ旋转,计算坐标系为柱坐标系,按总能守衡进行求解,使用各向异性能考虑哥氏效应的雷诺应力湍流模型。采用小步长1×10-8s计算。
圆周速度、轴向速度、径向速度等值线示于图8。轴向中心横截面处圆周速度沿径向分布示于图9a。由图8、9a可看出,圆周速度基本上是刚体转速。由图8b、c可知,存在有轴向速度和径向速度,但数值很小,每秒仅几米,说明可近似认为是刚体旋转速度。
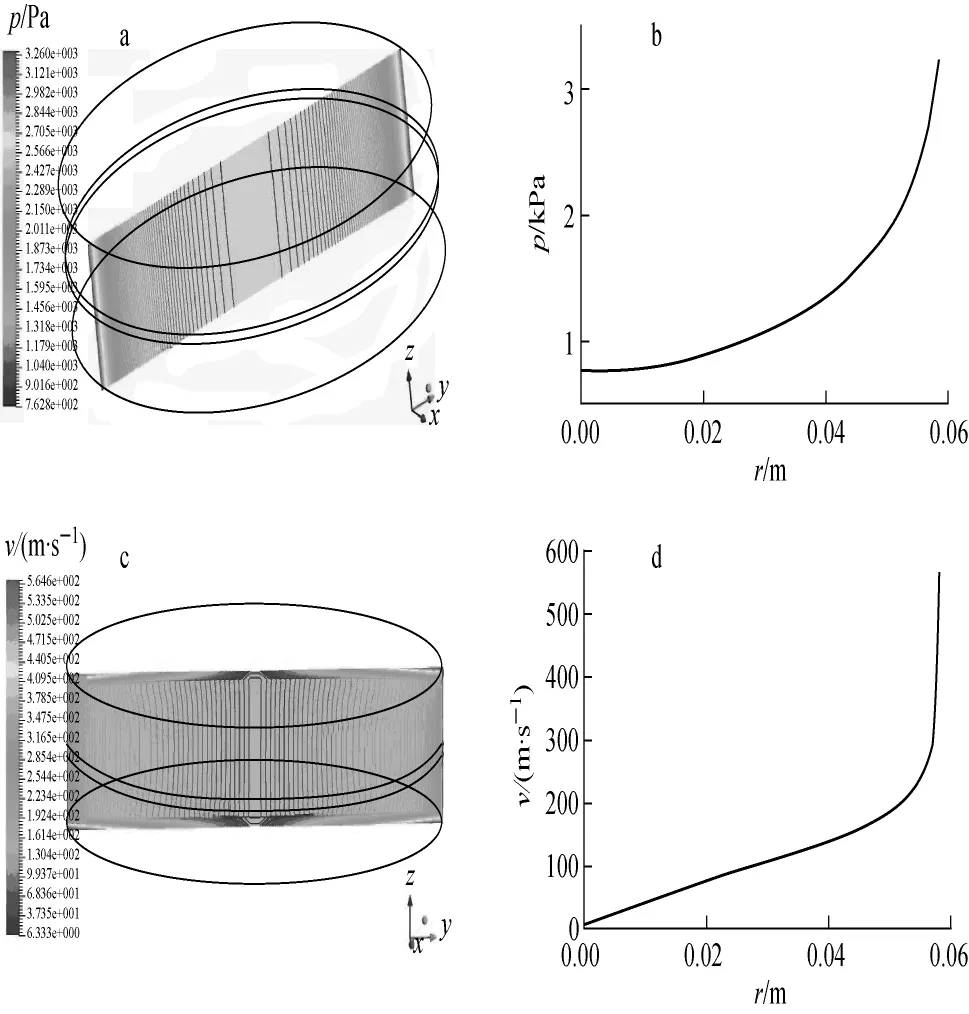
图6 情况1的纵切面压强等值线(a)、轴向中心横截面径向压强(b)、纵切面速度(c)、轴向中心横截面处径向速度(d)分布Fig.6 Isobars at longitudinal section(a),radial pressure distribution at center transverse section(b),velocity distribution at longitudinal section(c)and radial velocity distribution at center transverse section(d)in case 1

图7 情况2下轴向中心横截面处圆周速度沿径向(a)和径向压强(b)分布Fig.7 Circle velocity radial distribution(a)and radial pressure distribution(b)at center transverse section in case 2
轴向中心横截面处径向压强分布和温度等值线分别示于图9b、10。由图9b、10可见,中心区域为300K,侧壁附近达324K,不是等温流动,而且,压强沿径向的变化与等温刚体压强分布(图2a)也有很大差别。
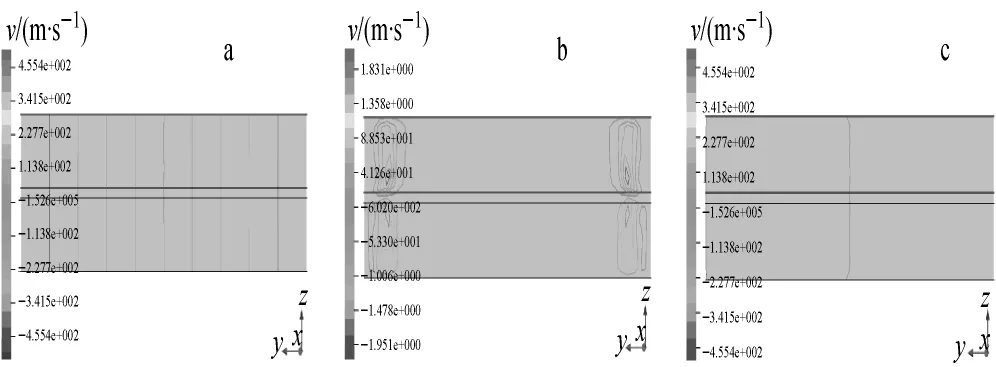
图8 情况3下的圆周速度(a)、轴向速度(b)、径向速度(c)等值线Fig.8 Isoline of circle velocity(a),axial velocity(b)and radial velocity(c)in case 3

图9 情况3下轴向中心横截面处圆周速度沿径向(a)和径向压强(b)分布Fig.9 Circle velocity radial distribution(a)and radial pressure distribution(b)at center transverse section in case 3
5.4 高密度网格下小时间步长的计算
对图4的网格在圆周方向和径向进行加密,总的网格数约为241 600,比原来扩大约22倍。用1×10-7s的时间步长计算,稳态结果如图11~13所示。

图10 情况3下温度等值线Fig.10 Isotherms of temperature in case 3
从图11a可见,计算结果接近5.3节的情况。圆周速度基本是线性分布,存在轴向速度和径向速度,但数值很小,可近似认为是刚体旋转速度。从图11b可看出,压强呈指数分布状态,与理论计算结果相比,趋势上基本相同。从数据上比较,在中心部位,数值计算得到的压强是几Pa,而非等温刚体得到的10-6~10-7Pa,即从实验结果分析得出的中心区域压强和数值计算得到的中心区域压强基本吻合。由图12、13可见,中心区域的温度基本保持在300K左右,而边壁附近的温度在322K左右,不是等温流动。
因此,采用高密度网格的小步长计算能得到物理解,与理论计算结果相比,数值计算结果更符合实际情况。
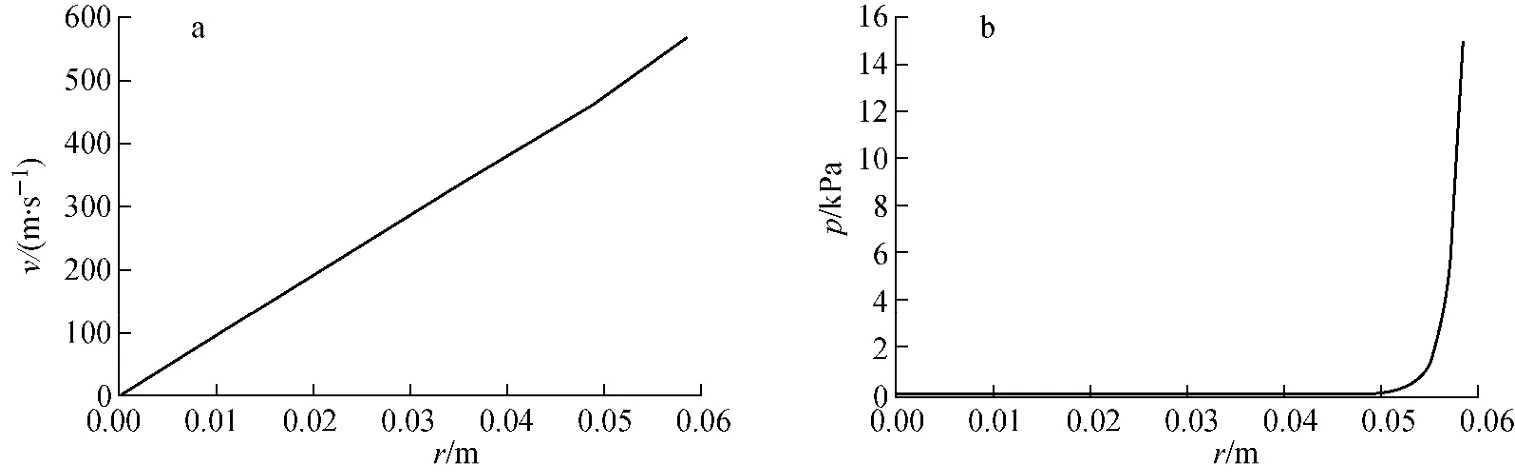
图11 情况4下轴向中心横截面处圆周速度沿径向(a)和径向压强(b)分布Fig.11 Circle velocity radial distribution(a)and radial pressure distribution(b)at center transverse section in case 4
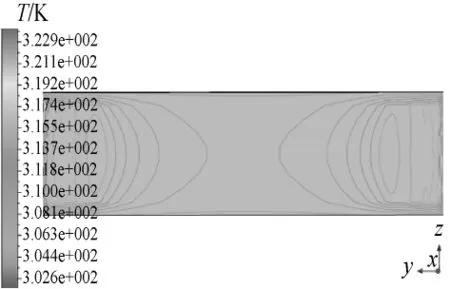
图12 情况4下的温度等值线Fig.12 Isotherms of temperature in case 4
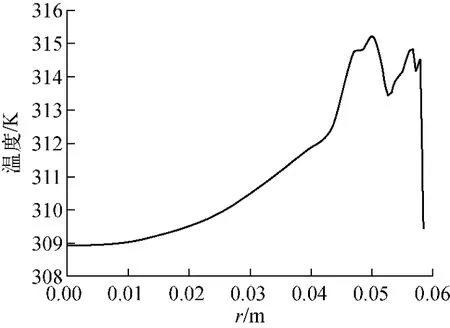
图13 情况4下轴向中心横截面处径向温度分布Fig.13 Radial temperature distribution at center transverse section in case 4
6 结论
对本工作研究的封闭的短圆柱筒而言,当圆柱筒转速很大时,其内部流场流动的最高马赫数达到了7左右。研究表明,只有在一定的计算条件下,数值计算才能得到物理解。而在能得到物理解的情况下,高速旋转圆柱筒内流场平衡时不是等温状态,但速度和压强分布基本保持刚体旋转状态。
[1]陈懋章.粘性流体动力学基础[M].北京:高等教育出版社,2002.
[2]张存镇.离心分离理论[M].北京:原子能出版社,1987.
[3]朱自强.应用计算流体力学[M].北京:北京航空航天大学出版社,1998.
[4]杜庆华.工程力学手册[M].北京:高等教育出版社,1994.

