电动振动台模型辨识方法及其应用的研究
郭继峰,任万滨,康云志,翟国富
(1.哈尔滨工业大学 军用电器研究所,哈尔滨 150001;2.东北林业大学,哈尔滨 150040)
冲击试验是一种力学环境与可靠性试验,主要目的在于设法产生某种冲击激励以检验被试系统的强度和性能[1]。产生规定冲击波形的方法很多,主要包括跌落冲击试验机、气动式冲击机和电动振动台等。其中电动振动台由于具有激振频率范围宽、推力大、易于自动和手动控制的特点,因此可通过数字控制系统完成各种典型脉冲及其它冲击波形的冲击试验。以往主要应用波形幅值均衡法和传递函数均衡法实现时域波形控制[2~3],控制过程中反复修正时域波形幅值、延迟时间等相关参数,或者不断确定试验系统的传递函数,再利用规定波形的傅里叶变换得到新的驱动波形信号,从而完成闭环修正过程。此类方法涉及傅里叶变换、闭环控制等环节,不仅控制系统对硬件的要求较高,而且所模拟的冲击波形参数(包括幅值、时间延迟等)受噪声和设备等因素影响明显。
电动振动台作为振动与冲击环境试验的主设备,其传递函数模型的辨识与估计是开展振动控制技术研究和振动试验仿真的必要环节。文献[4-6] 采用了基于测量频率特性估计振动台模型参数的方法,但操作繁琐不利于工程应用。本文基于电动振动台的动力学和电学耦合模型,提出了一种以冲击信号作为激励的振动台模型传递函数进行系统辨识的方法。通过仿真结果与试验结果的比较以及传递函数参数的估计,验证了模型辨识方法的准确性与有效性。最后,基于所辨识的振动台传递函数,对振动台模型进行PID仿真控制实现了符合标准的冲击试验波形,且一致性好。
1 电动振动台模型的建立
为简化分析,做两点假设:① 电动振动台只有一个自由度;② 气隙磁通密度为常数。忽略滤波器情况下电动振动台模型的等效框图如图1所示,由电磁部分可得式(1)~式(3),机械部分可得式(4)。
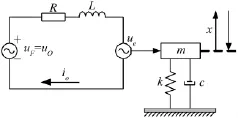
图1 电动振动台等效参数模型Fig.1 Equivalent model of electrodynamic vibration shaker
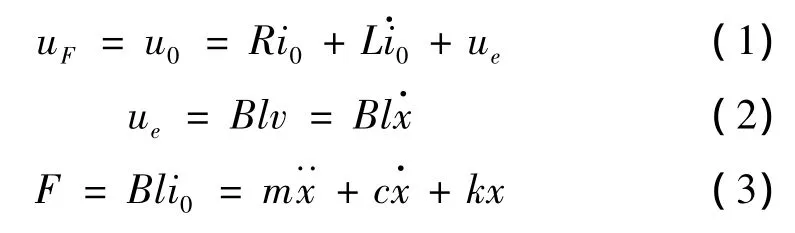
其中uF为输入电压;u0为线圈电压;R为等效电阻;L为等效电感;B为气隙磁通密度;F为电动力;m为电枢和工作台质量;c为阻尼比;k为弹性系数;x为台面位移;l为电枢等效长度;ue为振动台等效电压;i0为驱动电流。
将式(2)、式(3)代入式(1)中,得:
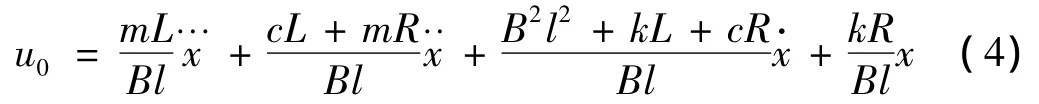
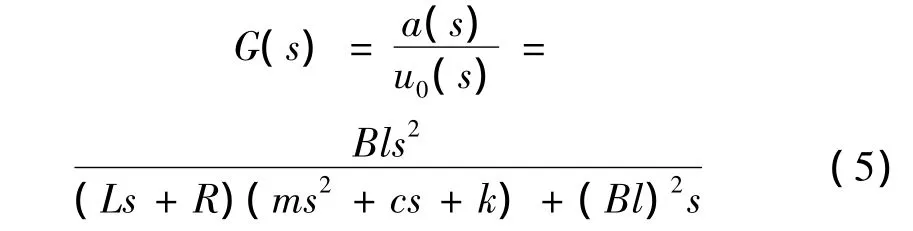
由此可确定电动振动台的模型阶次为3阶。
作用在电枢上的非正弦激励导致无法准确控制电动振动台的加速度。电枢电阻和电枢电感的非线性会使其随激励信号频率改变而改变,振动台台面在加载被测元件后质量的改变也会使模型改变[7]。上述原因使得很难通过测量系统全部参数得到系统模型,也就无法通过理论分析和测量的方法得到可以应用到实际中的模型。
将式(5)转换成零极点表示形式:

系统连续传函为三阶,同时含有三个极点和三个零点。为满足数字控制的要求,将理论模型的连续传递函数转换为离散传递函数,从而完成系统辨识。将零阶保持器串入传递函数中,由Z变换得:
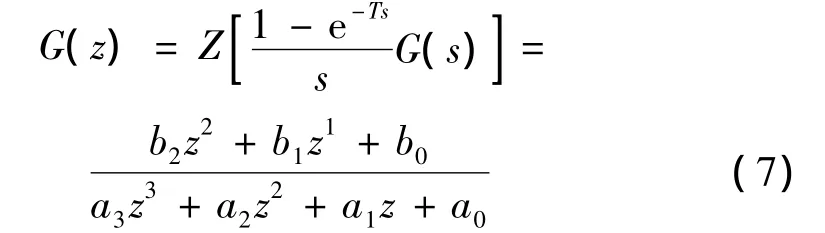
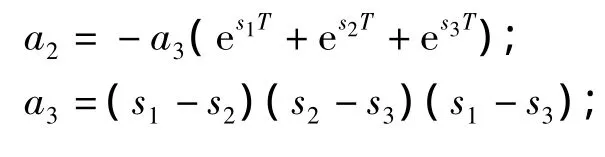
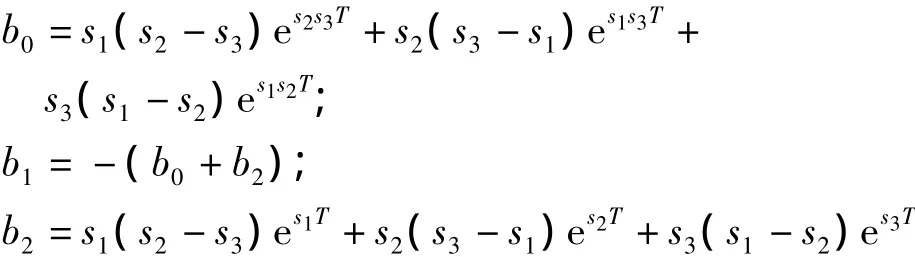
2 电动振动台模型辨识方法
电动振动台模型辨识即指其传递函数的确定过程。传递函数的获取是电动振动台实现精确控制的关键。图2所示为电动振动台系统辨识流程。全部模型辨识过程包括以下步骤:
(1)建立振动台模型,获得连续传递函数G(s),确定模型阶数、零点和极点数;
(2)将连续传递函数G(s)变换得离散传递函数G(z);
(3)采集振动台输入电压和输出加速度信号,经过滤波、去除趋势项环节后,进行系统辨识,达到辨识加速度输出与测试结果相似,以此作为模型参数;
(4)将步骤(3)中所得离散模型变换为连续模型,将其相关参数代入至G(s)模型中,并以步骤(3)中输入输出信号进行参数估计;
(5)若步骤(4)中的参数估计不收敛,则更改迭代规则直至计算收敛,最终获得模型参数。
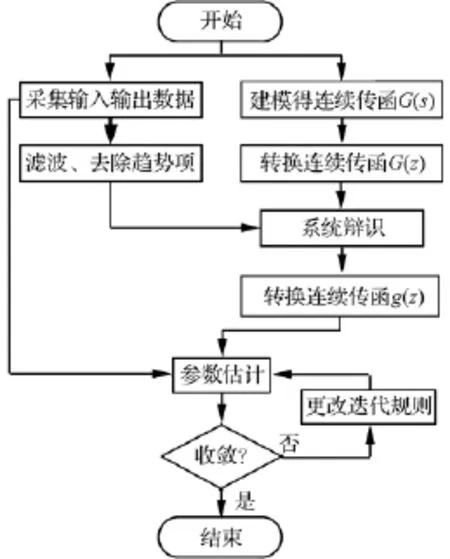
图2 电动振动台辨识流程图Fig.2 Identification flow chart
3 输入信号对模型辨识的影响
系统辨识的结果与振动台输入电压信号具有一定的相关性,激励信号包含系统的信息越多,辨识结果越接近真实模型。本文选择两类信号作为比较参考,即一定范围频谱的随机信号和与实际应用最接近的冲击信号作为输入激励。
3.1 随机信号
以一段频率范围为50 Hz~100 Hz覆盖83.33 Hz的随机信号作为振动台输入电压信号,采用高精度Agilent示波器5 012 A测试振动台输出加速度信号,测量时间为100 ms,采样50 000个数据点,采样周期为2μs。
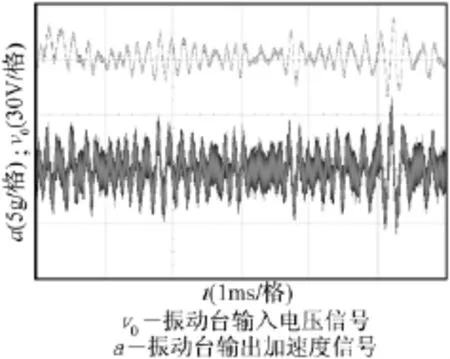
图3 随机信号激励与响应Fig.3 Excitation and response of random signal
将图3所示的振动台输入电压随机信号和输出加速度信号数字低通滤波后,选取ARX模型,采用最小二乘法进行辨识,得到离散传递函数为:
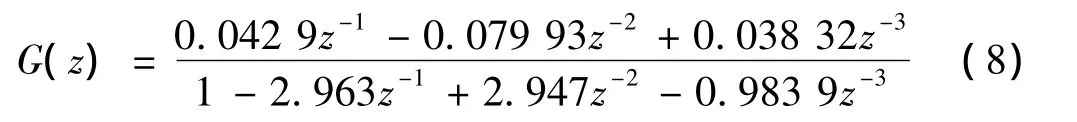
通过系统辨识得到的加速度输出与和试验测试所得输出示于图4中,计算可得两者相似度为75.31%,然而在所得辨识模型上加载冲击信号时,模拟输出与实际输出结果的相似度不足20%。
3.2 冲击信号
图6所示为一段宽度为6 ms的半正弦冲击信号作为振动台输入电压信号和测试所得的振动台输出加速度信号。参照前述的数据处理和辨识参数过程,得其离散传递函数为
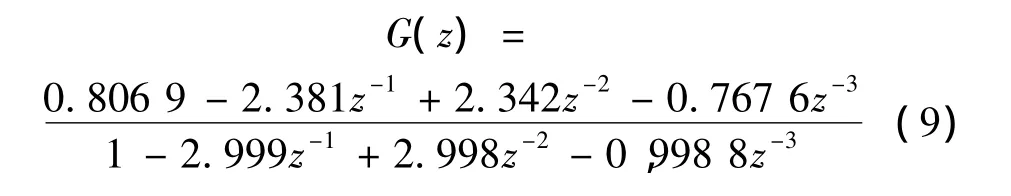
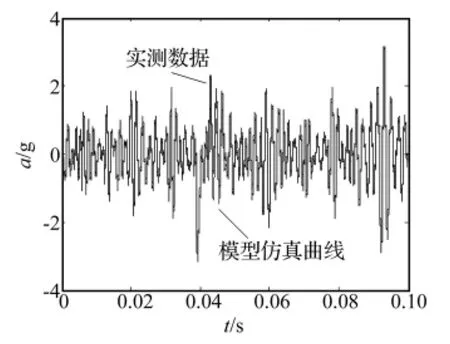
图4 随机仿真输出与实际输出Fig.4 Simulation and test results of random signal

图5 加速度响应结果的比较Fig.5 Comparison of acceleration response
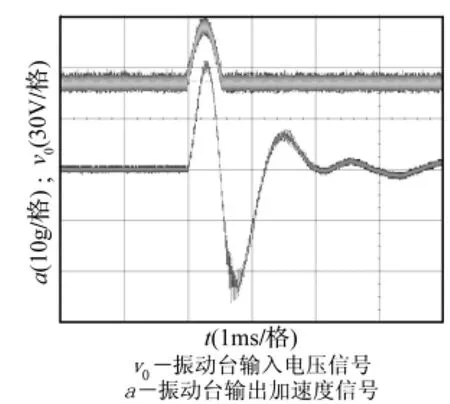
图6 冲击信号输入和输出响应Fig.6 Excitation and response of shock signal
通过系统辨识得到的加速度输出结果与试验测试结果示于图7,其相似度提高为87.29%在所得辨识模型上加载冲击输入信号时,模拟输出与实际输出的相似度为60.57%,最终可判定以冲击信号进行系统辨识所得电动振动台传递函数的参数将更加准确。
冲击信号可以辨识出系统模型原因在于冲击信号的脉宽越窄越接近δ函数,而δ函数是广谱信号,在理论上比人为能得到的随机信号有更宽的频谱,尤其在低频部分,可以更真实地描述系统。而在其它的系统不能使用具有如此多优点的信号进行辨识有两方面原因:① 系统的输出很难跟随上升如此快的冲击信号,因此试验可能导致系统损坏;② 系统的线性区不会无限宽,在含有如此广的频域下会进入非线性区,辨识不出系统的真实模型。
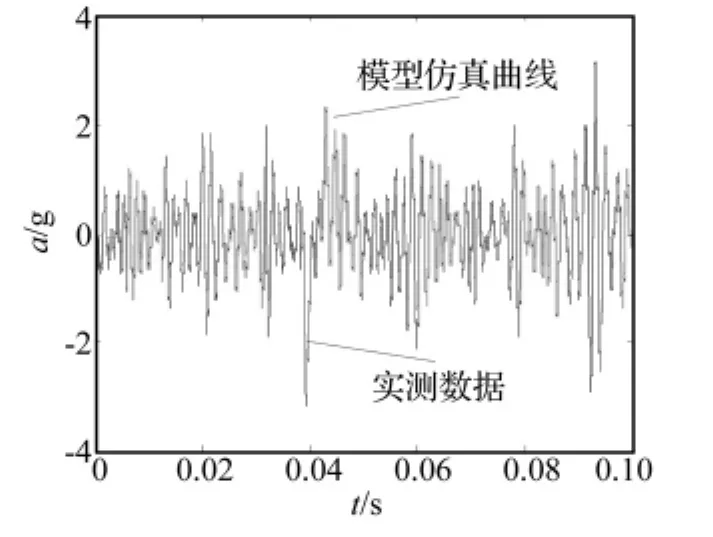
图7 随机仿真输出与实际输出Fig.7 Simulation and test results of random signal
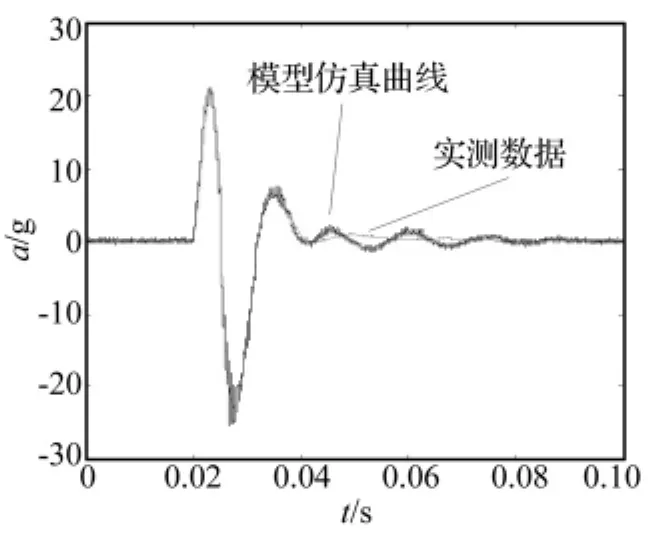
图8 加速度响应结果的比较Fig.8 Comparison of acceleration tesponse
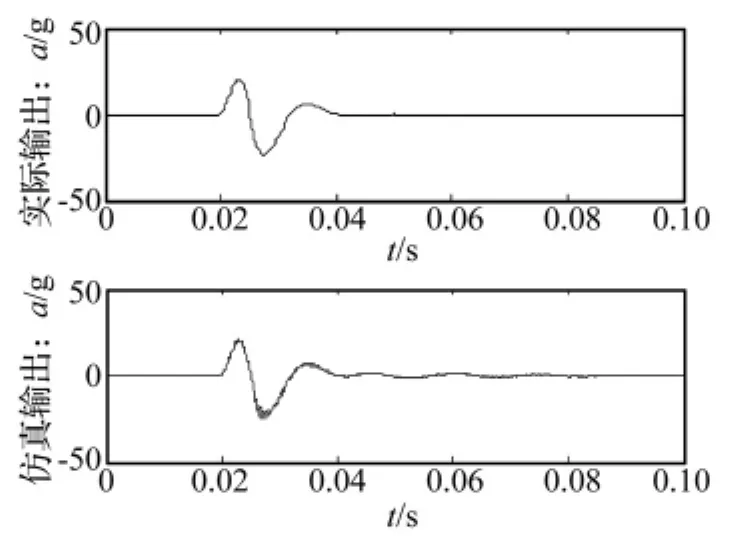
图9 冲击的实际输出和仿真输出Fig.9 Simulation and test output results of shock signal
3.3 传递函数参数估计
为使系统辨识模型更接近真实系统,需进行系统传递函数参数估计。将式(9)中的离散模型转换为连续模型,可得:
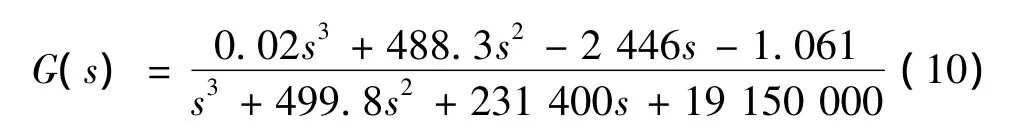
上式与式(6)对应的理论模型零点阶数不符,设定所辨识模型的形式为:
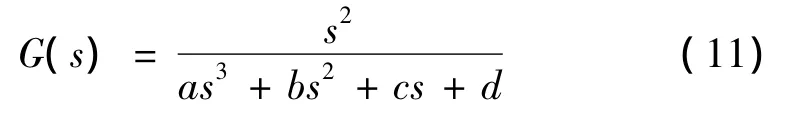
选取 a=1、b=499.8、c=231 400、d=1 915 000 作为变量初值。通过迭代使其收敛于真实模型的参数值,最终所得系统传递函数连续模型G'(s)为:
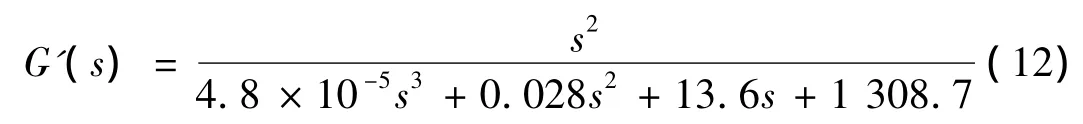
由此得到的振动加速度响应输出测试结果和仿真结果示于图9。参数仿真输出与实际输出相似度高达98.37%,较之前获得的传递函数更加精确。
4 应用实例
文献[8] 中要求的半正弦冲击脉冲试验条件如图10所示。为使振动台产生更大的冲击加速度,通常在冲击前使台面向下产生初速度,如图11中所示A为冲击加速度,kA为向下准备的加速度值,国军标中要求k<0.2,文中k=0.13,这有利于减小振动台受到的直流激励,以免烧毁线圈。同时冲击信号激励振动台时须对信号予以补偿,以保证冲击结束时振动台处于加速度、速度和位移都为零的静止状态。
在MATLAB/Simulink中建立控制系统模型,如图 12所示。信号源Signal3为振动台目标输出激励,返回信号Scope2为振动台加速度响应输出,通过PID反馈控制使输出加速度信号与Signal3一致,则信号 Scope1即为所求的振动台输入激励。当信号源Signal3与返回信号Scope2一致时,可得 PID模型中P=2.9,I=10,D=0。

图10 冲击信号标准波形Fig.10 Standard waveforms of shock signal
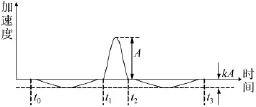
图11 符合国军标要求位移补偿后的波形Fig.11 The displacement compensation waveforms
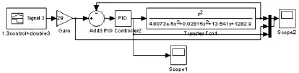
图12 PID仿真模型Fig.12 PID simulation model
试验测试结果如图13所示。产生时间为6 ms的半正弦冲击,之后15 ms产生一负向冲击,使振动台台面在冲击后保持静止,加速度的积分值即振动台台面的运动速度应为零。闭环控制使负向冲击补偿延迟15 ms,从而满足了试验条件要求。

图13 响应输出与信号输入Fig.13 Input and output signal
5 结论
(1)本文提出了一种包括电动振动台系统建模及系统辨识、传递函数参数估计等环节的模型辨识方法。
(2)冲击信号较随机信号而言,具有宽频谱的特点,在低频部分可更加真实地描述系统。因此更适用于电动振动台系统传递函数的辨识。
(3)仿真与试验结果表明,在6ms冲击覆盖的频域下,电动振动台可等价于线性系统,基于振动台传递函数,通过PID仿真控制,实现了振动台规定冲击波形的生成。
[1] 振动与冲击手册编写组.振动与冲击测试技术[M] .北京:国防工业出版社,1990.
[2] 张巧寿.振动试验系统现状与发展[J] .航天技术与民品,2008,8:36 -39.
[3] 刘洪英,马爱军,冯雪梅.冲击响应谱控制系统仿真研究[J] .计算机仿真,2003,20(7):23-25,39.
[4] 袁宏杰,李传日.冲击响应谱控制的研究[J] .北京航空航天大学学报,2000,26(4):494-496.
[5] Chen T H,Liaw C M.Vibration acceleration control of an inverted-Fed electrodynamic shaker[J] . IEEE/ASME Transactions on Mechatronics,1999,4(1):60 -70.
[6] Flora L D,Grundling H A.Vibration acceleration control of an ACpower source-fed electrodynamic shaker[C] .PESC Rec IEEE Annu Power Electron Spec Conf,2005:1175 - 1181.
[7] Han J G,Tang T H,Wang X M.Sinusoidal vibration test control of a switching mode power amplifier-fed electrodynamic shaker[C] .1st IEEE Conference on Industrial Electronics and Applications,2006:1 -5.
[8] GJB360B-2009.电子及电气元件试验方法.

