基于应变和比能双控的钢结构损伤模型
徐龙河,杨冬玲,李忠献
(1.北京交通大学 土木建筑工程学院,北京 100044;2.天津大学 建筑工程学院,天津 300072)
2008年5月12日,我国四川省汶川县发生8.0级特大地震,截至6月18日12时,已造成69176人遇难,受灾人数已达4624万,初步统计损失已达5000多亿人民币[1]。造成这些巨大经济损失和大量人员伤亡的根本原因是地震导致大量房屋倒塌,因此房屋安全问题必须引起高度的重视。如何正确的评价结构的抗震能力及地震过后房屋的剩余承载力,需要建立一个合理的损伤模型以定量计算结构在地震中的损伤指标。损伤指标是用来描述结构、构件或材料受损程度的变量,一般定义为结构或构件反应历程中某一指标累计量与相应指标极限允许量之比,通常用D表示,并且有以下两个特征[2-4]:①损伤指标 D 的范围为[0,1] ,当 D=0时,对应结构的完好状态;当D=1时,意味着结构或构件完全破坏;②损伤指标D为单调递增的函数,即结构的损伤向着增大的方向发展且不可逆。
结构在地震力的作用下产生不同程度的损伤,并且随着荷载循环次数的增加而不断地累积,最终导致结构破坏。合理的损伤模型应能充分体现出大的地震幅值和重复加载效应联合作用导致结构破坏这一事实。比较有代表性的是Park和Wen[5]提出的最大反应变形和累积耗能线性组合的地震损伤模型:
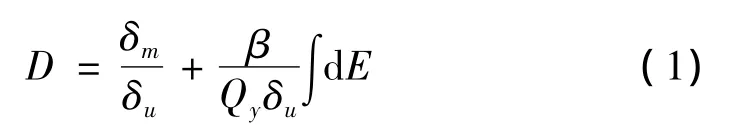
式中,δm和δu分别为结构或构件的最大位移和极限位移,d E为滞回耗能的增量,Qy为结构或构件的屈服强度,β为能量影响系数。
变形和能量双参数损伤模型较好的体现了地震动三要素(幅值,持时和频率)对结构破坏的影响,被学者广泛接受和应用。很多学者在Park-Ang模型的基础上进行改进,提出了很多不同形式的双参数损伤模型。欧进萍等[6]同样采用最大变形与累积耗能的组合,提出了一种适用于钢结构的双参数损伤模型;牛狄涛等[7]指出park模型中变形和能量进行线性组合具有不合理性,提出了变形和能量的非线性组合的双参数损伤模型,并基于实际钢筋混凝土结构的破损分析确定了模型的参数;傅剑平等[8]根据所收集的近十年来国内外完成钢筋混凝土柱的试验结果,对Park-Ang损伤模型进行了识别,对位移贡献和能量项贡献进行了正确的评估,提出了一个更为精确的双参数损伤模型,但暂时只限于柱类构件。
以上的损伤模型是从构件的角度,对Park模型进行改进得到的,同时一些学者突破park模型的形式,从材料的角度提出的损伤模型也被广泛应用。韦未,李同春[9-10]将多轴应力状态下的应变退化得到等效应变,提出了建立在应变空间的混凝土四参数损伤模型。该损伤模型不仅能正确的反映混凝土单轴应力状态下的强度,而且很好的反映多轴应力状态下混凝土的强度。沈祖炎[11]采用塑性应变作为依据,并考虑滞回耗能,提出一个适用于钢构件的损伤模型,并通过低周疲劳试验确定了其中的参数。宋振森[12]把一维应力的损伤理论应用到三维应力,引入等效塑性应变来表征损伤模型,得出了三轴应力下构件的损伤模型。
空间结构受多轴应力的作用,将多轴应力退化得到的等效应力和等效应变可以表征空间结构的受力状态。本文从材料的角度沿用等效应变的思想,并与比能线性组合,提出的损伤模型可以表征三轴应力下结构的损伤变化。
1 应变和比能双控损伤模型
1.1 损伤模型
双参数损伤模型以变形和能量组合的方式很好的体现了结构的破坏机理,本文在此基础上考虑结构空间三向应力的作用,建立了基于等效塑性应变和比能双控的双参数损伤模型:

式中:dj为第j个构件的损伤指标,pi为第i时刻第j构件等效塑性应变;pu为材料的极限等效塑性应变;u为循环过程中产生的累积比能耗散;σy为材料的屈服应力;β为循环荷载影响系数。
其中,钢材的等效塑性应变为:


式中:σi和σi+1分别为第i时刻和i+1时刻的应力,εi和εi+1分别为第i时刻和i+1时刻的应变。
根据 Simo和 Ju[12-13]的分析,延性材料的损伤演化过程可以视为各向同性的,故单向拉伸及循环拉压试验得到的结论在三维应力状态下仍能成立。把应力应变用等效应力和等效应变代替,式(4)可以表征三维应力下的累积比能耗散,即:
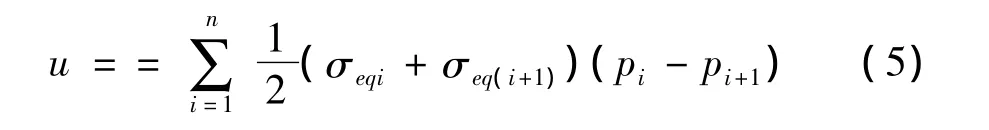
1.2 参数确定
文献[4] 指出从Park模型对破坏构件的计算结果中不难看出,能量项在其中占了很小的份额,对于大多数构件来言,能量项并没有小到可以忽略不计的地步。因此仍有必要在要求较高的抗震设计或评价中使用相对更准确的双参数准则。本文提出的损伤模型以等效塑性应变和比能进行线性组合,β为循环荷载影响系数,也可称为应变项和比能项的组合系数,需要通过试验确定。
Park等人做了261个试验认为混凝土循环荷载影响系数β受剪跨比、轴压比、配筋率和配箍率的影响,一般在 0.3 ~ 0.12 之间,常取 0.15 左右[2,5]。文献[14] 中对欧进萍等人提出的钢结构损伤模型中的参数进行了定义,重要结构取β=2.0,一般结构取为1.0,对位移项和能量项定义了同样的组合系数。这是因为钢结构的耗能能力比混凝土的强,其损伤模型中的能量项占了损伤指标D比较大的份额。
循环荷载作用下,结构的破坏是由首超破坏和累积破坏相互影响的,在钢结构中,其耗能能力更强,故循环荷载对损伤模型的影响更大,所以本文循环荷载影响系数β取为0.3。
1.3 结构层损伤模型
根据构件损伤模型定义如下结构层损伤模型:

式中:Dg为结构层损伤指标,Wj为j构件的损伤加权值,体现了第j个构件在整个结构层中的重要程度。
2 结构损伤程度界定标准
根据震后建筑或构件的破损程度和破坏修复的难易程度,将震害划分为五个等级,即基本完好,轻微破坏,中等破坏,严重破坏和倒塌。由于综合损伤模型可以很好的反映变形和能量对结构的影响,国内外学者在各自所提出的损伤模型的基础上进一步划分结构的震害等级,确定了结构的模糊安全准则。本文的损伤模型是从等效塑性应变角度提出的,当结构处在弹性阶段时,塑性应变为0,此时的损伤指数为0,在此不考虑结构在弹性阶段的损伤,即假定结构处在弹性变形阶段时是完好的。参考《中国地震烈度表》中给出的震害指数及文献[17] ,并结合本损伤模型的特点,定义了对应结构不同破坏等级的损伤指数范围。表1为国内外学者损伤模型和本文损伤模型不同的震害等级对应的损伤指标范围。

表1 不同震害等级对应的损伤指标范围Tab.1 Ranges of damage index corresponding to different damage grades
3 数值算例
3.1 有限元模型
为了验证本文所提出的损伤模型的正确性和实用性,采用 9层 Benchmark结构模型[18],对其输入 El Centro波,进行倒塌数值模拟分析。该结构平面尺寸为45.73 m ×45.73 m,X、Y 方向各五跨,每跨宽 9.15 m;原结构地上九层,地下一层,本文只取地上部分进行建模。首层层高为5.49 m,标准层层高为3.96 m。结构的总体质量为9×106kg。模型立面图如图1所示。梁柱均采用H型钢,截面尺寸如表2所示。柱的屈服强度为345 MPa,梁的屈服强度为248 MPa,采用与应变率有关的塑性随动强化材料模型,通过Cowper—Symonds方程考虑应变率对屈服应力的影响[19]。采用有限元软件LS-DYNA建模分析,利用空间梁单元模拟梁柱构件,板单元模拟楼板,有限元模型如图2所示。分别输入2倍,3倍,5倍,6倍,7倍的双向 El Centro波,持续时间为20s。El Centro加速度时程曲线如图3所示。

图1 9层benchmark模型结构立面Fig.1 Elevation of 9-story benchmark model structure

图2 有限元模型Fig.2 Finite element model

图3 El Centro波加速度时程曲线Fig.3 Time histories of El Centro earthquake records

表2 梁柱截面尺寸Tab.2 Sizes of beam and column
3.2 结果分析
图4为5倍El Centro波下柱子损伤指标时程曲线。对比各个时刻角柱,边柱和中柱的损伤演化值,可以看出不同位置的柱子损伤发展过程有相同的规律。在2 s之前柱子处在弹性阶段,此时的损伤为0;在2.6 s和11.4 s时,损伤突然增大,因为南北向和东西向的El Centro地震波加速度值在这两个时刻分别达到了最大值;随着地震波强度的加大和时间的延长,损伤逐渐累积,结构的损伤向着增大的方向发展且损伤不可逆,曲线单调递增,这与损伤指标特征的第二项是一致的。对比同时刻不同位置柱子的损伤可以看出,角柱的损伤大于边柱,边柱的损伤大于中柱,与结构在双向地震中角柱受力最大,其次为边柱,中柱受力相对较小相一致。

图4 5.0倍El Centro地震动下柱子损伤发展过程Fig.4 Damage evolution process of columns under the excitation of 5.0 times El Centro earthquake
表3是地震波持续时间内4个主要时刻柱子的损伤值和一至三层层间损伤值的变化率。从表上可以清晰的看出,同一时刻底层柱的损伤值较大,层数越高损伤值越小。框架结构以剪切变形为主,并且首层较高,形成薄弱层,在地震波作用结束时,底层柱破坏最为严重,损伤指数达到了0.450 7,对照不同震害等级对应的损伤指标范围表1,此时柱子已经严重破坏。从柱层间损伤值变化率上来看,当构件损伤值达到最大的时刻,3层相对2层的损伤值变化率小于2层相对1层的,说明框架结构层数越高柱损伤程度变化越小。

表3 主要时间步柱的损伤值和层间损伤值变化率Tab.3 Column damage value and inter-story damage variation rate at main time steps
图5为5倍、6倍和7倍El Centro地震输入时结构首层损伤指标变化曲线。从中看出,结构层的损伤与柱子的损伤发展有相同的规律,即结构先是处在弹性阶段,随着地震强度的加大和地震波持续时间的增长而损伤增大。地震强度不同,结构开始产生损伤的时间不同。在输入的双向地震波分别达到其峰值加速度时,结构层的损伤指标发生了一个突然增大的过程,并且在第二个地震加速度峰值到达时,6倍和7倍El Centro波下结构层的损伤指标达到了0.5,结构很快发生倒塌倾覆。

图5 不同地震强度下首层损伤发展过Fig.5 Global damage evolution process of the first floot under different earthquake intensity
图6 为不同地震强度下结构首层的层间位移时程曲线图,表4为不同强度地震动下结构层的损伤指标和最大的层间位移角。地震动强度为2倍El Centro波时,最大的层间位移角为0.013,结构层的损伤指标达到了0.087,对照本文模型不同的损伤程度对应的损伤指数范围表,此时结构发生了轻微的破坏;在地震动强度为3倍El Centro波时,图6(a)中的层间位移曲线围绕平衡位置上下摆动,此时的层间位移角达到了0.02左右,损伤指标也达到了0.18,对照表1,结构发生了中等破坏;地震动强度为5El Centro波时,层间位移角达到了0.093,明显超过了我国抗震设计规范规定的钢框架结构弹塑性层间位移角1/50的限值,图6(b)中层间位移也明显增大,X、Y向的层间位移偏离平衡位置,达到最大值后围绕最大值上下波动,说明变形未达到其破坏临界条件,结构未发生倒塌倾覆,此时结构的损伤指数为0.34,对照表1本文模型不同的损伤程度对应的损伤指数范围,已经严重破坏;图6(c)和图6(d)中,地震动强度分别为6倍和7倍的El Centro波,层间位移曲线持续增大最后趋于发散,结构层的损伤指标大于0.5,说明结构已经完全倒塌。

表4 不同地震强度下结构损伤指标和层间位移角Tab.4 Global damage and inter-story drift angle at different earthquake intensity
4 结论

图6 不同地震强度下层间位移时程曲线Fig.6 Time history responses of relative displacement at different intensity of El-Centro earthquakes
本文从材料的角度,综合考虑结构在地震中的破坏机理,提出了一个基于等效塑性应变和比能双控的双参数损伤模型,并在在前人试验和理论分析的基础上,参考我国抗震烈度,结合本文损伤模型的特点,定出了结构不同破坏程度对应的损伤指标范围。结合一9层benchmark模型结构应用该损伤模型对其在El Centro波作用下的倒塌过程进行了数值模拟分析,结果表明随着地震强度的加大和地震波持续时间的增长结构层的损伤与柱子的损伤增大,地震强度不同,结构开始产生损伤的时间不同。在输入的双向地震波分别达到其峰值加速度时,结构层的损伤指标发生了一个突然增大的过程,并且在第二个地震加速度峰值到达时结构很快发生倒塌倾覆。验证了该损伤模型评估强震下钢结构竖向构件及层的损伤发展过程的有效性。
[1] 李宏男,肖诗云,霍林生.汶川地震震害调查与启示[J] .建筑结构学报,2008,29(4):10 -19.
[2] 张永鑫,凌 煜,张 熠.双参数地震损伤模型综述[J] .山西:山西建筑,2009,35(27):64 -65.
[3] 董 宝,沈祖炎.空间钢构件考虑累积损伤累积效应的恢复力模型及试验验证[J] .上海力学,1999,20(4):341-347.
[4] 李翌新,赵世春.钢筋混凝土及劲性钢筋混凝土构件的累积损伤模型[J] .四川:西南交通大学学报,1994,29(4):412-417.
[5] Park Y J,Ang A.Mechanistic seismic damage model for reinforced concrete[J] .Journal of Structural Engineering,ASCE,1985,111(4):740 -756.
[6] 欧进萍,牛获涛,王光远.多层非线性抗震钢结构的模糊动力可靠性分析与设计[J] .地震工程与工程震动,1990,10(4):27-37.
[7] 牛狄涛,任利杰.改进的钢筋混凝土结构双参数地震破坏模型[J] .地震工程与工程振动,1996,16(4):44-54.
[8] 傅剑平,王 敏,白绍良.对用于钢筋混凝土结构的Park-Ang双参数破坏准则的识别和修正[J] .地震工程与工程振动,2005,25(5):73 -79.
[9] 韦 未,李同春.一种新的用于各向同性损伤模型的四参数等效应变[J] .工程力学,2005,22(6):91 -96.
[10] 韦 未,李同春,姚纬明.建立在应变空间上的混凝土四参数破坏准则[J] .水利水电科技进展,2004,24(5):27-29.
[11] Shen Z Y,Dong B.An experiment-based cumulative damage mechanics model of steel under cyclic loading[J] .Advance in Structural Engineering,1997,1(1):39-46.
[12] 宋振森.超高层钢结构考虑损伤和损伤累积的分析方法[D] .上海:同济大学,2003.
[13] Ju J W.Strain-and stress-based continum damage models-I:formulation[J] . International Journal of Solids and Structures.1987,23(7):821 -840.
[14] Simo JC,Ju,JW.Strain-and stress-based continum damage models-II:computational aspects[J] .International Journal of Solids and Structures.1987,23(7):841 -869.
[15] 陈树勋,王光远.工程结构与系统抗震优化设计的实用方法[M] .北京:中国建筑工业出版社,1999.
[16] 刘海卿,陈小波,王学庆.应用损伤指数的框架结构倒塌数值模拟分析[J] .自然灾害学报,2008,17(5):21 -25.
[17] 姚谦峰,苏三庆.地震工程[M] .陕西:陕西科学技术出版社,2001.
[18] Ohtori Y,Spencer Jr B F,Dyke S J.Benchmark control problems for seismically excited nonlinear buildings[J] .Journal of Engineering Mechanics,ASCE,2004,130(4):366-385.
[19] LS-DYNA.Keyword user's manual[M] .Livermore,California:Livermore Software Technology Corporation,2006.

