一类带有混合约束的二次半定规划及其投影收缩算法
田朝薇,宋海洲
(华侨大学数学科学学院,福建泉州362021)
一类带有混合约束的二次半定规划及其投影收缩算法
田朝薇,宋海洲
(华侨大学数学科学学院,福建泉州362021)
研究带有线性等式及线性不等式约束的二次半定规划问题.讨论对偶理论、最优性条件及其等价的单调变分不等式,给出相应的投影收缩算法.经收敛性分析,可得该算法是全局收敛的.
二次半定规划;投影方程;变分不等式;投影收缩算法
半定规划在系统论、控制论、组合优化、特征值优化等诸多领域中有着广泛的应用,而且它有行之有效的多项式时间算法.目前,研究较多的是在满足约束对称矩阵的仿射组合半正定的条件下,使线性函数极小化,即线性半定规划问题[1-3].在文[4]给出的求解半定规划的二次摄动方法中,其摄动问题的对偶规划可转化为一个只有变量半正定约束的二次半定规划问题(QSDP).文[5]在文[4]基础上加以等式约束进行讨论.本文在文[5]的基础上加上不等式约束,讨论对应的投影收缩算法.
1 二次半定规划问题
考虑二次半定规划问题,即
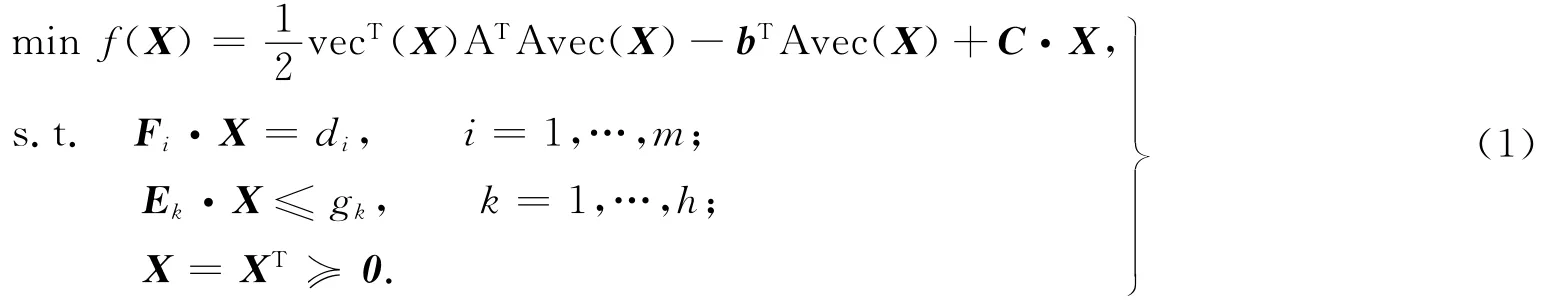
式中:C,X均为n阶实对称矩阵;vec(X)表示由矩阵X的列叠成的n2维列向量,并且Rl×n2;Aj(j=1,…,l);Fi(i=1,…,m);Ek(k=1,…,h);b∈Rl;d∈Rm;g∈Rh;X≥0表示矩阵X是半正定的.A·B=∑i,jAi,jBi,j=tr(ATB),矩阵运算A·B的定义为矩阵A,B的内积,tr为矩阵的迹.
假设Fi(i=1,…,m)线性独立,对于问题(1),因为ATA是对称半正定的,其目标函数是一个凸二次函数,而且矩阵的半正定约束也是凸的.因此,式(1)是一个凸二次优化问题.
2 对偶理论
若引入拉格朗日乘子λ∈Rm,μ∈Rh,Z=ZT∈Rn×n,且μ≥0,Z≥0,则二次半定规划(1)的拉格朗日函数为

易知,式(2)也是一个二次半定规划问题,其目标函数为拉格朗日函数L(X,λ,μ,Z)在可行域上的简化.
引理1[1]设A和B是两个n阶实对称矩阵,若A≥0,B≥0,则A·B≥0.
由凸规划的对偶理论,有如下的弱对偶定理.
定理1 设X为二次半定规划问题(1)的可行解,X,λ,μ,Z为对偶问题(2)的可行解,则有

证明 设Y为二次半定规划(1)的可行解,X,λ,μ,Z为对偶问题的(2)的可行解.由f(X)的凸性,得∀X,Y∈D,则
D={X=XT∈Rn×n|Fi·X=di,i=1,…,m;Ek·X≤gk,k=1,…,h;X≥0}
为问题(1)的可行域,有

3 投影收缩算法
在问题(1)的不等式约束中加入松弛变量γ∈Rh且γ≥0,则式(1)变为


设S={X∈Rn×n|X=XT≥0}为n阶实对称半定矩阵的集合.
引理2[1]设A∈S,B∈S,则A·B=0当且仅当AB=0.
引理3[6]若A∈S,B∈S,则AB=0当且仅当E(A)=0.其中:E(A)=A-PS[A-B],PS表示到S上的正交投影.
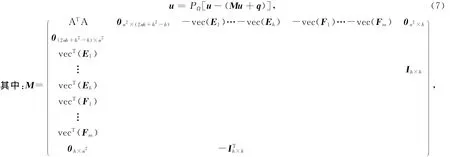
由引理2,3可知,最优性条件(6)等价于投影方程[6],即S(n+h)×(n+h)×R(m+h),Ih×h为h阶单位矩阵.因为M半正定,所以投影方程(7)实际是一个单调线性投影方程.由文[7]可知,方程(7)与变分不等式

等价.其中:u*∈Ω*,Ω*为投影方程(7)的解集合.因此,变分不等式(8)是单调线性变分不等式,可利用投影收缩算法求解二次半定规划问题(4).
另外,对于β>0和任意的u∈Ω[4],有

其分别与式(8)和式(7)等价.
下面给出求解单调线性变分不等式(8)的投影收缩算法.
给定初始点μ0∈Ω,参数β>0和要求的精度ε>0,则有如下3个步骤.
(1)方向和步长可按如下3种方法选择:
(a)当Q=I时,有
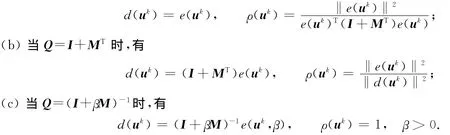
其中:e(uk,β)=uk-PΩ[uk-β(Muk+q)],e(uk)=e(uk,1),即迭代过程中投影方程的偏差.
(2)迭代格式为
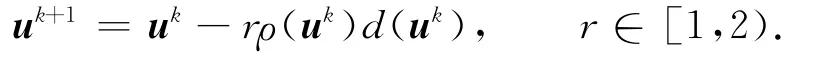
(3)停止准则.对给定精度ε>0,当‖e(uk)‖≤ε时,算法停止.
4 算法的收敛性分析


[1] HELMBERG C.Semidefinite programming for combinatorial optimization[M].Berlin:Konrad-Zuse-Zentrum for Information Stechnik,2000.
[2] VANDENBERGHE L,BOYD S.Semi-definite programming[J].SIAM Review,1996,38(1):49-95.
[3] ALIZADEH F.Interior point methods in semi-definite programming with application to combinatorial optimization[J].SIAM J on Optim,1995,5(1):13-51.
[4] 韩乔明.解半定规划的二次摄动方法[J].应用数学学报,1999,22(1):84-90.
[5] 关秀翠,刁在筠.二次半定规划问题及其投影收缩算法[J].高等学校计算数学学报,2002,6(2):97-108.
[6] HAN Q.Projection and contraction methods for semi-definite programming[J].Appl Math Compute,1998,95(2/3):275-289.
[7] HARKER P T,PANG J S.Finite dimensional variational inequality and nonlinear complementary problems:A survey of theory algorithms and applications[J].Mathematical Programming,1990,48(1/2/3):161-220.
[8] HE B.Solving a class of linear projection equations[J].Numer Math,1994,68(1):71-80.
[9] HE B.A new method for a class of linear variational inequalities[J].Math Programming,1994,66(2):137-144.
A Class of Quadratic Semi-Definite Programming with Mixed Constraints and Its Projection and Contraction Algorithm
TIAN Zhao-wei,SONG Hai-zhou
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)
In this paper,we discuss a class of quadratic semi-definite programming problem with linear inequality constraints and linear inequality constraints.The duality theories are presented.After proving the equivalence of its optimality conditions and monotonous linear variational inequalities,we present its projection and contraction algorithm.It is proved that the algorithm is global convergence after analyzing its convergence.
quadratic semi-definite programming problem;projection equation;variational inequalities;projection and contraction algorithms
O 221.2
A
(责任编辑:陈志贤 英文审校:张金顺,黄心中)
1000-5013(2011)01-0113-05
2009-01-04
田朝薇(1977-),女,讲师,主要从事运筹与优化的研究.E-mail:tzhw@hqu.edu.cn.
福建省自然科学基金资助项目(Z0511028)

