广义Logistic型泛函微分方程零解的全局吸引性

汪东树，王全义

（华侨大学数学科学学院，福建泉州362021）

广义Logistic型泛函微分方程零解的全局吸引性

汪东树，王全义

（华侨大学数学科学学院，福建泉州362021）

研究广义Logstic型泛函微分方程x′（t）＋［1＋x（t）］F（t，x［·］α）＝0（t≥0，α≥1）零解的全局吸引性.运用一些分析方法和技巧，对该方程的零解作出估计，得到方程零解是全局吸引的一些充分条件，结果推广并改进了现有文献中的相关结论.

广义Logistic型泛函微分方程；全局吸引性；振动；非振动

1 基本定理和引理

令g∶［0，＋∞）是一个非减的连续函数，且满足g（t）＜t，t≥0，以及g（t）→＋∞（t→＋∞）.对于任意t≥0，用Ct表示连续函数φ∶［g（t），t］→［－1，＋∞）的全体构成的赋范空间，其范数定义为

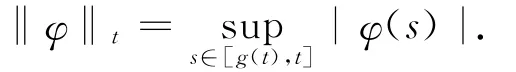
文［1］研究一维Logstic型泛函微分方程

零解的全局吸引性.式（1）中，F（t，φ）是［0，＋∞）×Ct上的连续泛函，F只依赖于t和φ在［g（t），t］上的数值，F（t，0）≡0，t≥0，且满足Yorke条件为

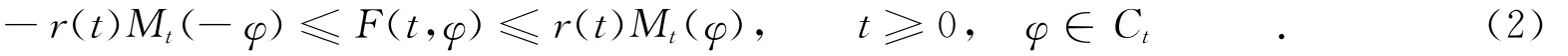
其中，Mt（φ）＝max｛0，ss［u（p

t），t］φ（s）｝，r（t）∈C（［0，＋∞），（0，＋∞））.令τ＝－g（0），则式（1）相应的初始

∈g条件为

式（3）中，φ∈C（［－τ，0］，［－1，＋∞）），φ（0）＞－1.文［1］得出如下的定理.

定理A 假设式（2）成立，且对于每个ε＞0，存在η＝η（ε）＞0，使得如果infφ（s）≥ε，就有

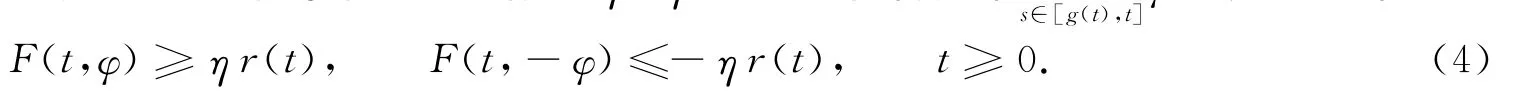
如果还满足

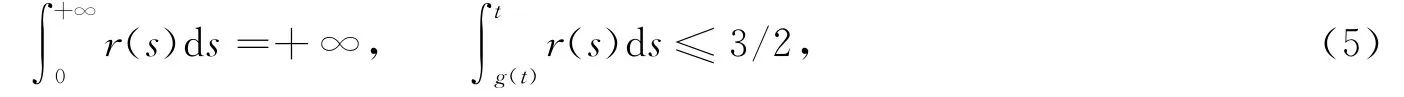
对于充分大的t，式（1），（3）的每个解趋于零.

容易看到，对于广义时滞Logistic方程

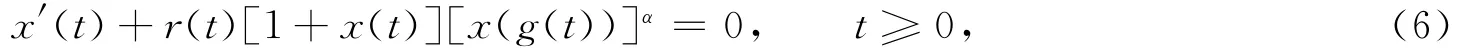
F（t，φ）＝r（t）［φ（·）］α并不满足条件（2）.其中，α≥1为两正奇数之比，r（t），g（t）同前.因此，方程（6）零解的全局吸引性问题应另行研究.文［2－3］研究了式（6）在初始条件式（3）下的零解的全局吸引性问题.文［4］研究了包括式（1），（6）在内的更一般性的泛函微分方程，即

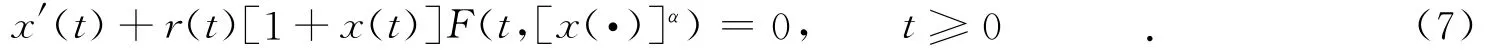
2 主要结果和证明

且不等式组

定理1 在引理2成立的条件下，若式（5）成立，并满足条件

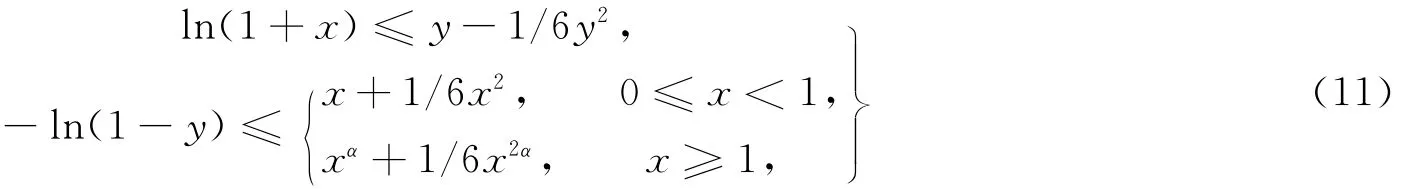
在区域D＝｛（x，y）∶x≥0，0≤y＜1｝内只有唯一解（x，y）＝（0，0），则式（3），（7）的每个解趋于零.

证明 设x（t）＝x（t，0，φ）是式（3），（7）的解.由引理1可知，x（t）在［0，＋∞）上存在且满足对一切t≥0，有x（t）＞1.由引理2可知，若x（t）为非振动解时，有

成立.因此，只需讨论x（t）为振动解的情形.

首先证明，若x（t）为振动解，则x（t）有界.

令t1＞0，使得当t≥t1时，有g（t）≥0.令t＊（t＊＞t1，t＊充分大）是x（t）的任一个局部左极大值点，且x（t＊）＞0.显然，有x′（t＊）＝0.由式（8）可知，F（t＊，［x（·）］α＝0.下面证明存在t0∈［g（t＊），t＊］，使得x（t0）＝0；否则，由前面假设可知，当t∈［g（t＊），t＊］时，有x（t）＞0.由于x（t）是振动解，由闭区间上的连续函数介值性定理，可知存在t＊＊＜g（t＊）（g（t＊＊）＞0），使得x（t＊＊）＝x（g（t＊））／2，且当t∈［t＊＊，g（t＊）］时，有x（t）＞0.因此，由式（2）可知，当t∈［t＊＊，g（t＊）］时，有F（t，［x（·）］α）≥0.

方程（8）两端从t＊＊积分至g（t＊），有

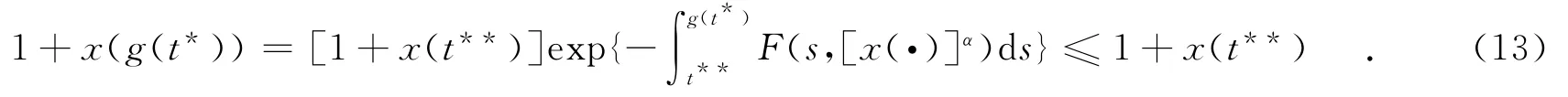
这与假设x（t＊＊）＝x（g（t＊））／2相矛盾.即存在t0∈［g（t＊），t＊］，使得

方程（7）两端从t0积分至t＊，可得

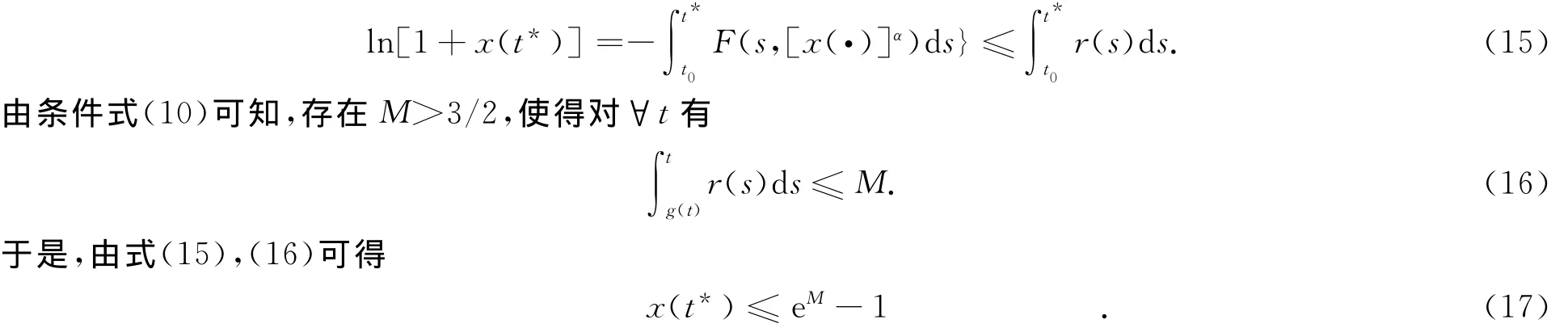
其中，可设t＊充分大.由于t＊的任意性，即证明了最终有x（t）≤eM－1.

令¯t（¯t＞t1）是x（t）的任一个局部左极小值点，且x（¯t）＞0.显然，有x′（¯t）＝0.类似于式（14）的证

于是，可得到如下的结论.

推论1 当α＝1时，在定理1成立的条件下，且式（5），（10）成立，则式（1），（3）的每个解趋于零.推论1比定理A的结果要好，包含了目前关于α＝1的很多结果［5］.

［1］ 庾建设.一类泛函微分方程零解的全局吸引性及应用［J］.中国科学：A辑，1996，26（1）：23－33.

［2］ CHEN M，YU J，ZENG D，et al.Global attractivity in a generalized nonautonomous delay Logistic equation［J］.Bulletin of Institute of Mathematics Academia Sinica，1994，22（2）：91－99.

［3］ LI Jing－wen.Global attractivity in a generalized delay Logistic equation［J］.Applied Mathematics：A Journal of Chinese Universities（B），1996，11（2）：165－174.

［4］ 王晓萍，廖六生.广义Logistic型泛函微分方程零解的全局吸引性［J］.应用数学学报，2004，27（1）：172－179.

［5］ 唐先华，庾建设.Logistic型脉冲泛函微分方程零解的全局吸引性［J］.数学学报，2002，25（5）：941－952.

Global Attractivity of the Zero Solution of the Super Logistic Functional Differential Equations

WANG Dong－shu，WANG Quan－yi
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

In this paper，the super Logistic type functional differential equations is investigated x′（t）＋［1＋x（t）］F（t，x［·］α）＝0，t≥0，α≥1.By using some analysis methods and techniques，some sufficient conditions are obtained for global attractivity of the zero solution by means of eatimating zero solution of the equation.The reference is generalized.

super Logistic type functional differential equations；global attractivity；nonoscillation；oscillation

O 175.12；O 175.15

A

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

1000－5013（2011）01－0103－06

2009－05－03

汪东树（1981－），男，讲师，主要从事常微分及泛函微分方程的研究.E－mail：wangds＠hqu.edu.cn.

福建省自然科学基金资助项目（Z0511026）；国务院侨办科研基金资助项目（09QZR10）