优化设计在PDC残余热应力计算中的应用

张 菁，黎明发，孙振亚，范 端，吴 波

(1.武汉理工大学机电工程学院，湖北 武汉 430070;2.武汉理工大学高温高压物理研究所，湖北 武汉 430070)

聚晶金刚石复合片(polycrystalline diamond compact，PDC)是由聚晶金刚石(polycrystal-line diamond，PCD)层与硬质合金基体构成的超硬复合材料。PDC是在高温、高压(1300～1500℃、6 GPa)条件下由金刚石微粉与硬质合金基体烧结而成，由于金刚石与硬质合金的热膨胀系数相差太大，在卸压冷却过程中，PDC容易在界面产生很大的残余热应力［1-2］。残余热应力的存在使PDC强度降低，尤其在承受较高外力或温度变化较大时，PCD层容易破损或从基体上剥落，导致失效［3-4］。因此，研究PDC残余热应力具有非常重要的意义，且应用优化方法对PDC进行残余热应力计算是十分必要的。

常见的一种PDC残余应力计算方法是应用ANSYS软件进行，但对某一种有限元模型来说，当需要修改设计时，就必须修改有限元模型的几何尺寸或载荷状况，建立新的有限元模型，然后再重复分析计算过程。这种“设计—分析—修改设计—再分析—再修改”的过程，在有限元分析中存在大量重复性的工作，直接影响设计效率。运用ANSYS提供的ANSYS参数化设计语言APDL(ANSYS parametric design language)，并通过使用APDL语言编写的命令流，可自动完成上述循环计算功能，大大方便了建模、计算与数据处理。采用参数化建模及基于APDL语言的程序编写，弥补了ANSYS在该方面专业性不强的缺陷。

1 ANSYS优化原理及优化方法

1.1 优化模型的建立

优化问题的基本原理是在建立优化模型的基础上，运用各种优化计算方法，在满足设计要求的条件下迭代计算，求得目标函数的极值，得到最优设计方案。

一般优化问题的数学模型可表示为［5-6］:

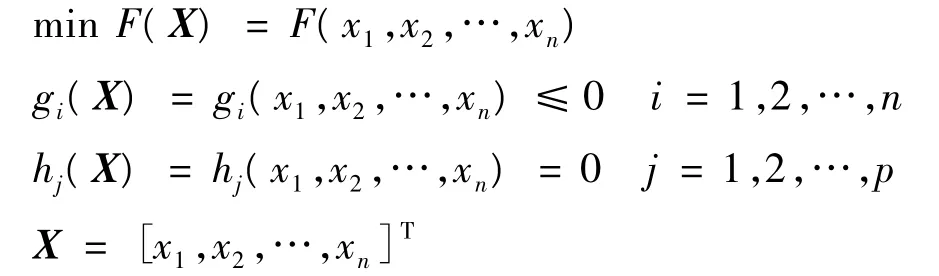
F(X)为目标函数，用于评价设计方案的优劣，设计问题即为求目标函数的极值。gi(X)、hj(X)为约束条件，即设计变量取值范围及状态变量在空间范围的限制条件，是设计变量的函数。X为设计向量，由设计变量构成，是设计中需优选的设计参数，每个设计向量即为一个设计方案，设计向量的集合即为设计空间，满足约束条件的设计向量的集合为可行域。

为了将有限元与优化方法结合，可以采用曲线拟合的方法形成目标函数及状态变量的近似函数表达式，目标函数与状态变量均可采用如下形式的拟合曲面方程:

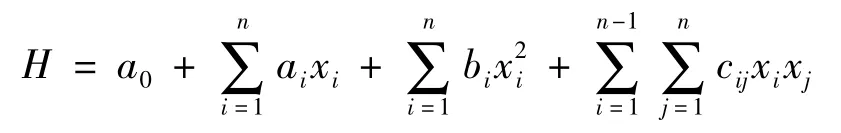
加权最小乘误差为:

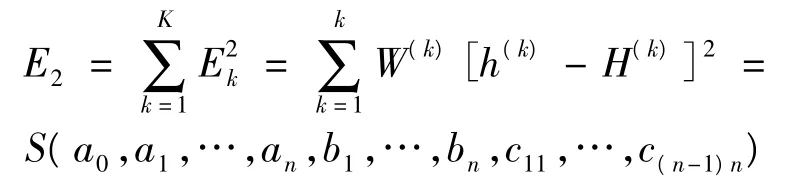
K为设计变量的组数，h(k)为由有限元法计算出的第k组设计变量对应的H值，H(k)为由近似算法得出的第k组设计变量下的H值，W(k)为第k组设计变量的权，其值可根据第k组设计变量与当前最小目标函数对应的设计变量的设计空间距离及目标函数值确定。

根据最小二乘法原理，求E的极小值，得正则方程组为:

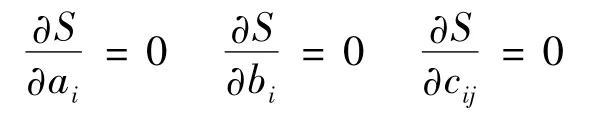
解上述方程即可得 ai，bi，cij，由此拟合目标函数及状态变量，采用各种优化方法，通过优化迭代，可得出目标函数的极值。

1.2 PDC优化结果分析方法

不同的载荷可能会激发不同的残余应力，使之成为主要的破坏因素，考虑PDC抗冲击性或耐磨性的不同性能，残余应力优化结果是不同的。在分析PDC残余应力时不能单从某一个应力上得到该应力数值下的残余应力结果更好或是单从残余应力这一个方面来分析残余应力对PDC性能的影响。因此要考虑PDC的使用性能，PDC是焊接在何种钻头上，在钻进过程中PDC的受载情况，不同的受载情况下PDC更易产生哪种应力为主导的破坏等，在某些条件下才能了解哪种径厚比下的残余应力更有利于PDC的性能。

考虑上述因素，再次假设综合残余应力C，c为影响各残余应力大小的因子，f为残余应力。公式C=c1f1+cyfy+cxyfxy-cxfx表示各种因素下PDC残余应力大小。其中:c1为第一主应力影响因子;cy为最大轴向拉应力影响因子;cxy为最大切应力影响因子;cx为最大径向压应力影响因子;f1为第一主应力;fy为最大轴向拉应力;fxy为综合残余应力;fx为最大径向压应力。

f1、fy、fxy是对PDC使用性能有害的残余应力，而fx是对PDC承受更大的载荷有利的残余应力，因此它们前面的正负号符合这一规律。c1、cy、cxy、cx的大小要考虑的因素众多且不确定，因此，上述公式需要在对PDC、钻头工作情况及规律有更深入的了解时才有更明确的指导意义。

2 平面界面PDC几何参数优化

2.1 前后处理及提取参数化结果

用设计变量作为参数建立模型的工作是在PREP7中完成的。在优化模型中，选择常用的13 mm×8 mm平面界面PDC，将PCD层与硬质合金层厚度比及PDC径厚比作为设计变量。对原始模型作适当简化，在ANSYS里建立起参数化模型，如图1(a)所示。由于PDC的轴对称性，有限元模拟过程中仅选用1/4模型进行计算。

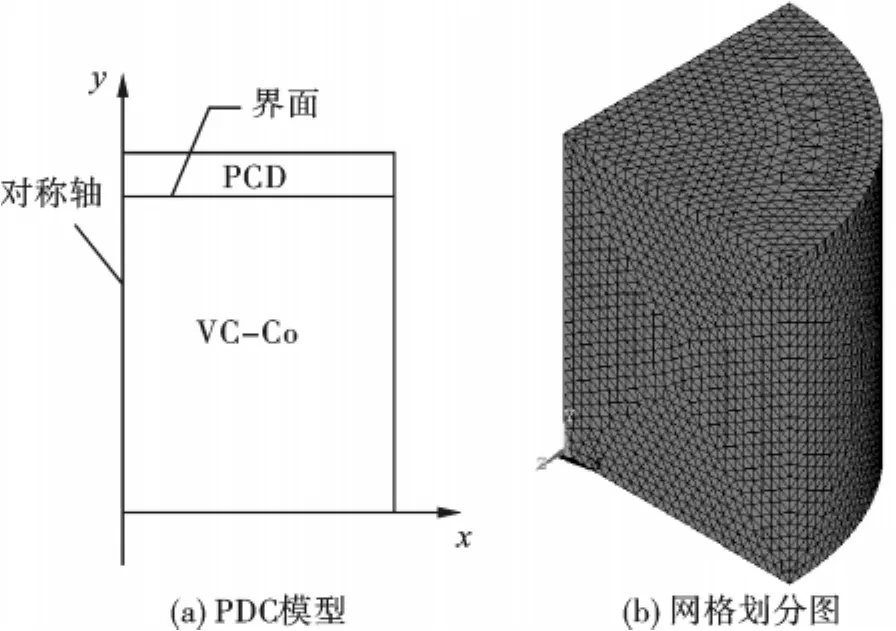
图1 PDC模型及网格划分图

采用SOLID70三维实体热单元，利用间接法进行残余热应力分析。在进行热分析后，将SOLID70转换为相对应的三维实体结构单元，利用体的节点温度作为体载荷进行结构分析［7］。建立有限元模型并划分网格如图1(b)所示。运用ANSYS软件，利用“热-结”耦合法进行残余热应力分析，设定1000℃为PDC应力松弛温度，在这一温度以上PDC的残余热应力可忽略不计，室温为20℃。

按照正常的步骤定义单元类型和材料性质，划分网格，施加载荷，完成有限元计算。然后在POST1中提取结果并赋值给相应的参数，该参数一般为状态变量和目标函数。对于PDC，分别提取最大径向压应力、最大轴向应力、最大剪应力和第一主应力作为其残余热应力主要参考因素。进入优化处理器OPT并指明分析文件，将PCD层与硬质合金层厚度比H及PDC径厚比T作为设计变量，将最大径向压应力、最大轴向应力、最大剪应力和第一主应力作为目标函数，并确定各参数的变化范围。选用零阶方法和等步长搜索法控制参数的优化方式，执行优化分析。

2.2 优化结果分析

计算结果如图2所示，PCD层上的最大径向压应力出现在PDC界面结合处，研究表明它对PDC在钻进时抵抗外力是有利的［8］;最大轴向应力位于PCD层外缘平行于界面处，易导致PDC层的碎裂或脱层;最大剪应力同样位于界面边缘，当它超过PCD层与硬质合金基体间的结合力时，将导致脱层;第一主应力(即最大拉应力)出现在靠近界面边缘处且平行于界面，大大减少了PDC在使用中能承受的载荷大小，特别当PDC承受侧边冲击时极易造成裂纹或脱层。

图2 应力计算结果界面图

2.2.1 PCD层与硬质合金层厚度比的优化结果

不同PCD层与硬质合金层厚度比下的优化结果如图3所示。假设PDC的厚度不变，随着PCD层与硬质合金层厚度比的增加，PCD层的第一主应力呈上升趋势，并且在厚度比为0.17和0.30处出现极小值;径向最大压应力逐渐下降且下降速率减小，从厚度比接近0.20开始基本保持不变;最大轴向拉应力随着厚度比的增加而呈上升趋势，并且在厚度比为0.13～0.17处出现平台阶;最大剪切应力随着厚度比增加从正值变为负值，在厚度比为0.07处为0 Pa，在厚度比为0.17处出现极小值。

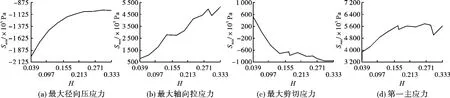
图3 PCD与硬质合金层厚度比的优化结果

从图3可看出，PCD与硬质合金层厚度比越小对PDC的性能和使用寿命越有利，徐国平［9］等亦通过研究提出:PCD层薄的PDC抗冲击性更好，但较薄的PCD层会影响PDC的使用寿命，PCD层与硬质合金层厚度比值应存在一个最佳值。综合图3和图4的分析结果可知，PCD与硬质合金层的最佳厚度比为0.17。

2.2.2 PDC径厚比的优化结果分析

PDC径厚比的优化结果如图4所示。从图4可以看出:假设PDC的厚度不变，随着PDC径厚比的增加，PCD层第一主应力有多个极小值，在径厚比约为 0.76、0.90、0.97、1.10、1.23 等处;径向最大压应力逐渐增大，对PDC界面结合及承受最大载荷越有利;最大轴向应力的多个极小值在径厚比约为0.70、0.80、0.84、0.90、1.10 等处;最大剪切应力的多个极小值在径厚比约为0.76、0.90、1.10、1.17等处。在上述各点处PDC性能越好，出现微裂纹的可能性就越小。

从不同的残余应力考虑，可以得到不同的径厚比最佳值，但是不同的残余应力得到的结论有时是矛盾的。如以第一主应力为主要考虑因素，则在PDC径厚比为0.77时，PDC层第一主应力最小，但是最大拉应力及最大剪切应力则在这个径厚比时是极大值，最大径向压应力也不尽如人意，因此不能简单地说在哪一径厚比最佳。

残余应力本身的存在会使PDC的性能下降，严重的会产生微裂纹，但是更多的是PDC在使用过程中受压力和冲击载荷而破坏。因此要分析出PDC哪种残余应力是破坏的主要因素还需了解PDC在使用中的情况。

3 结论

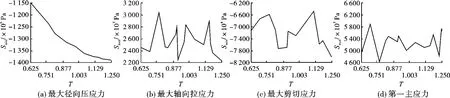
图4 PDC径厚比的优化结果

(1)采用优化方法计算PDC残余热应力能够简化计算步骤提高计算速率，并且计算结果较原来运用单纯取点计算更精确。

(2)从上述优化结果分析可知，考虑PDC抗冲击性能可取PCD与硬质合金层厚度比为0.17为最佳值，但从各个残余应力来说不能简单地下结论哪一径厚比最佳。

(3)考虑不同情况下各因素对残余应力大小的影响，可以采用公式C=c1f1+cyfy+cxyfxy-cxfx来表示PDC残余应力的大小。

［1］贾洪声，贾晓鹏，马红安，等.生长型金刚石复合片(PDC)的制备和残余应力研究［J］.超硬材料工程，2009，21(1):1-4.

［2］MUZAFFER Z，SADI K.Sintering of polycrystalline diamond cutting tools［J］.Materials and Design，2007(28):1055-1058.

［3］SCOTT D E.The history and impact of synthetic diamond cutters and diamond enhanced inserts on the oil and gas industry［C］//Proc 1st International Industrial Diamond Conference.Barcelona:［s.n.］，2005:1-21.

［4］PAGGETT J W，DRAKE E F，KRAWITZ A D.Residual stress and stress gradients in polycrystalline diamond［J］.Refatory Metals ＆ Hard Materials，2002，20(3):187-194.

［5］余伟炜，高炳军.ANSYS在机械与化工装备中的应用［M］.北京:中国水利水电出版社，2006:277-279.

［6］牛晓明，卢愕.有限元法与优化技术相结合的方法与应用［J］.光学精密工程，1995，3(6):107-108.

［7］王富耻，张朝晖.ANSYS10.0有限元分析理论与工程应用［M］.北京:电子工业出版社，2006:269-272.

［8］徐根，陈枫，徐国平，等.不同界面形态聚晶金刚石PDC热残余应力分析［J］.超硬材料工程，2007，19(4):10-15.

［9］徐国平，陈启武，尹志民，等.金刚石厚度对复合片(PDC)残余应力的影响［J］.高压物理学报，2009，23(2):24-30.