基于仿真优化的多种类型AGV数量配置优化方法
张远春 范秀敏,2 驹田邦久
1.上海交通大学,上海,200030 2.上海市网络化制造与企业信息化重点实验室,上海,200030 3.大金工业株式会社,大阪,日本,5300054
0 引言
AGV(automatic guided vehicle)在现代企业的车间物料搬运中发挥越来越重要的作用。AGV价格昂贵,且AGV的数量过多反而使其利用率降低,造成资源浪费。如何根据生产计划配置相应数量的AGV,使其满足产能需求一直是企业关注的问题。Egbelu[1]考虑AGV路径、装卸时间,提出了估算AGV数量的数学模型,但该模型没有考虑AGV的堵塞时间;王冰等[2]在Egbelu的基础上研究了不同的调度规则和不同交通管理下的AGV数量估算,但没有将调度规则与交通管理结合起来研究;Scrinivasan等[3]以KVehicles的方法分析AGV的调度规则为FCFS(先来先服务)时AGV的数量估计,该方法忽视了AGV数量多时交通堵塞的影响,估算误差大。
实际考虑AGV的数量配置时涉及的因素很多,如AGV的调度规则、AGV的容量、AGV的速度、交通拥堵情况等,很难建立精确的数学模型[4]。有学者将仿真模型和优化算法相结合,用于解决调度规则序列的优化问题[5]。鉴于此思想,本文先建立AGV的仿真模型,通过模型来表达AGV的路径、调度规则、交通管理等约束;然后利用此仿真模型,并结合遗传算法的智能搜索功能,得到AGV的最佳数量配置。
1 问题描述

图1 生产车间布局
图1所示为一生产车间布局,该生产车间由加工中心、配料区及成品库存区组成,物料在车间的流动是由n种AGV来完成的。每一种AGV负责一块区域,区域i对应的AGV数量(第i种AGV的数量)为Ni。如果某一区域的AGV的数量Ni过小,物料来不及运输,影响零部件的加工;反之,AGV的数量Ni过大,AGV利用率下降,也容易产生交通堵塞。因此AGV的数量配置优化问题描述为:给定工艺布局、AGV的路径、调度规则、AGV的速度等约束条件,确定每种AGV的最佳数量 Ni-best,使得输出产品数最大。同时,AGV的利用率不能过低。AGV数量配置优化的数学模型描述如下:

式中,Q为产品输出;f(*)表示产品输出与AGV的数量的关系;Ni,min、Ni,max分别为第i种AGV的最小数量和最大数量;Pij为第i种AGV中的第 j辆的利用率;Pi,min为第i种AGV的最小利用率;P(*)表示AGV必须满足的工艺约束;R(*)表示AGV必须满足的路径约束;D(*)表示AGV必须满足的调度规则约束。
式(1)(目标函数)表示产品输出最大,式(2)表示每种 AGV数量的边界;式(3)表示每种AGV的利用率不能低于边界值;式(4)~式(6)分别表示工艺约束、路径约束、调度规则约束。由这些约束条件难以建立数学模型,故本文通过仿真模型来表达这些约束条件。
2 仿真优化
2.1 仿真优化原理
仿真优化的基本原理是,利用仿真模型来替代传统优化模型中的目标函数和约束条件,由优化算法产生一组初始解,将该初始解输入到仿真模型,仿真一段时间后,得到这组解的性能指标,将这组解及其性能指标输入到优化算法中搜索迭代得到一组新解,这组新解比迭代前的解性能更优,再将新解导入到仿真模型,如此反复直到性能指标满足要求,输出最优解[5-6],如图2所示。
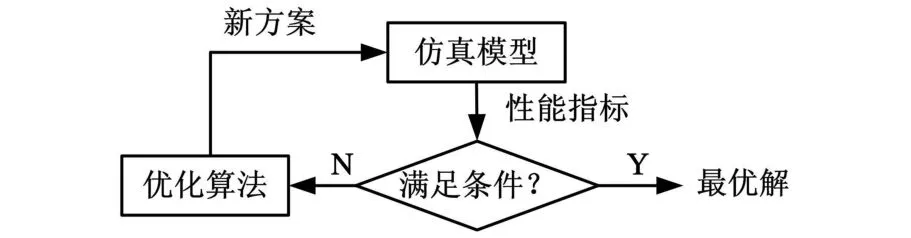
图2 仿真优化原理图
仿真优化不同于传统的优化,也不同于仿真实验,具体表现在如下几方面:
(1)传统的优化都是先建立解析模型,再利用优化方法来进行求解的。但是由于实际问题的复杂性和随机性,故很多问题是很难建立精确模型的。而仿真作为一种建模方法,能够把要素之间的逻辑关系通过建模语言表达出来,真实地反映系统的规律。
(2)仿真优化与仿真实验不同。仿真实验通过枚举方式对可能的组合进行逐一实验,搜索目标不明确,并且当组合数较多时,这种方法变得复杂、耗时长,甚至无法得到最优解。仿真优化将仿真与各种优化算法结合起来,发挥优化算法的搜索特长,在有限的时间内得到最优解。
根据仿真优化原理,本文提出的AGV数量配置优化方法(图3)由主控流程、遗传算法和仿真模型三部分组成。主控流程控制整个优化进程,包括初始种群生成、数据传递、种群信息显示;遗传算法产生新的AGV数量配置方案;仿真模型负责种群适应值计算。三部分相互协调完成AGV数量配置的优化。

图3 AGV数量配置优化方法
2.2 遗传算法
仿真优化下的遗传算法与传统优化下的遗传算法不同,主要表现在以下几方面:①目标函数值是由仿真获取的;②仿真优化的时间瓶颈不在算法的迭代过程而在仿真过程。因此在设计遗传算法时要相应地考虑这些特点。
2.2.1 编码设计
本文的目的是要确定每一种AGV的数量,使生产线产量达到最大化。因此可以直接以AGV的数量来进行编码,例如第i基因位上的值代表第i种AGV的数量Ni。考虑到种群中的每个个体的适应值不是通过函数而是通过仿真来获取的,因此在编码时增加基因位代表该个体的适应值即目标值(图4)。
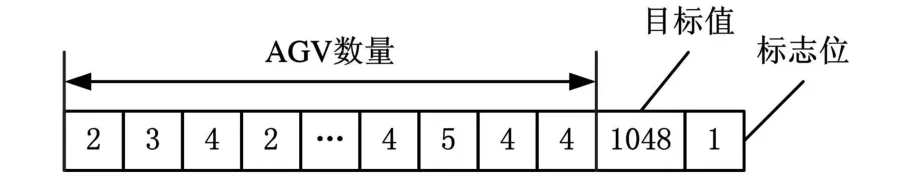
图4 基因编码
编码时还应考虑到仿真优化大部分时间消耗在仿真过程,减少这部分时间将提高优化速度。在遗传算法迭代过程中,子代与父代之间有相当一部分个体是相同的,在遗传算法后期收敛时,子代与父代的差异更小。因此可以考虑在每次迭代完成之后,将子代与父代个体进行比较,如果有相同个体,则它的适应值直接从父代获取不需要再仿真;相应地在编码上增加一标志位,如果该个体与父代个体相同,置标志位为1。仿真计算时如果发现这个基因位为1,就不启动仿真计算。甚至可以考虑将每次进化得到的父代存储为历代表,将子代与该历代表进行比较,优化进程会更快。
2.2.2 初始种群数生成
为了避免遗传算法过早收敛,采用随机的方式生成初始种群,具体步骤如下:
(2)对个体的每个基因位产生一个[Ni,min,Ni,max]内的随机数ri,将该随机数赋给基因位。
(3)将个体导入到仿真模型中,得到该个体的适应值,将该值赋给该个体的目标值基因位,同时标志位赋值为0,如图4所示。
(4)重复步骤(2)~(3)N次,产生一个包含N个个体的种群。
2.2.3 适应值函数
由于第1节的数学模型含有边界约束(式(3)),故可将该边界约束以惩罚函数的形式合并到目标函数:

2.2.4 选择操作
采用轮盘赌的选择方式从父代选取个体生成下一代。编码中包含了该个体的适应值,执行选择操作时,适应值直接从编码中提取。需要注意的是,选择操作一定要先于交叉和变异操作。一旦执行交叉或变异操作,编码中的适应值将是无效的。
2.2.5 交叉操作
交叉是将两个父代的部分基因进行替换、重组而产生新的个体,这里采用两点交叉(图5)。不同个体同一位置的基因表示同一种AGV的数量,基因的范围是相同的,因此通过交叉不会产生非法解。

图5 交叉算子
2.2.6 变异操作
变异算子能够提高算法的局部搜索能力,维持群体的多样性,防止过早收敛[7]。这里采用均匀变异。每次变异时,根据每一种AGV的数量[Ni,min,Ni,max],产生[Ni,min,Ni,max]之间的随机数(图6中的基因位)。这样可以避免非法解,同时又能保证搜索覆盖整个解空间。

图6 变异算子
2.2.7 迭代终止条件
本文采用的终止条件:遗传算法在迭代过程中,如果连续20代目标值没有变化,停止迭代。
2.2.8 控制参数选择
控制参数包括群体规模 N、交叉概率Pc、变异概率Pm。群体规模过小,容易收敛到局部最优解;规模过大,会造成计算量过大,群体规模一般根据实际在10~200之间选择。交叉概率Pc过大,群体中的优良个体破坏的可能性大,使搜索走向随机化;交叉概率Pc过小,进化速度变慢,甚至停滞。一般Pc取值范围为0.1~0.99。同样,当变异概率Pm很小时,易产生未成熟收敛,而增大Pm的值可以使解空间保持多样性,一般取为0.0001~0.1。
种群的规模选择20,由于搜索空间比较大,本文根据遗传算法进程选择不同的交叉概率和变异概率,在遗传算法的初期强交叉强变异(Pm=0.01,Pc=0.7),在遗传算法后期弱交叉弱变异(Pm=0.001,Pc=0.1)。
2.3 AGV仿真模型建立

图7 AGV的建模
整个仿真模型可以分成两部分,即加工部分和AGV物料运输部分(图7)。加工部分包括工位、输入输出缓冲区、配料区和成品仓库。AGV物料运输部分可进一步分为AGV控制层和AGV执行层。当加工区有物料运输需求时,就触发物料运输事件,AGV控制层检测到该事件后,就根据AGV调度策略选择一辆空闲的AGV并向其发送物料运输指令。AGV接受到该指令后,根据指令的相关信息执行该指令,在该过程中,AGV如果发生堵塞或碰撞,AGV控制层就会调用交通管理策略来协调AGV的运行。AGV任务完成之后,如果没有新任务就调用AGV停车策略,使AGV停在指定位置。在整个任务处理过程中,AGV状态表、物料运输事件表始终根据AGV状态及AGV对任务处理情况实时更新。
3 实例
3.1 装配线布局及其他相关数据
以日本大金工业株式会社空调装配车间为例,利用仿真优化方法对其车间的AGV的数量配置进行优化。该空调装配车间有3条装配线,每条装配线都能独立完成空调的装配,只是产品的型号不同。每条装配线需要3种物料,这3种物料位于不同的配料区,A1线的a种物料位于A_A1区域,如图8所示。这样3条装配线共9种物料,对应有9块配料区,物料从配料区到装配线对应由9种AGV来完成运送。图8所示为该装配车间的布局,图中实线表示的是AGV的路径,从图中可以看出,该车间AGV的路径重叠、交叉比较严重,不同种类、不同速度的AGV运行经常出现堵塞、需要避撞的情况。
9种AGV的数量范围均为[1,10];路径选择规则为最短路径规则;调度规则为先到先服务;交通协调规则为红绿灯协调法;最低利用率为60%;运送a种物料的AGV速度为500mm/s;运送b种物料的AGV速度为500mm/s;运送c种类物料的AGV速度为450mm/s;3条装配线的节拍因产品型号而异。
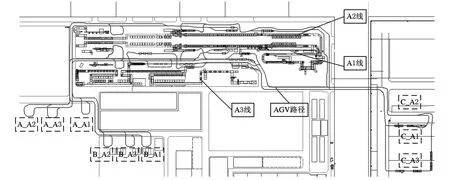
图8 AGV路径及装配线布局
3.2 仿真优化的实现
根据仿真优化的思想,本文提出的优化方法分成三大模块(图9):遗传算法模块、主控模块和仿真模块。主控模块控制整个优化进程,包括初始种群生成、数据传递、种群信息显示。优化模块利用MATLAB的遗传算法包,该算法包含大量与遗传算法操作相关的函数;同时 MAT LAB Engine提供数据接口,实现与其他模块的数据交互。仿真模块采用仿真软件QUEST,它自带的仿真语言SCL能够对复杂的逻辑关系进行建模,同时QUEST提供SOCKET数据通信接口,可以通过主控模块与优化模块进行数据交互。图10所示为建立的仿真模型。
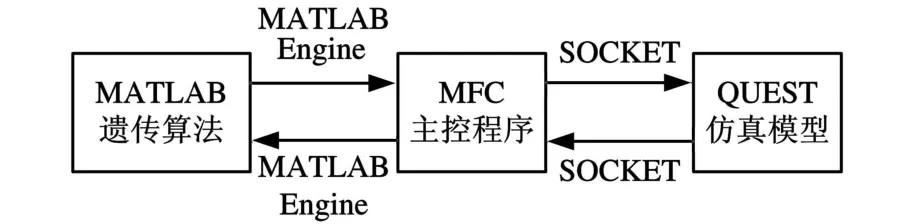
图9 仿真优化的实现
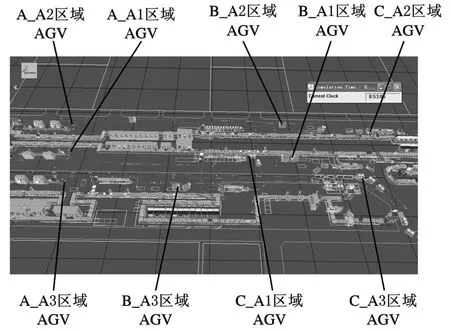
图10 AGV仿真模型
3.3 仿真优化结果
AGV数量配置优化进程如图11所示,遗传算法在第96代收敛,目标值为361。对应的9种AGV最佳数量配置为[3,3,5,2,3,4,2,3,5]。由此可见,利用仿真优化方法对AGV数量配置的优化的可行性。表1是仿真优化方法和其他估算方法的结果,从目标值可以看出仿真优化方法的结果更优。

图11 遗传算法进程
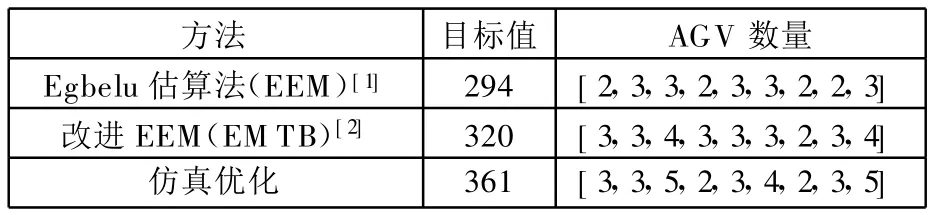
表1 结果比较
4 结语
本文以输出产品数最大化为目标,以AGV的数量配置为决策变量建立了问题的数学模型;针对该问题的复杂性,提出了仿真优化方法,讨论了该方法的实现问题;最后通过对日本大金工业株式会社空调装配车间AGV数量进行优化来验证方法的有效性及实用性。
[1]Egbelu P J.The Use of Nnon-simulation Approa-ches in Estimating Vehicle Requirements in an Automated Guided Vehicle Based T ransport System[J].Material Flow,1987,4:17-32.
[2]王冰,张惠侨.自动导向系统的规划设计[J].上海交通大学学报,2001,35(12):1793-1797.
[3]Srinivasan M M,Bozer Y A,Cho M.Trip-based Material HandlingSystems:Throughput Capacity Analysis[J].IIE Transactions,1994,26(1):70-89.
[4]Iris F A Vis.Survey of Research in the Design and Control of Automatic Guided Vehicle Systems[J].European Journal of Operation Research,2006,170(3):667-709.
[5]王国新,宁汝新,王爱民.基于仿真的生产调度优化技术研究[J].计算机集成制造系统,2007,13(7):1420-1427.
[6]王国新,宁汝新,王爱民,等.仿真优化在制造系统中的应用现状及发展趋势[J].系统仿真学报,2008,20(1):1-6.
[7]王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

