Kalman滤波器的硬件优化设计与仿真

白 雪， 王德明， 屠君君， 赵不贿

(1.江苏大学电气信息工程学院，江苏镇江212013；2.南京工业大学自动化与电气工程学院，江苏南京211816)

0 引 言

滤波是从带有干扰的信号中得到有用信号的准确估计值，Kalman滤波是一种时域内的滤波方法，它把状态空间的概念引入到随机估计理论中，估计过程中利用状态方程、观测方程和系统噪声及观测噪声的统计特性形成的一种滤波算法[1]。根据实时递推的思想，Kalman滤波过程是一个不断“预测-修正”的过程[2-4]，求解中无需存储大量数据，一旦观测到新的数据就可以计算出新的滤波值，因此方便硬件实现，在实际工程中得到了广泛应用。因此对Kalman滤波算法的实现是很多工程应用中首要解决的问题。

在一些实时性要求较高的场所，传统的器件由于其固有的结构特点，较难完成如并行计算等对性能要求较高的应用。而FPGA作为一种典型的以资源换取性能的器件，随着工艺水平的不断提高，其规模越来越大，性价比也越来越高。其内部的大容量本地存储器、高速I/O等极大地提高了FPGA在数字信号处理领域中的应用潜力，特别适合实时性要求较高或计算量很大的场合[5]。如Vanderlei Bonato在全自动机器人上成功利用FPGA实现了浮点扩展Kalman滤波器[6]，实时地完成了复杂的运算；喻金华基于FPGA平台设计和实现了图像滤波的流水线结构[7]。随着微电子技术和EDA技术的发展，FPGA的集成度和速度可以最大限度地满足系统的灵活性和实时性。

近年来，很多学者基于FPGA平台进行了Kalman滤波器的设计和应用[8-11]。周倩将车辆组合导航中的Kalman滤波器在FPGA上实现[12]。但是设计重点强调运算速度和实时性，利用FPGA的并行运算特点，以面积换速度，在提高系统实时性的同时，消耗了大量硬件资源，不利于系统的升级和灵活实现。冯安详基于FPGA设计的目标运动预测Kalman滤波器保证实时性的同时考虑了资源占用问题[13]，但其采用单精度运算，在精度要求很高的环境下稍显不足。

本设计针对Kalman滤波器的硬件构成结构进行了优化，采用双精度浮点运算，利用IP核和分时复用技术，在提高运算精度的同时提高了系统的实时性，又尽可能地降低硬件资源消耗，使设计实现更灵活方便。

1 Kalman滤波算法过程描述

选取文献[14]中的GPS系统方程和观测方程，借鉴其分散滤波算法对无耦合的X、Y方向分别建立递推的Kalman滤波方程，以X轴向为例，状态变量选为=[ ]，系统方程为

系统噪声矢量为

式中：——加速度相关时间常数， —— (0,2)的高斯白噪声。系统观测方程为，观测矩阵为=[1 0 0 1]，观测噪声矢量为Vx=[ ]， 为(0,)的高斯白噪声。根据上述系统方程、观测方程和Kalman滤波算法，得到X轴向上Kalman滤波方程

以上公式描述的Kalman滤波计算过程如图1所示。

2 基于IP核和分时复用技术的滤波器设计

2.1 采用分时复用技术的硬件总体设计

Kalman滤波算法在此实现GPS数据的滤波，并输出滤波后结果，减小误差，提高定位精度。该滤波系统的外部接口信号如表1所示。

根据自顶向下的设计思路，构建顶层模块、存储模块以及Kalman变量运算模块。其中Kalman运算模块是系统设计核心，实现Kalman各变量的递推计算，由系统一步预测估计、系统状态估计、系统滤波增益、系统一步预测估计误差方差和系统滤波误差方差5部分构成。

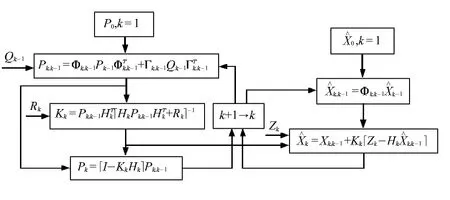
图1 Kalman滤波计算框架

表1 Kalman滤波模块的接口信号

为提高资源利用率，在顶层模块设计中，将Kalman各个运算模块进行分时复用，系统结构如图2所示。分时复用过程中运算数据切换时，将观测量和预测值存入First-In-First-Out(FIFO)中，利用FIFO先进先出的特点确保每次观测量和预测量的匹配。

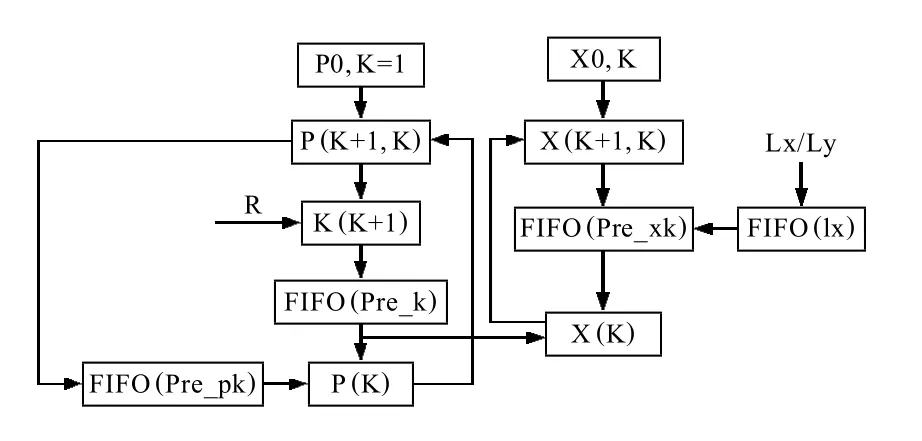
图2 Kalman滤波器的分时复用结构

系统初始化时，由GPS提取出来的数据信息lx不写入FIFO(lx)中，而是将作为X0的初始值。分别用pre_pk，pre_k和pre_xk表示预测量P、K和XK，将预测得到的结果分别存入各自的FIFO中。首先存入的是Y坐标预测的值，接着是X坐标预测的值。然后启动整个系统的工作，等观测值的输入之后，首先从各自的FIFO中读取出预测值进行PK和XK值的计算，再根据这两个值预测P、K和XK的值，依次类推。Y和X的预测值依次存入FIFO中，与输入的观测值一一对应。

2.2 基于IP核和分时复用的运算模块结构设计

为确保数据处理精度，系统设计中采用双精度浮点运算。为提高实现效率，在滤波器各个模块中调用了浮点加减、浮点乘除的IP核[15]。

下面对主要的IP核加/减法器IP和乘法器IP进行了功能测试。浮点的加法是先将一个数的尾数右移或者左移几位，当两个数的指数相同时将尾数相加得到。通过operation端口来实现加法或者减法的切换。乘法器的IP核有两种类型：用专用乘法器实现和用 Slice搭建乘法器。由于一个浮点乘法器的实现需要16个专用乘法器，整个设计中共使用到6个浮点乘法器，考虑到资源和模块的通用性，设计中选择通过slice实现乘法器的搭建。图3是仿真测试结果，结果表明该乘法器IP正确的实现了乘法运算功能，其中输出滞后输入9个时钟周期。

图3 乘法器IP核测试

由于浮点IP核占用资源较多，所以在满足实时性的前提下，进行了各个模块基于IP核的分时复用结构。以系统一步预测估计误差方差(pre_p)模块的结构设计为例。由滤波方程得

矩阵各元素如下

根据推算，完成系统一步预测估计误差方差模块需要做26次加减法运算和16次乘法运算。而通过时分复用，模块结构中只需用到一个乘法IP核和一个加减IP核，设计该模块的时序如图4所示，得到图5的模块结构。可见，分时复用优化结构大大提高了资源的利用率，降低了硬件实现时对资源的要求。完成预测估计方差的运算共需要69个时钟周期，实时性可以得到保障。

对于系统滤波增益模块，由滤波方程可以得到

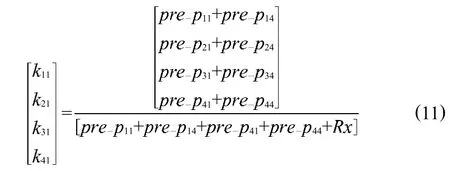
该模块通过时分复用，用到一个加法器和一个除法器IP核，结构如图6所示。

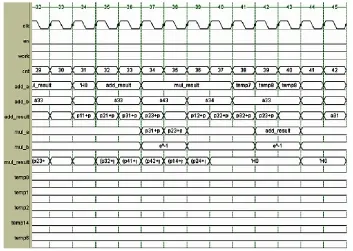
图4 系统一步预测估计误差方差模块时序设计

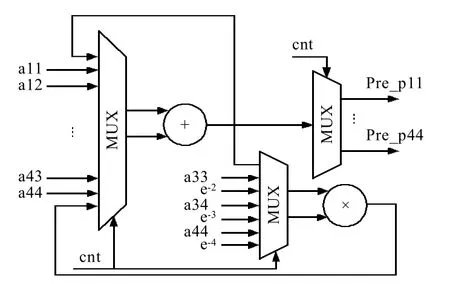
图5 系统一步预测估计误差方差模块结构

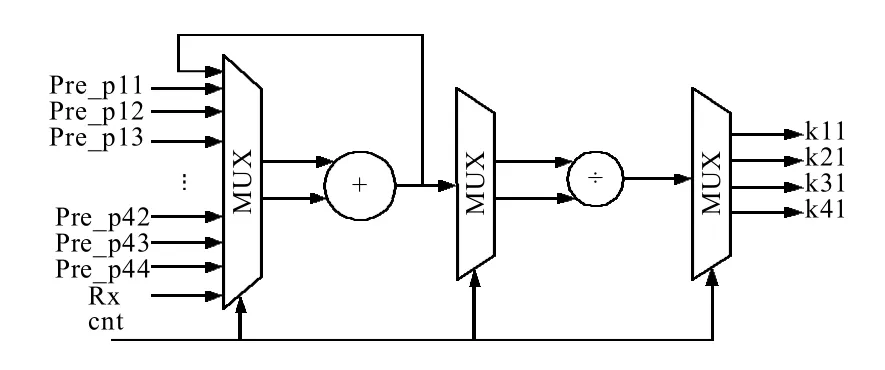
图6 系统滤波增益(pre_k)模块结构

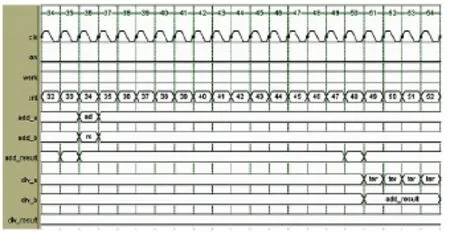
图7 系统滤波增益(pre_k)模块时序

整个模块的时序如图7所示。当检测到en为1时，即外部输入P预测值已经运算完毕，则开始工作。工作状态用work信号表示，若work为1时表示模块处于工作状态，否则为闲置状态。在复用 IP核的过程中通过用中间变量暂存需要的结果。add_a、add_b、add_result、div_a、div_b 以及 div_result分别是加法器和除法器的输入输出端口。计算滤波的增益模块共需要109个时钟周期。

通过对其他运算模块进行分时复用的时序分析和结构设计，完成整个Kalman变量的运算模块需要234个时钟周期，运算满足系统的实时性要求。

3 实验数据的获取及系统仿真

GPS定位原始数据为江苏大学电气学院4楼实验室的静态定位数据，所用接收机为星网宇达公司的 GPS OEM板GPS-1000，RS232串口通信，数据格式为NMEA0183。实验获取的原始经纬度定位数据经高斯投影后转换为平面坐标，以此作为滤波系统的输入数据，即滤波对象。

基于Xilinx的xc5vtx240硬件平台，在Modelsim环境下对所设计的Kalman滤波系统及GPS定位数据进行了半物理仿真，结果如图8所示。由于在系统设计中，对于x,y方向采取了整个模块的分时复用，则图中xk有效值第一个对应的是y值，第二个对应的是x值，以此类推。

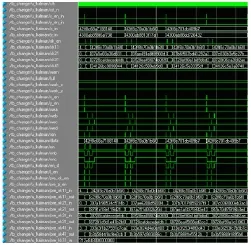
图8 Kalman滤波模块的Modelsim仿真波形

由于图8中数据为双精度浮点表示，不便于观察，为了更直观分析滤波效果，将滤波后的 Modelsim仿真数据导入到Matlab环境，与滤波前的原始数据进行对比，如图9所示。两种仿真结果表明：设计的浮点Kalman滤波器满足系统实时性要求，若时钟频率为50MHz，则完成一个周期运算只要4.68 s，而同样的算法用DSP或单片机通过软件实现一个运算周期则需要几百 s甚至更长时间；设计的Kalman滤波器可以减小定位误差，提高定位精度，达到系统设计的目的。

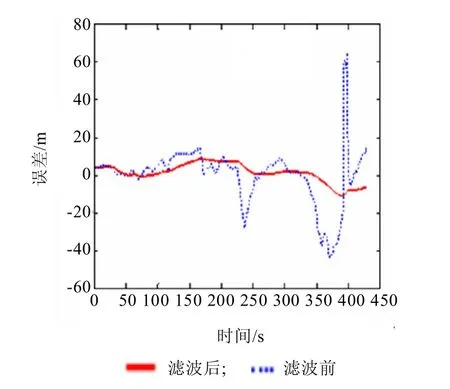
图9 Kalman滤波前后GPS定位误差比较

本设计使用双精度浮点运算，能够满足在数据精度方面要求高的场合。在Xilinx的xc5vtx240上编译综合后，显示其资源占用情况如图10所示。若应用在精度要求相对较低的环境中，将数据位宽降低，资源消耗将会大量减少。

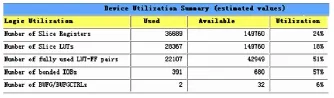
图10 双精度浮点的资源消耗

Modelsim仿真结果表明，该滤波器的设计可以满足系统实时性要求。以提高GPS的精度为背景，其Matlab仿真结果表明，该滤波器可以有效降低定位误差，提高了精度，具有实际应用价值。

4 结束语

基于FPGA平台设计的浮点Kalman滤波器，根据算法优化了底层硬件结构，充分利用了IP核、模块的分时复用技术，以速度换面积，提高了资源利用率，且结构利于硬件实现。更重要的是，FPGA具有灵活的可移植特性和优良的抗干扰能力，因此所设计的滤波器易于修改、测试和算法升级。在保证精度的前提下很好地解决实时性问题和资源占用问题，具有更广泛应用性和实际工程意义，其设计思想和方法具有通用性。

[1]SimonD.Kalmanfilteringwithstateconstraints:asurveyoflinear and nonlinear algorithms[J].Control Theory&Applications,2010,4(8):1303-1318.

[2]Welch G,Bishop G.An introduction to the Kalman Filter[Z].University of North Carolina,2004.

[3]David M Bevly,Parkinson Bradford.Cascaded Kalman filters for accurate estimation of multiple biases,dead-reckoning navigation,and full state feedback control of ground vehicles[J].IEEE Transactions on Control Systems Technology,2007,15(2):199-208.

[4]Fang Jiancheng,Gong Xiaolin.Predictive iterated Kalman filter for INS/GPS integration and its application to SAR motion compensation[J].IEEE Transactions on Instrumentation and Measurement,2010,59(4):909-915.

[5]田耘,徐文波,胡彬,等.Xilinx ISE Design Suite 10.x FPGA开发指南——逻辑设计篇[M].北京:人民邮电出版社,2008.

[6]Bonato V,Marques E,Constantinides G A.A floating-point extended kalman filter implementation for autonomous mobile robots[C].International Conference on Field Programmable Logic and Applications,2007:576-579.

[7]喻金华,肖铁军.基于FPGA的图像滤波的流水线结构设计和实现[J].计算机工程与设计,2009,30(18):4192-4194.

[8]Bonato V,Peron R,Wolf D F,et al.An FPGA implementation for a Kalman filter with application to mobile robotics[C].International Symposium on Industrial Embedded Systems,2007:148-155.

[9]Idkhajine L,Monmasson E.Optimized FPGA-based extended Kalman filter application to an AC drive sensorless speed controller[C].International Symposium on Power Electronics Electrical Drives Automation and Motion,2010:1012-1017.

[10]Idkhajine L,Monmasson E,Maalouf A.Fully FPGA-based sensorless control for AC drive using an extended Kalman filter[C].35th Annual Conference of IEEE Industrial Electronics,2009:2925-2930.

[11]Yang Liu,Bouganis C S,Cheung P Y K.Efficient mapping of a Kalman filter into an FPGA using Taylor expansion[C].International Conference on Field Programmable Logic and Applications,2007:345-350.

[12]周倩.车辆组合导航中卡尔曼滤波器的设计及FPGA实现[D].北京:北京交通大学,2009.

[13]冯安详,肖阳辉,王玉良,等.基于FPGA的目标运动预测实时kalman滤波器设计[J].电子技术应用,2008(7):49-51.

[14]李康吉,刘国海.一种提高GPS定位精度的组合定位方法[J].东南大学学报,2004,34(11):88-91.

[15]Xilinx Corporation.Spartan-3E Starter Kit User Guide[Z].2006.