泵车疲劳损伤计算中的奇异值剔除方法

吴运新，胡 凡，滑广军

(中南大学机电工程学院湖南长沙410083)

0 引言

奇异值剔除是数据处理中一个重要环节.奇异值［1］又称为野值，是指不是被测对象本身正常信号的记录，而是由于传感器、变化电路以及外界电磁干扰等造成的异常跳点，也即是测量设备在传输过程中出现异常导致的不正确点.

混凝土泵车前期的应力测试及有限元分析表明，泵车臂架的应力幅值在臂架结构材料强度0.5倍以下，属于高周疲劳问题.因此在计算泵车臂架结构的疲劳损伤时采用Palmgren-Miner(潘格伦- 迈纳)线性累积损伤理论［2］，即：

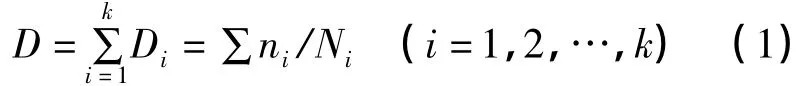
式中：ni为应力Si对应的频次;Ni为S-N曲线应力Si对应下的寿命.

利用潘格伦-迈纳模型计算结构疲劳累积损伤，需要知道结构载荷谱(即应力Si对应下的频次ni)和结构S-N曲线.结构S-N曲线是通过材料S-N曲线通过修正得到的，结构载荷谱是通过测试的应变信号经过雨流计数和等效应力转换得到的.

因此，在进行雨流计数［3］时，如果存在奇异值，将会使疲劳损伤计算产生误差，对后期疲劳分析产生影响.所以，在进行雨流计数前，必须对采样所得的应变信号进行奇异值的剔除.

1 奇异值剔除方法

目前在工程应用的数据预处理中奇异值的剔除一般采取两种方法.第一种方法是利用测量数据的估计值和测量值的差值(即残差)对奇异值进行判别和剔除，如kalman滤波法等.另外一种方法是对测量值进行统计检验，通过统计规律来检测是否含有奇异值.如罗曼诺夫斯基(Romanovsky)准则［4］、狄克松(Dixon)准则、肖维勒(Chauvenet)准则［5］、格拉布斯准则［6］、莱特准则等.

第一种方法精度较高，检测效果较为明显，但在工程实际应用中，尤其是数据的在线处理上，缺乏精确数学模型的支持.因此该方法不太适合用于工程机械的测试数据处理中.而第二种方法中除了莱特准则外，其他算法都需要预判测量值统计特性，在噪声统计特性事先无法得知的情况下，实用性受到限制.

莱特准则又称为3σ准则［7］，3σ准则的判定值为常系数，而泵车臂架应变信号随着姿态和泵送情况的改变而发生较大的变化，其变化规律不尽相同，即使在同一工况下，其变化规律也不一定一致，所以使用3σ准则进行奇异值的判断有一定的局限性.另外，3σ准则通常在对同一段信号多次测量的基础上进行奇异值剔除的把握性较大，而泵车应变信号是随着泵车工作时间不断采集的，是一次性测量，所以使用3σ准则势必会对计算结果造成误差.

针对3σ准则在处理泵车应变信号上的缺点，笔者提出了一种奇异值剔除方法，即利用应变信号的变化率来剔除奇异值.

2 变化率法

混凝土泵车臂架主要受其自重导致的静态力和泵送液压冲击引起臂架振动导致的动态力，其中液压冲击力通过车身作用到臂架上，其受力示意图如图1所示.姿态的变化导致臂架整体结构改变，所以泵车臂架的应力应变水平主要由泵车的姿态和泵送引起的振动所决定.

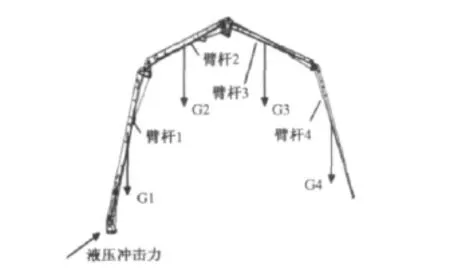
图1 泵车臂架受力示意图Fig.1 The force diagram of truck mounted concrete pump boom

泵车在一种工况下其姿态是不发生改变的，这时仅受泵送时的振动冲击对臂架应力的影响.对某公司37 m泵车臂架结构各种典型姿态的有限元模态分析表明，泵车臂架结构的第一阶固有频率在0.3～0.47 Hz之间，而泵送频率为20～28次/min，泵送频率比较接近其一阶固有频率，因此泵车的泵送对臂架应力水平的影响比较大.因此，泵车臂架应变信号具有以下特点：应变信号的整体水平会随着泵车姿态变化而发生变化，姿态不变时每泵送一次应变信号会有一次波动，而在两次泵送期间臂架应变信号比较平稳，不会出现较大的波动.另外，当泵车在启动或停止情况即应变信号有明显的上升趋势或下降趋势时，由于其时间较短且应力水平较低，即使应变信号存在奇异值，对泵车臂架疲劳损伤的影响也很小.所以笔者讨论的对象是泵车正常工作时的应变信号.

根据上述应变信号的特点，两次泵送期间内应变信号较平稳，如果该段信号内某信号点出现较大波动甚至突变，则视其为奇异值点.因此可以利用应变信号变化率作为判断奇异值的依据，计算某信号点前一段时间内各应变信号点的数据变化率，找出变化率的最大值.选择该最大值作为判断该信号点是否为奇异值的范围，如果该信号点的变化率在这个范围内就为正常的应变信号，若超出便判定为奇异值，予以剔除.根据泵送频率N次/min和应变信号采样频率50 Hz，取两次泵送之间(泵送周期内)的数据段为剔除奇异值数据段长度，除去泵送时应变信号发生突变的首尾点，即待处理的数据段内有60/N×50-2个信号点.

首先，对前q(q≥10)个信号点进行最小二乘多项式拟合［8］，即根据前 q 个信号点(ti，εi)(i=1，2，3，…，q)构造 n 次多项式：

式中：φn(t)=tn，t为采集时刻.计算 a0，a1，…an使得最小，从而求得φ(t).

前q个信号点用拟合所得的值代替原始数据值，以上完成算法的初始化过程.

然后，计算待处理数据段内信号点变化率：

判断序号为k的信号点时，定义剔值带ScopeA(k)，ScopeB(k)：

这两个剔值带的物理意义是：计算k信号点前q个信号点应变数据变化率的最大值，将此最大值作为k信号点数据变化率的最大范围，通过判断k信号点数据变化率是否超过这两个剔值带来判断是否出现奇异值，并根据其奇异值偏离正常范围的程度来分别剔除奇异值.其中m值随应变信号的波动情况而变化.

如果应变数据εk的变化率的绝对值大于ScopeB(k)，主要采用k信号点前的数据段进行切比雪夫拟合［9］，根据拟合的曲线得出该信号点应变数据的修正值.

现需要对时间间隔［t0，t0+(k-1)T］(其中t0为泵送起始时刻，T为采样周期)内的一批信号点(ti，εi)(其中 ti为采样时刻，εi为应变数据)，将变量t变换成x∈［-1，1］

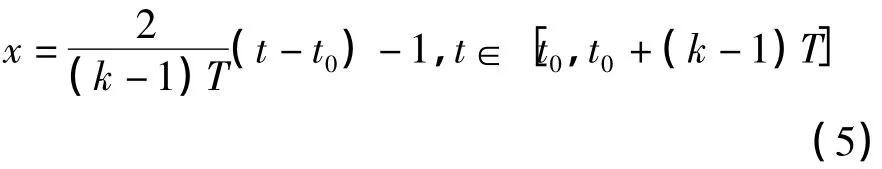
然后对信号点(xi，εi)(i=1，2，…，k-1)，计算其n阶切比雪夫多项式：

的系数 c0，c1，…cn使得

最小.在切比雪夫多项式中根据如下递推公式确定 φj(x)：

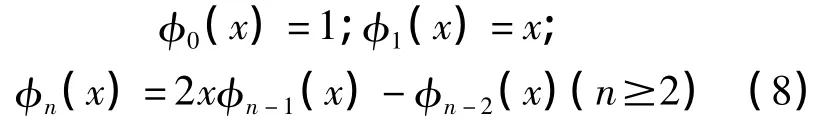
将x=kT代入公式(6)，就可以得到奇异值点应变数据的修正值.

如果应变数据εk变化率的绝对值大于ScopeA(k)而小于ScopeB(k)，主要采用k信号点应变数据加上该信号点应变数据变化梯度的一半来修正奇异值点应变数据，即以εk+(εk-εk-1)/2代替.其目的是允许应变信号出现较小的波动，这是因为混凝土在输送管中运动时也会对泵车臂架应力水平产生较小范围的影响.

3 仿真分析

3.1 与3σ准则剔除效果的比较

为了验证变化率法在剔除泵车臂架应变信号中奇异值的可行性，取泵车某次试验没有较大突出值的实测42 min应变信号(其中泵送频率N=20)，即可以认为该段信号没有奇异值，计算的载荷谱和疲劳损伤值为真值.在该段信号内人为给定一定数量孤立的奇异值，然后通过Matlab分别仿真计算含有奇异值模拟应变信号、3σ准则剔除奇异值后应变信号、变化率法剔除奇异值后应变信号的载荷谱和损伤值，与原始应变信号的载荷谱和疲劳损伤值(真值)相比较.

泵车原始(真值)应变信号，含有奇异值的模拟应变信号，3σ准则剔除奇异值后的应变信号、变化率法剔除奇异值后应变信号，见图2.

通过雨流计数和损伤计算后的载荷谱，见图3.疲劳损伤值见表1.

从应变信号图上可以直观的看出，利用变化率法剔除孤立奇异值后奇异值点明显减少，而3σ准则剔除孤立奇异值后奇异值点仍然还大量存在.从二维载荷谱可以看出含有孤立奇异值的二维载荷谱在应力幅值40～70 MPa之间的次数都大于原始信号所对应的应力幅值的次数;利用变化率法剔除奇异值后的二维载荷谱与原始信号的二维载荷谱只在应力幅值40与50 MPa的次数不同，且次数仅相差1次;而利用3σ准则的二维载荷谱与原始应变信号的二维载荷谱在应力幅值多处的次数都不同，且次数相差较大.二维载荷谱的差异直接导致疲劳损伤值的不同.从表1中各疲劳损伤值，可以看出奇异值会造成疲劳损伤值的增大，利用变化率法进行孤立奇异值剔除后可以减小其与损伤真值的差距，并且减小的幅度比3σ准则更大，是较为合适的泵车臂架应变信号剔除孤立奇异值方法.

表1 应变信号对应的疲劳损伤值Tab.1 Fatigue damage of the strain signal

从载荷谱和疲劳损伤值还可以看出，通过变化率法剔除奇异值后得出的疲劳损伤值和真值还是有误差，这里的误差主要由以下几个方面造成：一是原始信号中也含有少量的奇异值;二是信号中奇异值不能完全剔除干净;三是奇异值点的修正值不能完全符合原始值，拟合曲线尽管误差很小，但始终存在误差.

3.2 对连续型奇异值的剔除效果

为了比较出现连续奇异值类型时变化率法的剔除效果，在原始应变信号中分别加入不同连续类型的奇异值.利用变化率法进行奇异值剔除后的效果见表2.

表2 连续型奇异值的剔除效果Tab.2 Removing effect of continuous singular value

由表2可以看出，随着奇异值连续个数的增加，疲劳损伤值的大小也在变大，与原始真值的差值也在变大，这与4点法雨流计数的计数原理是一致的.利用变化率法剔除孤立、连续2个与连续3个奇异值效果较好，而在连续4个以及连续5个奇异值剔除方面效果会变差，这是由于为了防止连续采用过多的估计值，容易偏离原信号的真实性，第4个数据使用当前的采样值所导致.连续4个奇异值数据经过变化率法剔除后，变为仍然含有孤立型奇异值的数据.而对于更多连续个数的奇异值，由于在第4个数据(为奇异值)的变化率很大，导致其后奇异值的判定容易出现误判.当然，究竟在连续采用几个估计值后，原信号会失真，这需要针对具体的情况而定.因此，变化率法在剔除应变信号中连续个数不多的奇异值时效果会较好，而在剔除连续个数较多的奇异值时效果会变差.

4 结论

结合泵车臂架应变信号的特点，利用应变信号变化率作为判断奇异值的依据，相比3σ准则能够更为有效的剔除应变信号中奇异值.变化率法可靠性高，实用性强，有效地克服了传统3σ准则的缺点，并且可以实时剔除奇异值.随着泵车的老化，混凝土在输送管内运动对泵车臂架应力水平的影响越来越大，两次泵送期间的应变信号波动相应也会增加，可以通过应变信号的变化情况改变剔值带的范围来修正变化率法，从而保证泵车任何工况和工作寿命内其剔除奇异值的可靠性.

该方法不仅适用于泵车臂架应变信号，对其他领域的信号，也不失为一种有效的剔除奇异值方法.

［1］赵圣占，高成文.遥测数据处理的野值剔除方法研究［J］.强度与环境，2005，32(1)：59-63.

［2］姚卫星.结构疲劳寿命分析［M］.北京：国防工业出版社，2004：76-80.

［3］董乐义，罗俊，程礼.雨流计数法及其在程序中的具体实现［J］. 计算机技术与应用，2004，24(3)：38-40.

［4］王正明，易东云.测量数据建模与参数估计［M］.长沙：国防科技大学出版社，l996.

［5］张文博，李凯，朱尤攀，等.光电稳定跟踪平台中微机电陀螺滤波方法研究［J］.红外技术，2006，28(5)：249-252.

［6］沈一鹰，冉启文，刘永坦.改进的格拉布斯准则在信号检测门限估值中的应用［J］.哈尔滨工业大学学报，l999，31(3)：11l-113.

［7］何世彪，杨士中.3σ准则在小波消噪中的应用［J］.重庆大学学报，2002，25(12)：58-60.

［8］韩旭里，万中.数值分析与实验［M］.1版.北京：科学出版社，2006：79-84.

［9］邓倩妮，陈笠.基于复杂曲线表示的切比雪夫多项式拟合并行算法［J］.上海交通大学学报，2003，37(6)：906-909.