钢筋网对道路混凝土振动能量的阻隔研究

张艳聪，王大鹏，田 波，侯子义

(1.河北工业大学土木工程学院，天津300401;2.交通运输部公路科学研究所，北京100088)

0 引言

在工程施工中，利用机械密实混凝土的工艺方法很多，如振动、碾压、脱水、注浆等，其中以振动密实的方法应用最为广泛.尤其是在道路混凝土摊铺中，普遍采用振捣棒组振动密实混凝土.与普通混凝土相比，钢筋混凝土振动密实的区别在于钢筋网的存在会对摊铺机具振捣棒组的插入深度产生较大影响，深度太深则容易破坏钢筋形态，深度太浅混凝土则不易振实.钢筋网下的混凝土是否密实，钢筋网对振动能量的阻隔是钢筋混凝土振动密实环节必须注意的问题.

西南交通大学的张祖武［1］应用应力波在介质界面能量分配与反射和透射系数之间的相关性，得出了地震波在不同介质中滞留能量的耗散比与介质波阻抗比和上层介质能量衰减比之间的关系.水利部淮委水利科学研究院的秦厚慈［2］通过对浇筑过程中的零坍落度混凝土的振动加速度和时程曲线的实地测量，分析并论述了零坍落度混凝土的振动衰减规律、混凝土振捣密实所需要的持续时间等问题.笔者主要从振动加速度、分层密度入手，通过试验研究振动能量在混凝土中的传播规律，以及钢筋网对振动能量的阻隔作用，并给出相应的补偿措施.

1 振动能量在混凝土中的传播

道路混凝土的振动密实是通过摊铺机具的振捣棒组将机械能或电能转换为振动能，进而将混凝土液化，使其均匀的布满整幅路面，最终达到密实的效果.对于回转振动器来说，振动非常接近于谐振运动，如图1所示.图(a)为振捣棒体中的偏心块围绕回转轴转动，产生正弦振动波，如图(b)所示.这样的正弦波振动可以用振动频率、振幅等参数来描述［3-4］.

图1 回转振动器振动波示意Fig.1 Wave of whirl vibration

振动周期T为偏心块围绕回转轴转动一周所需的时间，s;振动频率f常用转速来表示，用式(1)计算.

振幅A0为运动y=Asint中位移的最大值，m;

振动速度v由式(2)计算

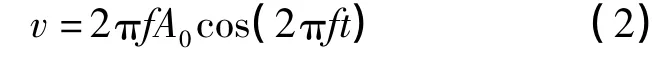
式中：f为振动频率，Hz;A0为振幅，mm;t为振动时间，s.

振动加速度a由式(3)计算：

最大加速度a0：振动加速度的最大值，m/s2，由式(4)计算，式中各参数含义同前.

振动最大动能k0，由式(5)计算.

式中：m为偏心块质量，kg;A为振动的平均振幅，mm.

研究表明［5-7］：不论是振动频率还是振幅都不足以单独决定振动效率.振动加速度、每周期的最大加速度a0，常用以衡量振动强度.下文中也将以a0评定振动能量在混凝土中(钢筋网上、下)的传播规律.

2 钢筋网对振动能量的阻隔作用

2.1 振动能量在混凝土中的传播规律

2.1.1 振动能量的测定

为测定钢筋网对振动能量是否存在阻隔，试验设计两组试件，如图2所示，试件体积参数为80 cm×80 cm×30 cm.图2(a)试件中部约15 cm处设置钢筋网，钢筋采用φ14螺纹钢筋，钢筋网规格为16 cm×16 cm;图2(b)为对照组，试件不设钢筋网.然后使用高频振捣棒(如图2中黑色部分)产生振动波，在试件内部布置加速度传感器，用DScope音频信号分析系统(如图3所示)测定同一时刻(振动施加约60 s［8］时)混凝土中水平、竖直两个方向多个测点的振动加速度.通过3组平行试验，比较设置钢筋网前后振动能量的变化规律.由于高频振动波波动较大，本研究所指的加速度取收集到的振动加速度的幅值.

图4所示为振动加速度传感器在混凝土试件中的布置示意，传感器沿水平、竖直两个方向布置，1，2，3 为测点位置.

图2 对照试验示意图Fig.2 Parallel experiment

竖直方向上，测点沿振捣棒方向布置，加速度传感器每隔5 cm布置一个，水平方向上每隔20 cm布置一个，1#测点紧临振捣棒体.振捣棒的插入位置如图4中黑色部分所示，棒体下端深入到试件中部，但不能与钢筋接触.振捣棒采用高频插入式振捣棒，振动参数如表1所示.

表1 插入式振捣棒的振动参数Tab.1 Vibration parameter

2.1.2 能量传播规律的试验结果及分析

未设置钢筋网的试件，水平、竖直两条测线上各测点的振动加速度如表2所示.由表中数据可知：两条测线上，振动加速度幅值均随距棒体(振源)距离的增加而减小.

水平测线上振动加速度幅值衰减显著，振动持续时间约50 s时，1#点位的加速度幅值为2 348.4 m/s2，而2，3 点幅值则由1 740.1 m/s2减少至722.6 m/s2，二者较1#点位分别了降低了25.9%，69.2%.竖直测线上，振动加速度幅值由1#点位的2 345.0 m/s2减少到2#点位的1 438.5 m/s2，再减少到 3#点位的 527.4 m/s2，2#，3#点加速度幅值相对1#点分别降低了38.7%，77.5%.

表2 各测点加速度幅值Tab.2 Vibration acceleration amplitude

设置钢筋网后，各测点的加速度幅值如表2所示.水平侧线上，1#点位的加速度幅值为2 350.5 m/s2，而2#，3#两点的加速度幅值较1#点分别降低了52.0%和80.9%.而竖直测线上，2#、3#两点加速度幅值相对1#点则分别衰减了62.6%，96.2%.

设置钢筋网前后，两条测线上振动加速度幅值的变化情况如图5所示.水平测线上，设置钢筋网的混凝土振动加速度从1点到3点衰减了1 625.8 m/s2，相比无钢筋网的1 900.8 m/s2降低了275 m/s2.即：水平方向上，振动能量经过单层钢筋网的阻隔，加速度损失了275 m/s2，约为振源处加速度的11.8%.而对于竖直方向上，这一损失则达440.7 m/s2，约为振源处的18.8%.因此，钢筋网对振动能量存在较明显的阻隔作用.

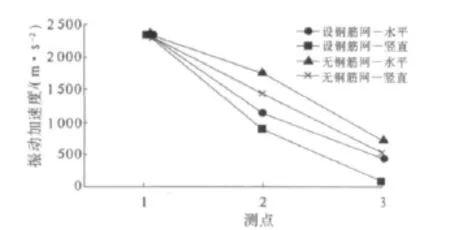
图5 各测点振动加速度的变化Fig.5 Changes in vibration acceleration

对于设置钢筋网的试件，试验结果还表明：当振捣棒插入深度至图4中2#点位时，竖直方向上3#点位的振动加速度仅为576.3 m/s2，远小于表2中2#点的振动加速度;振捣棒水平移动至图4中2#点位时，3#点位的振动加速度为864.4 m/s2，这一结果也远小于水平方向上表2中2#点的加速度.同时，当被振混凝土的一侧边界是已振实的混凝土，而另一侧边界为新拌混凝土时，振实混凝土附近的测点加速度小于新拌侧的加速度.

因此，振捣棒周边的介质及介质的状态影响着混凝土粒子振动加速度的分布，对振动能量在混凝土中的传播有一定影响.硬化混凝土或模板对与其接触的新拌混凝土粒子产生较强的约束，粒子不易运动，振动能量在该界面附近“失效”［9］，与新拌混凝土一侧的粒子相比的位移不同，振动加速度也不同.此外，底面混凝土的凝结状态对其上部浇筑层混凝土的振动加速度也有较大影响，底面混凝土已经终凝(或初凝)，其浇筑层混凝土振动加速度小于底面混凝土尚未终凝(或初凝)的加速度.这也是因为底面混凝土终凝以后已经变得刚硬，对新浇筑混凝土粒子的移位具有强约束作用.

2.2 振动能量的衰减

由2.1可知，无钢筋网的混凝土中，振动加速度沿振捣棒体的中心向周围逐渐减弱.设置钢筋之后，由于钢筋网的阻隔，振动加速度进一步衰减.为了定量的描述钢筋网对振动能量在混凝土中传播的阻隔引入振动能量衰减系数概念.

2.2.1 振动能量衰减系数

以测线上距离振捣棒棒体最近测点的加速度幅值作为基准值1，求出该测线上其余测点加速度幅值的相对值，然后除以相应的距离(测点距基准点)，即得到该测线上所有测点的振动能量衰减系数β，β可以有效表示振动能量在所测传播方向上单位长度的损失百分比.由振动能量衰减系数的概念可知：基准点的振动能量衰减系数为1 cm-1，测线上其余各点的能量衰减系数均小于1.表3所示为上述试验中水平、竖直两条测线6个测点的能量衰减系数β.

表3 振动能量衰减系数Tab.3 Coefficient of energy attenuation cm-1

由表3中数据可知，设置钢筋网后，水平测线上3#测点的振动能量衰减系数增大了60%，竖直方向上增大了400%.振动能量衰减到一定程度时，混凝土粒子不能液化，空间分布不再变化，对混凝土而言，振动已经失效，无法使该处的混凝土进一步密实.即：振动能量衰减系数的大小，在某种程度上反映了有效的振动能量在混凝土介质中传播距离的远近.能量衰减系数小，表示有效的振动能量可以传播更远的距离.

2.2.2 振动能量衰减系数的影响因素

目前的研究成果［5］表明：振动能量衰减系数主要与振动频率和振动延续时间有关.

(1)β值随振动频率的增加而减小，表4所示为不同振动频率下测得的振动能量衰减系数.由于能量衰减系数还和振动延续时间有关，本研究振动延续时间参照文献［8］选择60 s.由表中数据可知，振动频率相同时，设置钢筋网的混凝土能量衰减系数均小于无钢筋网的混凝土;随振动频率的增加，两种试件的能量衰减系数均有所下降.设置钢筋网的试件，振动频率提高到75 Hz时，能量衰减系数仅相当于无钢筋网试件振动频率为50 Hz.

表4 不同振动频率下的振动能量衰减系数Tab.4 Coefficient of energy attenuation under different frequency

(2)β值随着振动延续时间的延长而减小，试验测得的不同振动延续时间的振动能量衰减系数如表5所示.

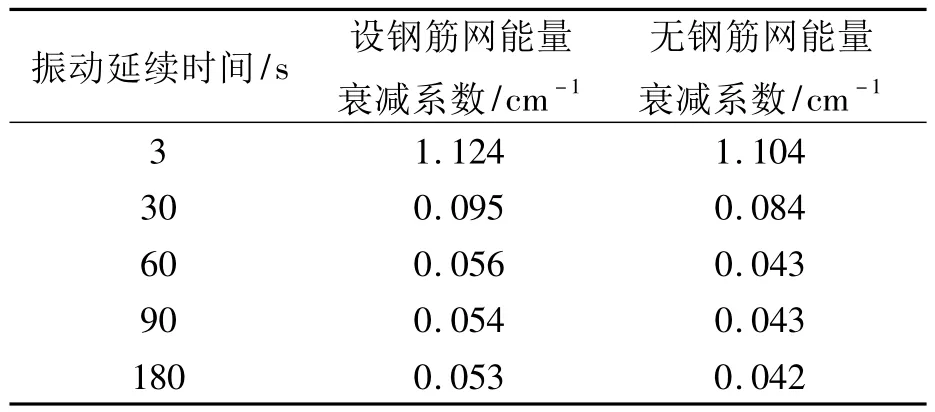
表5 不同振动延续时间下的振动能量衰减系数Tab.5 Coefficient of energy attenuation under different time

在振动开始时，能量衰减系数较大，随振动时间的延长，能量衰减系数逐渐减小.经过60 s的振动后，能量衰减系数通常就稳定下来.如表5中所述，设置钢筋网的混凝土振动开始时的能量衰减系数为1.124 cm-1，经过60 s振动后，能量衰减系数减为0.056 cm-1，在随后的120 s振动过程中，能量衰减系数只从0.056减少到0.053 cm-1.对比无钢筋网的试件，设置钢筋网后，振动延续时间增加15～30 s，能量衰减系数才相当.

从混凝土内部颗粒组成的角度看，振动施加的初期，振动波传播受到的阻力较大，能量损失严重，能量衰减系数也较大.经过60 s振动后，振捣棒有效作用半径范围内的混凝土均处于液化状态，对振动的传播阻力较小，能量衰减系数较小且较为稳定.

2.3 钢筋网上、下混凝土密度的变化

由于钢筋网对振动的阻隔作用，致使钢筋网下层混凝土不易振实.因此试件的竖直方向上，相同层厚的混凝土的密度势必有所差异.试验采用层状可拆解试模，如图6所示.测量竖直方向上不同层位的混凝土密度，从振动密实的角度来说明钢筋网对混凝土的阻隔作用.

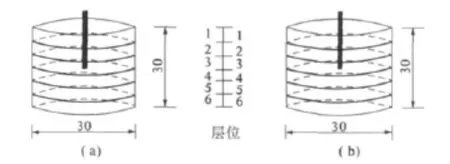
图6 层状可拆解试模Fig.6 Sandwich knock-downed mold

2.3.1 不同层位混凝土密度的测定

如图6所示，试模可平均拆解成6层，每层5 cm厚，底面直径30 cm，小于振捣棒的有效工作半径.(a)图中试模不设钢筋网，(b)图中试模中间(15 cm厚度处)焊接10 cm×10 cm钢筋网.

不同层位混凝土密度的测定步骤如下：(1)将拌合好的混凝土装入试模a，b;(2)使用振捣棒分别振动约70 s，振捣棒的插入深度为15 cm，对于设置钢筋网的混凝土，棒体下端要略高于钢筋网;(3)振实后，将表面抹平;(4)将最上层试模拆除，用长度大于30 cm的刮刀将上层混凝土铲出，称重，分别记为ma1，mb1;(5)同理依次得到ma2，mb2，…，ma6，mb6;(6)根据单层混凝土的体积计算每层的密度;(7)重复步骤1～6两次，结果取3组数据的平均值.

2.3.2 不同层位混凝土密度的试验结果与分析

依照上述方法，测得的两组试件不同层位的混凝土密度如图7所示.

由图7可知，对于上3层混凝土，设置和不设钢筋网，密度均介于2 460～2 465 kg/m3之间，层间变化趋势极其相似，即：钢筋网对其上部混凝土的振动无明显阻隔.不同的是，对于下3层混凝土，设置钢筋网的较不设钢筋网的混凝土密度有显著下降，即钢筋网对其下部混凝土的振动有较大的影响，钢筋网的存在，导致振动能量向下传播时有较大的衰减，使其下部混凝土不易振动密实.

图7 不同层位混凝土的密度Fig.7 Concrete density at different layer

3 连续配筋混凝土的振动密实

对于全厚度摊铺的连续配筋混凝土路面，首先安置钢筋支架，在钢筋支架上布置纵、横向钢筋，然后布料、振捣.因此钢筋网下部的混凝土是否振动密实，钢筋、混凝土是否紧密结合意义重大，由上文可知，钢筋网对振动能量的传播确实存在较大的阻隔作用，且振动能量衰减系数随振动频率的增加而减小，随振动延续时间的增加而减小，适当地增大振动频率、延长振动时间、减小振捣棒的间距对钢筋混凝土的振实有重要意义.

因此，对于连续配筋混凝土路面，振动密实成型时，要注意振动参数的紧密配合.与普通混凝土路面相比，适当提高振动设备的振动频率约25 Hz、延长振动时间15～30 s对提高钢筋混凝土的密实性能有重要意义.

4 结论

(1)钢筋网对振动能量在混凝土中的传播存在阻隔作用，振动能量经过单层钢筋网的阻隔，水平方向上约衰减12%，竖直方向上约衰减19%;(2)振捣棒周边的介质及介质的状态影响着混凝土粒子振动加速度的分布，对振动能量在混凝土中的传播有一定影响;(3)钢筋网的存在对钢筋网以上部分混凝土的振动密实无显著影响，对钢筋网以下的混凝土有较大影响;(4)振动频率和振动延续时间对振动的能量衰减系数存在较大影响，适当的增大振动频率、延长振动延续时间可以有效的减小能量衰减.

［1］张祖武，姚令侃.土岩界面地震波能量传递与耗散特性研究［J］.灾害学，2011，26(1)：5-8.

［2］秦厚慈，刘超英，周山.论零坍落度混凝土振动衰减规律［J］.合肥工业大学学报，1998，21(1)：97-99.

［3］SANDOR P.新拌混凝土［M］.陈志源，译.北京：中国建筑工业出版社，1990.

［4］戴俊.岩石动力学特性与爆破理论［M］.北京：冶金工业出版社，2002.

［5］VOELLMY A.High concrete quality in cold weather［J］.Rilem Symposium，1956，43：74-76.

［6］NEWLON H.Theroy of concrete slump loss as related to use chemical admixtures［J］.Design and Construction，1979，2：36-43.

［7］廖振鹏.工程波动理论导论［M］.北京：科学出版社，2002.

［8］张艳聪，王大鹏，侯子义.新拌道路混凝土最佳振动延续时间的室内试验研究［J］.公路交通科技，2010，27(11)：282-284.

［9］王建，姚令侃，蒋良潍.地震作用下土体变形破坏模式与机理［J］.西南交通大学学报，2010，45(2)：196-202.