空间喷气移动装置的姿态控制建模与仿真

刘砚菊，夏 文

(沈阳理工大学信息科学与工程学院，辽宁沈阳110159)

随着我国神州七号载人航天飞行任务的圆满完成，预示着我国成为世界上第三个独立掌握宇航员出舱活动技术的国家。出舱活动技术的掌握对于航天事业具有重大的意义与作用。宇航员在出舱活动中的主要困难是在微重力环境下的太空中，宇航员无法进行类似于在地球上的动作，无重力条件下的每一个动作都困难无比。因此，借助喷气移动装置进行舱外活动是可行的办法。文中利用坐标变换和刚体动力学原理对喷气移动装置的空间运动进行描述，建立运动学和动力学方程，并进行仿真验证。

1 喷气移动装置研究现状

空间喷气移动装置的原理是利用背包式装置紧贴宇航员的背部，装置在上下左右前后六个方向各有若干个小孔，通过小孔喷出装置内部携带的压缩气体，带动宇航员进行前进、后退、转向和姿态保持等动作。

喷气移动装置的研究主要集中在美国和俄罗斯，美国对于喷气移动装置的研究可以追溯到60年代中期，到现在为止经历了三个阶段［1］:

图1 第三代喷气移动装置SAFER

第一阶段:手持式喷气推进装置(Hand Held Maneuvering Units，HHMU);

第二阶段:载人机动装置(Manned Maneuvering Units，MMU);

第三阶段:简易EVA救援装置(Simplified Aid For EVA Rescue，SAFER)。

我国在喷气移动装置研究方面起步比较晚，但随着我国成为第三个掌握宇航员出舱活动技术的国家，这方面的研究刻不容缓。喷气移动装置的主要用途是辅助宇航员在出舱活动中进行远距离运动，建立其运动模型将为后续的研究工作打下坚实的基础。

2 喷气移动装置建模

喷气移动装置的运动模型主要由运动学模型和动力学模型两部分组成，首先利用刚体动力学建立喷气移动装置的运动学模型来描述喷气移动装置的运动状态。

2.1 运动学建模

喷气移动装置的姿态是用来描述本体坐标系相对于空间某参考坐标系的方位指向。描述卫星姿态的方法有很多，最常用的有欧拉角法和四元数法［2］。欧拉角通过坐标轴的三次旋转得到，具有明显的几何意义，且应用比较成熟，但在大角度时存在“奇异”问题;四元数法可以避免奇异，适用于大角度运动，还可以避免复杂的三角运算从而降低计算量。考虑到喷气移动装置的姿态运动主要是小角度动作，且对运动学模型的可靠性要求较高，因此文中选择了欧拉角法对喷气移动装置进行运动学建模［3］。

设定喷气移动装置本体坐标系为OXYZ，参考坐标系为OUVW，如图2所示。

图2 喷气移动装置欧拉角示意图

则由欧拉角定理可得绕XYZ三轴旋转矩阵分别为

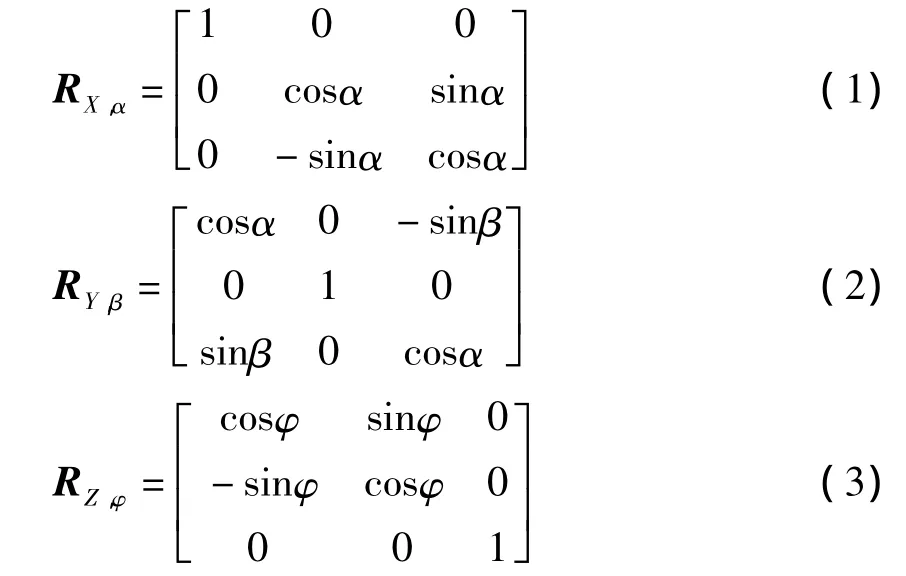
设ω为喷气移动装置绕其参考坐标系运动的角速度，则ω应是˙α，˙β，˙φ三个角速度的矢量和

由欧拉运动学方程可知

解方程(5)得

化简方程(6)得到喷气移动装置姿态运动学模型为

式中 θ=［α β φ］T，R矩阵由下式决定

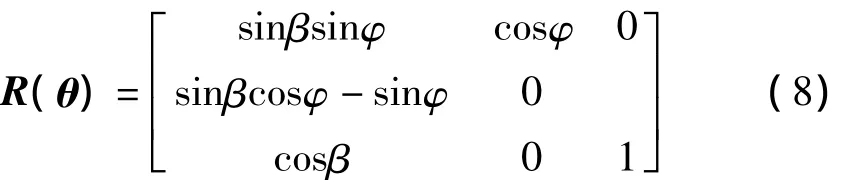
式(7)的作用是把喷气移动装置的角速度转化为欧拉角及其导数的函数，从而使动力学方程中的广义坐标转换为欧拉角坐标。通过积分运算求解出动力学方程式中欧拉角的变化规律，则可唯一地确定喷气移动装置姿态的运动规律。

2.2 动力学建模

动力学建模主要参考刚体动力学的质心运动方程，结合喷气移动装置自身的刚体运动学特性，利用矢量方程将质心加速度和喷气推力联系起来，从而描述喷气移动装置的动力学特性［3］。

喷气移动装置在参考坐标系中绕质心旋转的动力学方程为

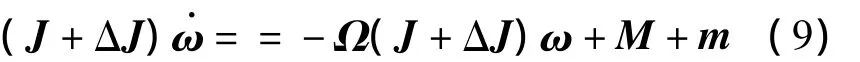
其中J∈R3×3为喷气移动装置绕质心旋转的转动惯量矩阵，ΔJ∈J3×3为该惯量矩阵由于燃料消耗等原因引起的不确定项;M=［MXMYMZ］T为定义在本体坐标系中的控制力矩;m=［mXmYmZ］T为宇航员运动时的干扰力矩。

矩阵J为

矩阵Ω为

3 运动仿真

已知喷气移动装置运动函数模型为

［4－5］，设喷气移动装置的转动惯量 J 中 JXX=43kg/m2，JYY=42kg/m2，JZZ=57kg/m2，其余项为 0;ΔJ中 ΔJXX=ΔJYY=ΔJZZ= －5kg/m2，其余项为 0;干扰力矩 m=［sint，cost，sin(2t)］T;初始角θ=［α β φ］T和初始角速度 ω=［ωX，ωY，ωX］T均为0，则:

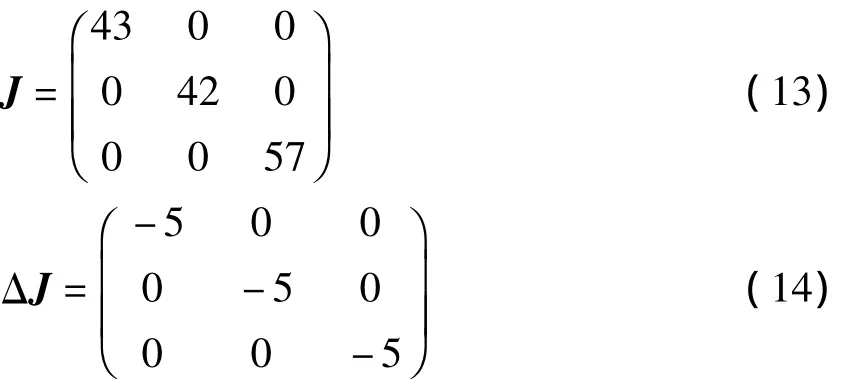
预设角度变化信号为 θf=［sint，cost，t］T，由MATLAB软件仿真得到喷气移动装置的运动曲线［5－8］，已知喷气移动装置由下向上运动，运动曲线如图3所示。

图3 喷气移动装置空间运动轨迹

图4 三轴角速度变化曲线图

图4为喷气移动装置运动过程中的三轴角速度变化曲线，曲线显示，当喷气移动装置做周期性规律运动时，三轴角速度随之进行周期性变化，对实际数据对比后可知，得出仿真数据与实际数据基本一致，证明了角速度数学模型的正确性。

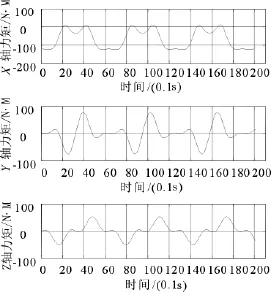
图5 三轴力矩变化曲线图

图5是喷气移动装置运动过程中的三轴力矩变化曲线，由曲线可以看出，由于喷气移动装置进行规律运动，所以三轴力矩也随之进行周期性变化，从而证明了动力学数学模型的正确性。

4 结束语

本文推导出喷气移动装置在空间运动时的运动学模型和动力学模型，并利用预设轨迹对模型进行了MATLAB仿真，主要包括运动轨迹模拟、三轴角速度变化曲线、三轴力矩变化曲线等。仿真结果验证了模型的正确性，进一步将在该模型中加入相应的算法，加强对模型的反馈控制，优化控制结构，对控制算法进行深入研究。

参考文献:

［1］陈杰.国外宇航员舱外机动装置发展综述［J］.上海航天，2000，(1):49 －53.

［2］肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2004:23 －45.

［3］吴俊伟.惯性技术基础［M］.哈尔滨:哈尔滨工程大学出版社，2000:17－25.

［4］刘金琨.机器人系统控制与MATLAB仿真［M］.北京:清华大学出版社 ，2008:494－504.

［5］王青，华莹，董朝阳，等.基于模糊变结构的空间飞行器姿态控制［J］.航空学报，2006，6:1181 －1184.

［6］John J.Craig.机器人导论［M］.负超译.北京:机械工业出版社，2006:132－142.

［7］刘延柱.刚体动力学理论与应用［M］.上海:上海交通大学，2006:76－92.

［8］许波，刘征.Matlab工程数学应用［M］.北京:清华大学出版社，2006:189－193.