基于k-最邻近分类法的灰色评估方法的改进

朱美玲，陈勇明，罗廷友

(成都信息工程学院 数学学院,成都 610225）

0 引言

在预测与决策理论中,评估是极其重要的一个环节。评估方法的种类很多,例如层次分析法、Bayes概率法、模糊评价法、聚类评估等[1],而灰色评估是评估中较为重要的一种。

在评估的研究过程中可以发现,观测矩阵是评估的主要依据,是评估的出发点。观测矩阵主要有两种形式:一是客观数据,二是专家评分。本文中我们将第二种观测矩阵称为专家评分矩阵。现实生活中有很多这样的例子,如企事业单位的人才招聘,在面试环节往往由有经验的员工出任考官考察应聘者的专业知识技能、人际关系处理能力、创新能力以及工作态度等各方面的指标,然后利用考官们对各指标的评分进行评估以确定是否录取应聘对象。对于这类专家评分问题,评价主体——专家在评分过程中往往带有自身的主观倾向,如某些专家打分较为保守,对所有对象评分值普遍偏低;同时另一些专家打分又习惯性偏高。而以往的灰色评估方法,无论是经典的灰色聚类评估的主要方法白化权函数和关联度,还是近年来的一些新的灰色评估方法或者灰色评估方法的改进[2～4]，都没有考虑到这一点,即在评估过程中没有考虑如何消除专家主观因素对结果的影响。针对这一问题,本文拟借鉴k-NN方法,利用每位专家以往的评分记录修正其当前评分矩阵,消除评分时存在的主观倾向,使评估更趋于客观与合理。

1 预备知识

1.1 k-NN的基本原理

定义[5]k-NN(k-Nearest-Neighbor)即k-最邻近分类法,是数据挖掘中常用的一种算法:在观测数据集中动态的确定k个与我们希望分类的新观测相类似的观测,并使用这些观测把新观测分到某一类中。

在使用k-NN方法时,需要先确定一个适当大小的k值。如果k值选取过小,如k=1,则分类方式将对数据的局部特征非常敏感;如果k值选取过大,如k=n(其中n是观测数据集中观测的总数),则相当于对大量数据取平均值,同时平滑掉了因单个数据点的噪声而导致的波动性[5]。因此选择适当的k值是非常重要的。

1.2 灰色关联度

定义[6]设系统行为序列S=(s1,s2,…sm),以及

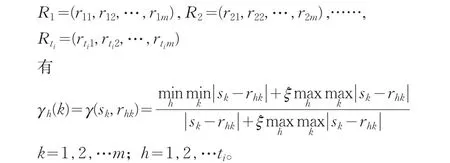
其中，ξ∈(0,1),称为分辨系数。γh(k)=γ(sh,rhk)表示向量S的第k个分量与Rh第k个分量的关联度,令

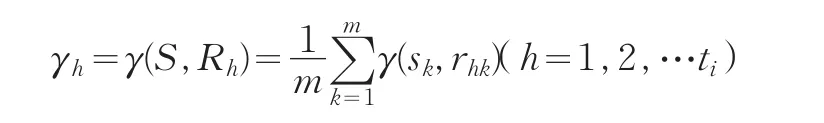
对所有的h=1,2,…,ti计算出γh,得向量：

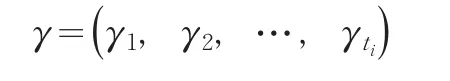
这里,γh称为Rh与S的灰色关联度。

1.3 问题的一般描述

需要考虑的问题的一般描述如下：

设评分主体为某专家组,用集合E={E1,E2,…,Ek}表示;考核指标用集合I={I1,I2,…,Im}表示;当前被考核对象用集合A={A1,A2,…,An}表示。另设专家Ei有ti次历史评分记录,将评分值以及相应的最后聚类结果制成表格。不失一般性,为了便于书写我们此处将评分值的取值范围定义为区间[1,10]上的整数,基于评分值的聚类标准为:当8≤rhj≤10时,指标Ij归属于①类等级;当5≤rhj≤7,指标Ij归属于②类等级;1≤rhj≤4,指标Ij归属于③类等级,评分值越高对应的类越令人满意,即①类优于②类,②类优于③类。根据上述规定,制作表1。将第u(u=1,2,…,n)个当前考核对象的评分数据制成表2。

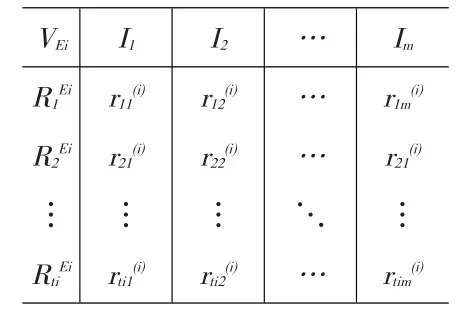
表1 专家Ei历史评分数据

表2 第u个当前考核对象评分数据

则相应的当前评分矩阵为：

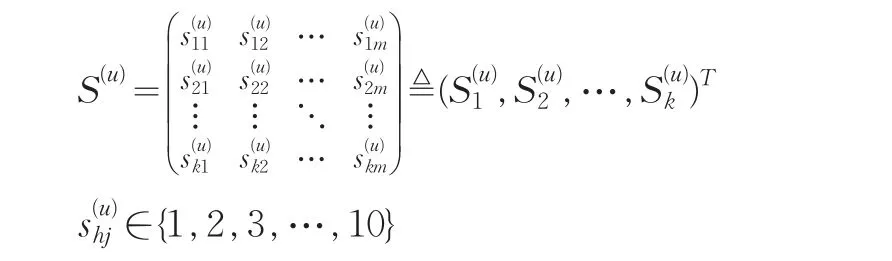
2 基于k-NN方法对当前专家评分矩阵修正的算法和基本原理

2.1 算法的基本原理

为了修正当前被考核对象的专家评分矩阵,首先我们利用关联度来度量在每位专家的历史评分数据与其对当前被考核对象Au评分数据的相似度,并选出个数适当的最相似历史数据,这样做是因为利用最相似历史数据而不是全部历史数据来修正当前专家评分向量,所得的结果将更趋于客观、合理;其次我们构造修正函数,根据筛选出的每位专家的最相似历史数据修正其当前评分向量,从而得到修正的专家评分矩阵,继而进行评估。

2.2 算法

首先,根据关联度来度量在每位专家以往的评分数据与其对当前被考核对象Au评分数据的相似度。

由表1专家Ei的ti次历史评分数据,我们得到ti个序列(即专家Ei的ti次历史评分向量):

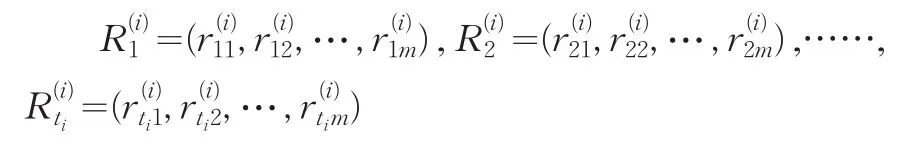
另外有专家Ei对被考核对象Au当前评分向量:

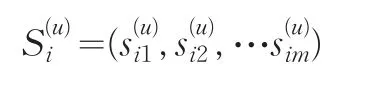
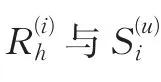
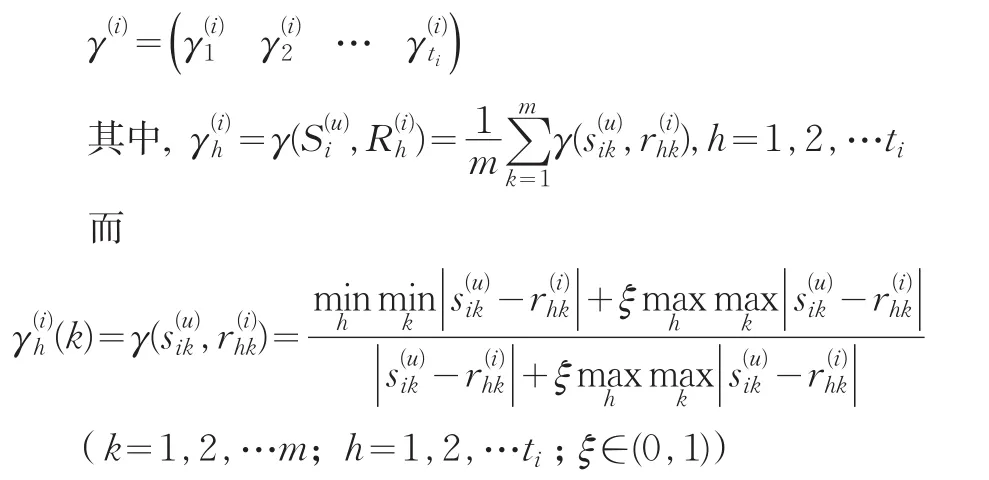
根据要求取临界值γ0,筛选出专家Ei的历史评分数据中与其对当前考核对象Au评分向量最接近的数据。

经过上述计算后对专家Ei可以得到ki个与当前评分向量相近的历史评分向量。这里我们借鉴k-NN方法对每个专家Ei利用关联度从其过去的ti次评分记录中找到与当前评分最为接近的ki个评分;与其不同的是我们并不事先确定ki值,而是利用关联度选择适当的数据后,得到ki的取值。根据k-NN方法对k值的考虑,我们得到ki值以后,根据其大小适当的修正关联度的临界值，以保证ki值不是过大或者过小。设修正后ki调整为。将个数据按照取出的顺序排列,仍记为仿照表1的做法,我们制作表3

由前文所述知,表3中元素(即评分值)的取值范围是1到10的整数,表中⊗是某次考核对某指标经专家组聚类评价后最后划分所至的类,⊗的取值是①类、②类或者③类。

将规定的评分值(这里是1到10的正整数)作为列,将规定的类作为行,以评分值在各类出现的次数作为元素,绘制成表4。例如表4中第一行第一列元素n1,1表示表3中评分值为1最后被分至①类的次数,其他以此类推。

下面构造修正函数。构造函数时我们只考虑评分值规定的所属类别与最终被划分到的类别是相邻的。因为实际情况下参加考核的专家具有较为丰富的经验,对评分的划分标准有较好的把握,因此不同专家评分时一般不会出现对同一被考核对象给出差异悬殊的评分。构造修正函数如下：

表3 筛选后专家Ei的个相似评分数据

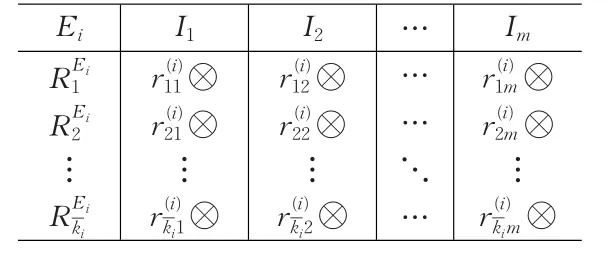
表3 筛选后专家Ei的个相似评分数据

Ei I1 I2 Im REi 1 REi 2⋮r(i)11⊗r(i)21⊗r(i)12⊗r(i)22⊗r(i)1m⊗r(i)2m⊗⋮⋮⋮REi-ki r(i)-ki1⊗r(i)-ki2⊗………⋱…r(i)-kim ⊗

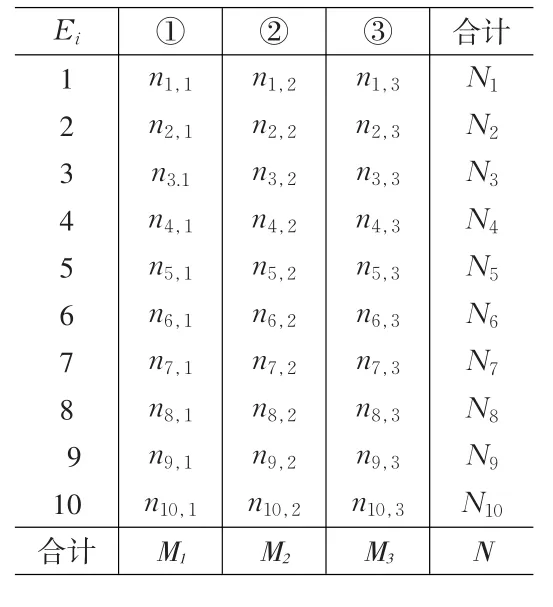
表4 专家Ei相似评分数据按类的次数分布

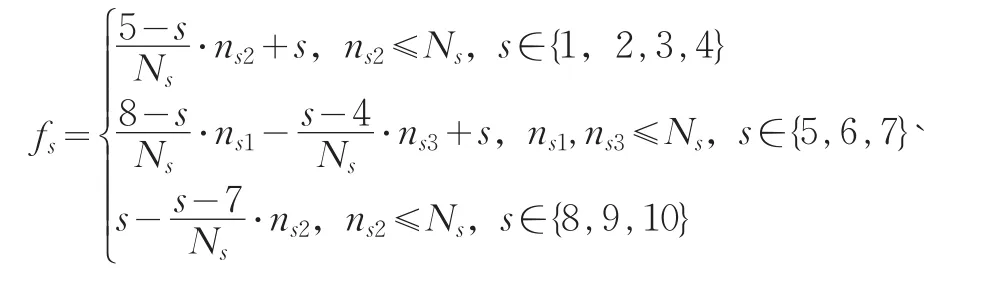
其中,对评分值s修正时s已经确定,不作为变量存在于函数中,fs是对s修正后的评分值,Ns即表4最末一列的元素,即行元素之和,ns1、ns2和ns3为表4中的元素。

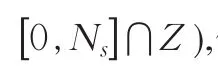
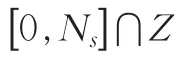
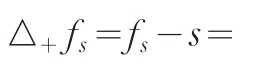
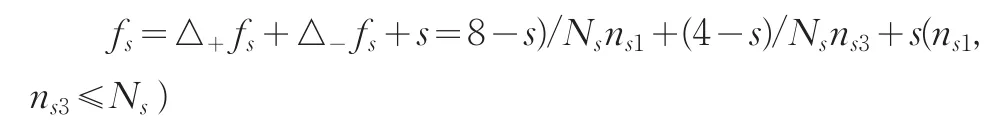
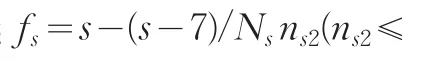
3 算法的一般步骤

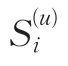
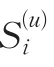
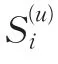
4 算法实例

设有三个专家对被考核对象的四个指标进行评分,评分标准与前文一致:评分值的取值定义为在区间[1,10]上的整数,基于评分值的聚类标准为:当8≤sj≤10时,指标Ij归属于①类;当5≤sj≤7,指标Ij归属于②类;1≤sj≤4,指标Ij归属于③类(通常评分值越高对应的类越令人满意)。则专家组用集合E={E1,E2,E3}表示,被考核对象用集合A={A1,A2}表示;考核指标用集合I={I1,I2,I3,I4}表示。先计算被考核对象A1修正的专家评分矩阵,依照同样方法可以得出A2的修正评分矩阵。

专家E1,E2,E3对被考核对象A1关于指标I1,I2,I3,I4的评分矩阵为：

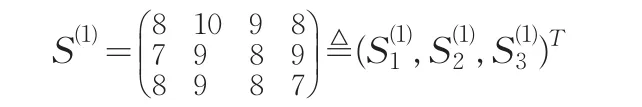
表5、6、7中的第一行表示指标;第一列表示历史数据的次数标识;表中元素分为上下两部分,上面部分是专家评分值,下面部分是最终该指标被划分的类。

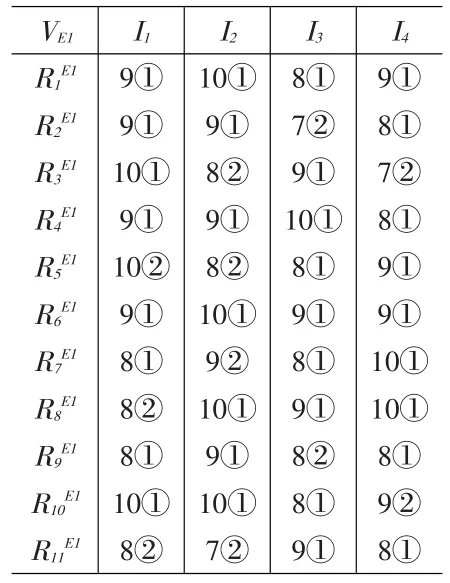
表5 专家E1历史数据

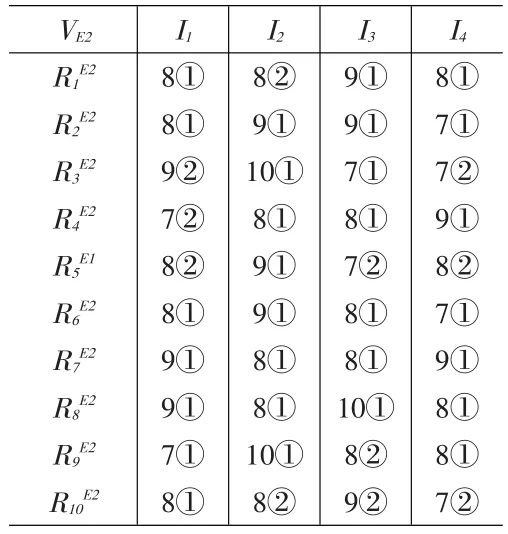
表6 专家E2历史数据

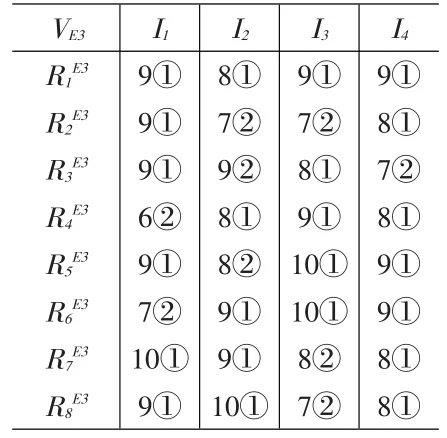
表7 专家E3历史数据

进行计算（k=1,2,3,4;h=1,2,…,11）。取ξ=0.5,计算得

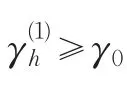
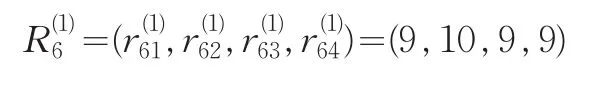
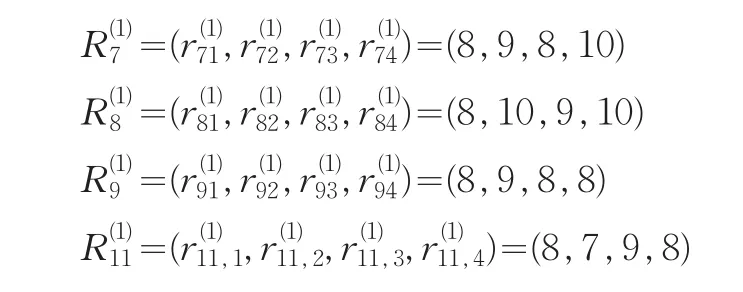
第三步,计算修正的专家评分矩阵。得到的向量个数为k1=5,历史数据总数n1=11,则不需对k1进行必要的修改。故根据筛选出来的历史评分向量将表5缩减成表8。

将表8中出现的评分值作为列,将表8中出现的类作为行,以评分值在各类出现的次数作为元素,绘制成表9

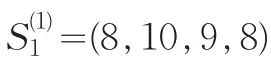
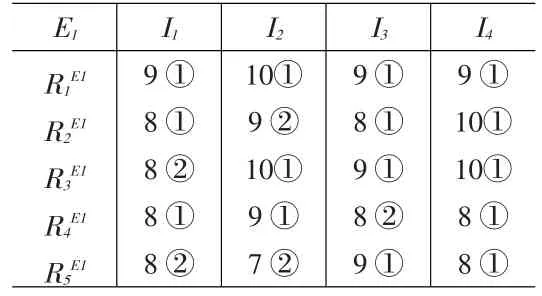
表8 专家E1历史评分与S1的最相似数据

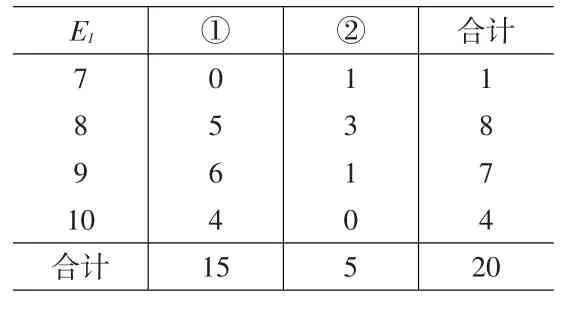
表9 专家E1相似评分数据按类的次数分布

依据同样方法，计算E2对A1的当前评分向量S2=(7,9,8,9)的修正评分向量,关联向量临界值取γ0=0.8时k2=1,由于k2取值过小,调整关联向量临界值γ0=0.7,则k2相应的调整为=4,修正评分向量为E3评分向量S3=(8,9,8,7)的修正评分向量,关联向量临界值取γ0=0.8时k3=1,由于k3取值过小,调整关联向量临界值γ0=0.5,则k2相应的调整为=4,修正评分向量为

第四步,得到专家E1,E2,E3对被考核对象A1关于指标I1,I2,I3,I4的修正的专家评分矩阵为：

专家E1,E2,E3对被考核对象A2关于指标I1,I2,I3,I4的评分矩阵为：

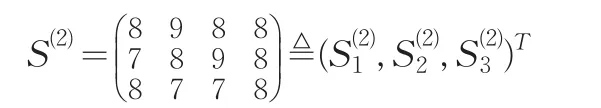
完全依照上面的处理方法,我们得到S(2)修正的专家评分矩阵：

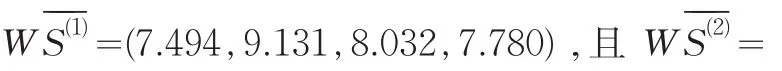
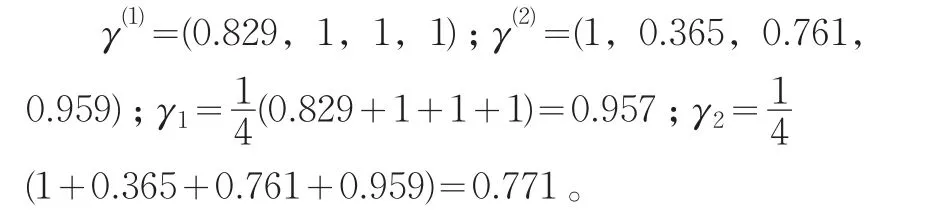
显然γ1＞γ2,故被考核对象A1优于被考核对象A2。

5 结语

基于k-NN对专家评分矩阵进行修正,以消除专家评分时的主观倾向（即习惯性偏高或者偏低）可以使得评估的结果更趋于客观化、合理化。另外值得一提的是,利用本方法得出被考核对象之间的聚类系数更具有可比性。

[1]徐玖平,陈建中.群决策理论与方法实现[M].北京：清华大学出版社,2009.

[2]党耀国,刘思峰.灰色综合聚类[J].统计与决策,2004，(10).

[3]李宜敏,罗爱民,吕凤虎.灰色聚类评估的一种改进方法[J].统计与决策,2007，(1).

[4]王育红,党耀国.基于D-S证据理论的灰色定权聚类综合后评价方法[J].系统工程理论与实践,2009,29(2).

[5]K.P.Soman,Shyam Diwakar,V.Ajay.数据挖掘基础教程[M].北京:机械工业出版社,2009.

[6]刘思峰,党耀国,方志耕,谢乃明.灰色系统理论及应用（第五版）[M].北京：科学出版社,2010.