小型化谐波抑制双模方形贴片带通滤波器

金秀梅， 李民权， 刘 坤， 孙家训

（安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039）

在现代无线通信系统中——特别是在射频和移动通信系统中，结构紧凑的高性能带通滤波器扮演着越来越重要的角色。随着集成电路的发展，无线通信设备日趋小型化，加之频谱资源有限，更加迫切需要小型化、通带损耗低和带外谐波抑制度高的带通滤波器［1－2］。近年来，小型化和低损耗成为人们争相研究的热点，可以使滤波器固有阶数减半的双模滤波器备受关注。因此，各种结构的双模滤波器应运而生［3－10］，如方形贴片、圆形贴片、三角形贴片和微绕环状谐振器结构的双模滤波器。文献［3］首次提出将双模的理念应用到平面滤波器设计中，并成功设计出双模带通滤波器。双模滤波器主要是在单腔谐振器中利用微扰结构产生一对简并模，在实际电路中可以等效为双调谐电路，即单腔同时可以产生2个谐振频率点，通过微扰的形式使得这2个频率适当地分离并相互耦合［4－5］。

本文采用较大介电常数的高频PCB介质板材，运用L形输入输出谐振器。在方形贴片上嵌入方块状腐蚀结构作为微扰源，设计了一种方形贴片开十字交叉槽和开矩形窗口的双模带通滤波器。这种开槽结构有效地增加了基波的电流路径，同时可使二次谐波的电流路径保持不变，不仅有效加大了2种模式的隔离度，而且实现了滤波器的小型化。仿真结果表明，该滤波器性能良好，通带两侧产生了2个传输零点，大大提高了带外的抑制度；L形馈电结构也可引入一个传输零点，很好地延迟了寄生通带，可使寄生通带出现在3倍频之后。

1 滤波器设计

1.1 单模结构谐波抑制带通滤波器的设计

图1所示为开槽处理的单模带通滤波器平面拓朴结构，即在传统的方形贴片单模谐振器上开2个十字交叉缝隙，输入／输出端采用L形谐振臂。为了减小滤波器的体积，对L形谐振臂进行适当的弯曲处理。之所以采用十字正交开缝和L形谐振器，是为了引入传输零点，提高滤波器的带外选择性能［7－8］，以获得较好的带外谐波抑制度。

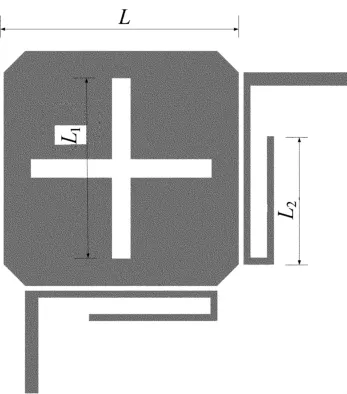
图1 单模结构带通滤波器平面结构

利用Ansoft公司的基于电磁场有限元方法的高频电磁仿真软件HFSS对其进行三维建模，介质基板采用RogersRT6101，其介电常数为10.2，厚度h＝1.2mm，铜箔厚度0.035mm。滤波器的输入／输出端口阻抗为50Ω；正方形贴片的边长为L，矩形槽的长度为L1，正方形微扰切槽的边长为t。输入／输出谐振臂与贴片间的距离为0.2mm，改变谐振臂与方形贴片之间的距离可以相应地改变带通滤波器的耦合度。为了减小插损，方形贴片的4个拐角做切角处理。

图2所示展示了不同槽线长度L1对应于不同基模的谐振频率，同时通过适当调整槽线长度L1可相应地引入传输零点，控制带外的谐波，而槽线长短的变化对高次谐波分量几乎没有影响。随着槽线长度L1的增加，带通滤波器的基波谐振频率相应地降低，与传统方形贴片双模滤波器相比，可以通过此方法减小滤波器体积，故选择适当的槽线可以使方形贴片滤波器实现小型化和良好的谐波抑制。

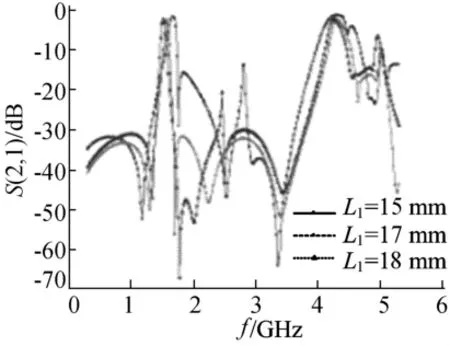
图2 不同缝隙长度下的滤波器S（2，1）参数

1.2 双模结构谐波抑制带通滤波器的设计

谐波抑制方形贴片双模带通滤波器的平面结构如图3所示，采用输入／输出端正交馈电结构、方形贴片切角形式以降低损耗；L形馈电臂引入传输零点以增加带外谐波抑制；贴片开十字正交槽线以实现小型化和谐波抑制；通过细槽线链接的2个方形切槽对角排列作为微扰源，产生一对正交化简并模式。采用这种结构的双模谐振器很好地实现了小型化和通带外高次谐波抑制，性能明显优于传统方形贴片双模滤波器［11］。

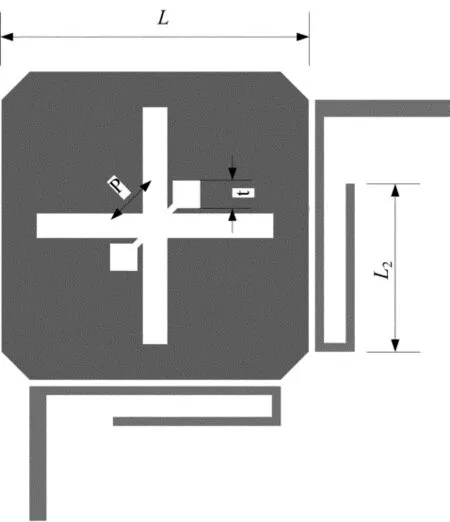
图3 双模结构带通滤波器平面结构

2 仿真结果及分析

借助三维电磁仿真软件HFSS11进行辅助设计，其三维模型的主要尺寸见表1所列。

表1 带通滤波器主要结构尺寸 mm

图4所示给出了变量L2的不同取值情况下，双模带通滤波器的S（2，1）图形，选择合适的L2值可以在通带外相应地引入传输零点，得到较好的带外谐波抑制度。

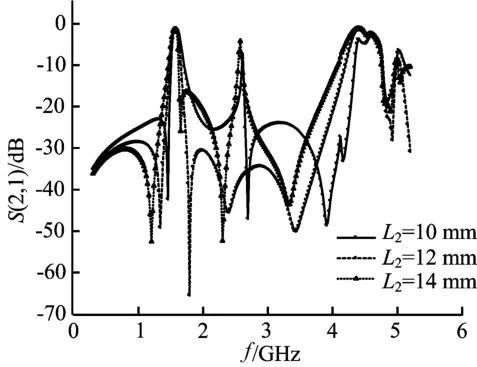
图4 不同L2长度下的滤波器S（2，1）参数

通过软件的多次仿真优化，双模带通滤波器的S参数曲线如图5所示。仿真结果表明，所提出的双模带通滤波器性能优越，中心频率为1.56GHz，带内最大插损小于1.5dB，带外谐波抑制良好，谐波被抑制到－30dB以下，寄生通带被推移到基波的3倍频以外，谐波中心频率出现在4.7GHz左右，所提出的滤波器性能优于文献［7］中提出的滤波器。

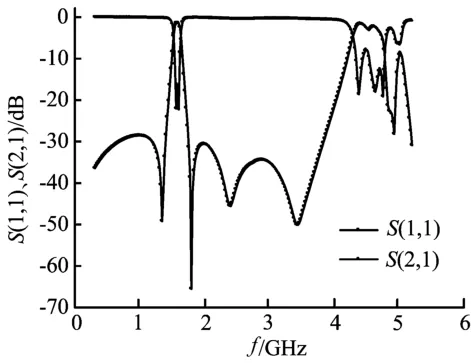
图5 滤波器仿真结果

3 结束语

本文在传统平面微带方形贴片双模谐振器的基础上，提出一种开有十字交叉槽的贴片谐振器结构；通过开方孔添加微扰的方式和设置L形馈电输入／输出的模式，结合十字交叉槽引入传输零点，实现了一款性能良好的小型化谐波抑制双模带通滤波器；具体分析了该滤波器的工作机理和结构参数对其特性曲线的影响规律。它可以应用于平面微波电路的设计当中，并对无线通信系统中滤波器的研究与设计具有较大的参考价值，应用前景十分广阔。

［1］李俊鹏，杨明武.一种含镜频抑制作用的微带发卡滤波器的设计 ［J］.合肥工业大学学报：自然科学版，2009，32（4）：550－552.

［2］王 凯，李 楠，杨明武.基于FDTD算法的环状蝶式双模滤波器［J］.合肥工业大学学报：自然科学版，2007，30（7）：908－911.

［3］Wolff I.Microstrip bandpass filter using degenerate modes of a microstrip ring resonator［J］.Electronics Lett，1972，8（12）：302－303.

［4］黄晓东，程崇虎.直接馈电的小型化微带双模带通滤波器［J］.微波学报，2010，26（3）：52－55.

［5］Gorur A.Description of coupling between degenerate modes of a dual－mode microstrip loop resonator using a novel perturbation arrangement and its dual－mode bandpass filter applications［J］.IEEE Transactions on Microwave Theory and Techniques，2004，52（2）：671－677.

［6］Kuo J T，Chen S P，Jiang M.Parallel－coupled microstrip filters with over－coupled end stages for suppression of spurious responses ［J］.IEEE Trans Microw Wirel Compon Lett，2003，13：440－442.

［7］Singh Y K，Chakrabarty A.Miniaturized dual－mode circular patch bandpass filters with wide harmonic separation［J］.IEEE Trans Microw Wirel Compon Lett，2008，18（9）：584—586.

［8］Griol A，Mira D，Marti J，et al.Microstrip side－coupled ring bandpass filters with mode coupling control for harmonic suppression［J］.Electron Lett，2004，40：943－945.

［9］Tu W H，Chang K.Miniaturized dual－mode bandpass filter with harmonic control［J］.IEEE Microw Wirel Compon Lett，2005，15：838—840.

［10］Li J Y，Chi C H，Chang C Y.Synthesis and design of generalized Chebyshev wideband hybrid ring based bandpass filters with a controllable transmission zero pair［J］.IEEE Transactions on Microwave Theory and Techniques，2010，58（12）：3720－3731.

［11］Hong J S，Lancaster M J.Microstrip filters for RF／Microwave applications［M］.New York：Wiley，2001：404－420.