基于垂向振动的车体加速度分析

张 馨，李 会

(1.唐山轨道客车有限责任公司，河北唐山 063035;2.大连交通大学，辽宁大连 116028)

随着铁路货运向重载方向发展，我国大秦线路开行了2万t重载列车。C80B型敞车为大秦线专用运煤敞车，运营过程中车体钢结构过早地出现破损问题，车体关键部位的疲劳开裂现象明显增加，如:车体枕梁内侧、上心盘顶面与中梁内侧顶面、侧柱与侧板相交处等关键部位出现裂纹，其主要原因为车辆运行过程中的振动造成的疲劳破坏。车辆振动时的大部分能量集中在低频振动，也就是车体浮沉、滚摆、点头、摇头等基本形式的典型振动组合的复杂振动。这就有必要考虑车辆运行过程中的典型振动对车体动态性能的影响。

从目前研究情况看，对车辆垂向力的研究大多单纯停留在静态分析水平，很少考虑车辆的典型振动对车体动响应的影响问题。车辆在实际运行中主要受轨道不平顺的激励，是产生车辆各种振动的主要根源。轨道垂向不平顺会引起车辆的点头振动和滚摆振动，同时又会引起轮重波动，不但增大轮轨垂向力和车体垂向加速度，而且影响线路的稳定性，降低运行的平稳性与安全性。车辆的运行平稳性就是指车辆在钢轨上运行时的平稳程度。车辆的运行平稳性通常用“平稳性指标”或“振动加速度”来评定。因此，从垂向激励引起的典型振动入手，采用结构动力学理论和有限元分析技术，建立C80B型敞车整车有限元模型，以轨道垂向不平顺作为动力学边界条件，模拟计算车辆在不同轨道激励频率下发生的典型振动，并进行动响应计算，获得车体关键部位的动响应时间历程，分析车体关键部位的加速度。然后根据波长和频率的对应关系，通过改变激励波长设计不同频率的轨道不平顺，进一步探讨轨道激励频率对车辆运行稳定性的影响。

1 建立模型

1.1 建立整车有限元模型

由于分析的是整车的振动特性，需要设计适当的轨道载荷激励作用于轮对使车辆发生典型振动，因此需要建立包括车体和转向架在内的整体结构模型。建立C80B型敞车模型包括转向架及车体底架、侧墙、端墙等结构。转向架采用四面体实体单元来模拟，车体底架、侧墙、端墙等结构均使用四边形薄壳单元来模拟，划分有限元网格为37 626个，节点为25 323个。整车有限元模型见图1。

图1 C80B型敞车整车有限元模型

1.2 载荷模型

车辆振动时的大部分能量集中在低频振动，这种振动是由基本的典型振动组合而成的复杂振动。在进行模态分析的基础上，确定了轨道激励频率的范围，激励频率选择在0.5～4 Hz的12个频率。轨道不平顺的函数形式用具有代表性的正弦函数作为激励［1］。通过改变激励频率，用12个不同频率的正弦激励作为轨道激励作用于轮对，进行动响应分析得到哪些频率对车体的动应力有影响。轨道不平顺的波形、波长、幅值、速度及线路状态是设计轨道激励的关键因素。轨道波形见图2。

图2 轨道波形

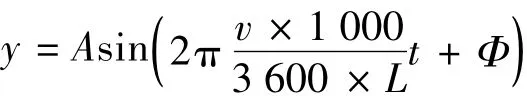
式中:y为波形;A为轨道不平顺的幅值;v为通过速度，取120 km/h;Φ为轨道不平顺的相位，两股钢轨取同相位;t为时间，设为60 s;L为轨道不平顺的波长。

幅值、速度及线路状态的确定:假设轨道状态为长度2 000 m的直线轨道，货车车辆(C80B)以速度v=120 km/h在单一谐波不平顺激扰作用下行驶，根据我国《铁路线路维修规则》［2］，轨道不平顺值的最小极限值IRmin=4 mm，最大极限值为IRmax=9 mm。根据京沪线下行轨检车采样数据测得，经过约5万t运量，实测轨道平均下沉4.41 mm［3］。所以本文假设轨道高低随机不平顺幅值A在0～5 mm范围内变化。

轨道上存在着各种波长的不平顺，从数十毫米到数米甚至数十米，甚至超过百米的波长都存在，本文参考货车不平顺的不利波长为10～20 m［4］。由频率公

表1 轨道激扰频率波长关系

综上所述，根据表中频率和波长的关系设计波形，会得到12组不同频率的轨道激励模式，按照模拟车辆点头和滚摆振动的线路形式分别作用于对应的轮对，进行动响应计算，即可获得车体关键部位的动响应，进行动响应分析。

2 振动过程动响应分析

模拟车辆在设计的典型线路上运行，考察设计线路上车体的主要振动形式，讨论振动过程中车体的弹性表现，分析车辆振动过程不同振动形式对车辆稳定性的影响，探讨轨道激励波长对运行稳定性的影响。

2.1 确定振动形式

模拟的轨道激励的目的是使车体发生垂向典型振动，为了验证振动形式，查看振动过程位移时间历程对应的位移云图，图3为不同频率的轨道不平顺线路行驶，模拟的2种轨道形式下的车体位移云图。

图3 振动过程位移云图

从位移云图3可知，模拟的轨道激励使车体发生了滚摆和点头振动，说明设计的激励模型是可行的。

2.2 车体加速度分析

加速度是评定车辆运行稳定性的重要指标，下面对2种振动过程的加速度进行分析，探讨不同的垂向振动对车辆运行稳定性的影响。图4为点头振动过程中车体枕梁处节点加速度时间历程。

由图4可以看出，车体枕梁加速度曲线成周期变化，随着激励频率的升高，周期数量增多，加速度幅值增大。频率为1.5 Hz时，加速度最大值为1.7 m·s-2;频率为2.4 Hz时，加速度最大值为6 m·s-2;根据货车运行品质标准及评定，车体垂向加速度小于2 m·s-2时为优等;在2.0～3.5 m·s-2为良好;在3.6～4.5 m·s-2为满意;在4.6～6.5 m·s-2为容许;6.5 m·s-2时不能长期运用，属于强度不利的条件;大于7.0 m·s-2时长期运用存在危险，有损车辆强度。上述2个激励频率产生的加速度均在可以接受的范围，没有达到破坏的程度，对车体来讲是安全的。但是激励频率在2.4 Hz时，加速度6 m·s-2有些高，应该引起注意，说明此频率的激励对车体的影响很大。下面进一步探讨2种振动过程车体枕梁、底架中心点、底架角点加速度与激励频率的关系，图5为车体枕梁节点加速度绝对值与激励频率在2种振动下的数值关系图。

图4 点头振动枕梁节点加速度

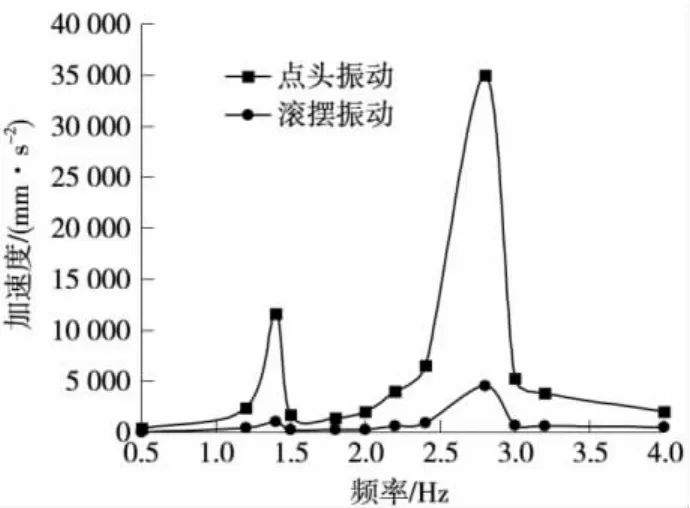
图5 枕梁节点加速度-频率关系

由图5可知，2种振动过程，车体枕梁加速度随着激励频率的升高幅值增大，加速度曲线随频率的变化趋势相近，均在1.4、2.8 Hz时出现峰值，加速度最大值出现在2.8 Hz。点头振动的最大加速度为36 m·s-2，已经大大超出安全范围，车体在此条件下属于危险运行，对车体强度破坏很大。滚摆振动最大加速度为4.8 m·s-2，没有超出安全范围，货车运行品质评定为容许。激励频率在1.2～1.5 Hz、2～3.0 Hz时加速度上升明显，这几个频率对车体强度影响非常大，车体枕梁加速度对这几个激励的频率比较敏感。图6、图7为车体底架中心节点和底架角点加速度-频率关系。

图6 底架中心节点加速度-频率关系

图7 底架角点加速度-频率关系

由图6、图7可知，车体不同部位的加速度与激励频率变化关系基本接近，各部位加速度幅值不同，点头振动加速度幅值在考察频率范围内均大于滚摆振动加速度的幅值，2种振动加速度幅值随激励频率的变化趋势基本一致。2种振动情况下，车体关键部位加速度幅值随着激励频率的升高增大。点头振动车体中心加速度最大值出现在4 Hz，最大加速度为2.4 m·s-2，没有超出安全范围，货车运行品质评定为良好。车体底架角点加速度最大值出现在2.8 Hz，最大加速度为58 m·s-2，已经大大超出安全范围，车体在此条件下属于危险运行，对车体强度破坏很大。滚摆振动中心点加速度最大值出现在4 Hz，最大加速度为0.24 m·s-2，没有超出安全范围，货车运行品质评定为优等。车体底架角点加速度最大值出现在2.8 Hz，最大加速度为15 m·s-2，超出安全范围。上述情况是模拟轨道理想化的情景，在实际中不可能出现，但是在1.2～1.5 Hz、2～3.0 Hz的激励是特别需要注意的，即在速度为120 km/h时，11.11～16.67 m、22.22～27.78 m的轨道波长是需要注意避免的。

3 结论

从模拟车辆发生垂向振动入手，对振动过程车体的加速度进行分析。通过改变轨道激励频率的方式，探讨车体关键部位加速度与激励频率的关系，得出以下结论。

(1)设计的轨道载荷达到预想结果，车体点头和滚摆振动发生。

(2)2种振动对车体加速度的影响不同。点头振动对加速度的影响比滚摆振动剧烈得多。结合实际车体破损情况，车辆在线路运行过程可能发生点头振动比较多。

(3)车辆发生垂向振动时，车体加速度随激励频率升高幅值增大，周期数增多。频率在2.0～3 Hz时对车体加速度影响很大，激励频率在2.8 Hz时对车体的影响最大，加速度达到最大值，是与车辆自振频率耦合的结果，在设计中要考虑避免这种频率的激励。

［1］翟婉明.车辆-轨道耦合动力学［M］.北京:科学出版社，2007:12-73.

［2］练松良，黄俊飞.客货共运线路轨道不平顺不利波长的分析研究［J］.铁道学报，2004，26(2):111-115.

［3］严隽耄.车辆工程［M］.北京:中国铁道出版社，2003:405-451.

［4］鲁寨军，田红旗，周 丹.270 km/h高速动车模态分析［J］.中国铁道科学，2005，26(6):18-23.

［5］王福天.车辆系统动力学［M］.北京:中国铁道出版社，1994:89-102.