CRTSⅡ型板式轨道轨道板温度测量与变形分析

韩志刚，孙 立

(中铁第四勘察设计院集团有限公司，武汉 430063)

CRTSⅡ型板式无砟轨道由钢轨、弹性扣件、预制轨道板、水泥沥青砂浆调整层、连续底座板(桥梁)或支承层(路基)、滑动层(桥上)、侧向挡块(桥上)等部分组成。如图1所示。

图1 桥上CRTSⅡ型板式无砟轨道结构示意

在CRTSⅡ型板式无砟轨道结构中，水泥沥青砂浆层作为轨道板和混凝土底座或支承层之间的垫层材料，起到填充、调整轨道结构高度、支撑承力并传力作用，并可以为轨道板提供一定的刚度、弹性和韧性。水泥沥青砂浆的性能直接影响到列车运行品质、轨道结构耐久性以及运营维修成本，他是高速铁路建造的关键工程材料之一。

目前在CRTSⅡ型板式无砟轨道施工过程中发现，轨道板与水泥沥青砂浆存在离缝现象，离缝主要出现在轨道板4个边角位置。如图2所示。

图2 轨道板与水泥沥青砂浆层离缝

初步分析离缝是由于轨道板沿其厚度方向不均匀温度梯度引起的;因为刚施工完毕水泥沥青砂浆层，轨道板没有承受列车载荷作用;当轨道板均匀升温时，会引起轨道板沿其长度和宽度方向的伸长变形;当轨道板均匀降温时，会引起轨道板沿其长度和宽度方向的收缩变形;而当轨道板沿其厚度方向存在温度梯度时，会使得轨道板产生竖向的翘曲变形。

轨道板与水泥沥青砂浆层的离缝不仅会加快水对轨道板的侵蚀，加速砂浆裸露部位的破损脱落，而且也会对将来的行车造成安全隐患。

本文基于Ansys有限元软件建立轨道板温度梯度分析模型，以试验测量的轨道板温度和变形为初始分析条件，分析不均匀温度梯度对轨道板翘曲变形的影响，通过实测轨道板变形结果与数值模拟结果的对比，验证有限元分析模型的可靠性，并为CRTSⅡ无砟轨道板的结构设计及优化提供参考。

1 轨道板温度、变形测量

1.1 轨道板传热性能概述

CRTSⅡ型轨道板为钢筋混凝土结构，其传热性能存在明显滞后现象。当轨道板被太阳照射，其结构表面温度迅速上升，但内部大部分区域仍保持原来的温度状态，会在轨道板厚度方向形成不均匀的温度梯度。轨道板的温度梯度变化不仅与其朝向、日照直射强度和日照时间有关，而且与环境温度有关。

1.2 轨道板温度观测

轨道板内部温度梯度的分布情况一直是设计者最关注的问题，本次试验只对轨道板表面和底面进行测量。其中采用4个测温电偶测量轨道板板底温度，4个测量点分别位于板端、中间位置其分布如图3所示。采用红外测温枪测量轨道板表面温度。

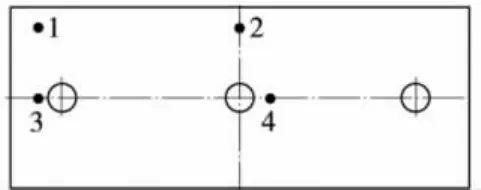
图3 板底温度测量点分布示意

轨道板板底温度采用4个测温电偶的平均值，测量数据如图4、图5所示，(8月份测量某块轨道板，板底面和表面温度与时间变化关系)，从图中可以得到以下结论。

(1)轨道板底面与表面的温度随日照、环境温度和时间的变化而变化;轨道板表面从2:00～13:00处于升温状态，最高温度为51.2℃，从13:00～2:00处于降温状态，最低温度为30.8℃;轨道板底面温度变化幅度远小于板表面温度变化幅度，而且升温、降温滞后于轨道板表面，从6:00～16:00处于升温状态，最高温度为40.6℃，从16:00～6:00点处于降温状态，最低温度为30.8℃。

(2)轨道板表面、底面温度差的变化与板表面温度变化情况基本一致，从4:00～13:00温度差逐渐增大，最大正温差为12.4℃;从13:00～4:00温度差逐渐减小，最大负温差为-5.5℃;同时，在一天内出现2次零温差(板底面温度与板表面温度相同)，分别出现在早上6:00和下午16:00。轨道板表面与底面温差变化幅度在-5.5～12.4℃，轨道板的温度梯度在-0.275～0.62℃/cm之间变化。

图4 实测轨道板表面和底面温度

图5 轨道板表面与底面温度差

1.3 轨道板变形观测

轨道板的翘曲变形随着轨道板温度梯度的变化而变化。通过试验测得，当轨道板表面处于升温时，板表面温度高于板底面温度，轨道板边缘产生向下的翘曲变形，但由于水泥沥青砂浆层属于高弹性模量材料，抗压缩变形能力强，所以轨道板产生向下的翘曲变形量不大;当轨道板表面处于降温时，板表面温度低于板底面温度，轨道板边缘产生向上的翘曲变形，由于水泥沥青砂浆层抗拉变形能力弱，轨道板产生的翘曲量在0.1～0.45 mm变化。

2 轨道板有限元模拟分析

2.1 建立模型

在使用有限元软件Ansys模拟计算时，依据轨道板的结构特性，选择合理的单元建立轨道板模型，模型如图6所示。钢轨、扣件、轨道板、水泥沥青砂浆层分别采用Beam单元、弹簧单元、实体单元、杆单元模拟;底座采用固定位移约束模拟。

图6 轨道板有限元模型

2.2 分析假设

依据实测轨道板表面和底面温度，温度差在-5.5～12.4℃，温度梯度-0.275～0.62℃/cm;在有限元模拟计算过程中，假设轨道板沿厚度方向的温度梯度呈线性分布。钢轨、扣件和轨道板的材料参数参照相关规范，水泥沥青砂浆为高弹性模量材料(受压不受拉)，弹性模量Eca=7 000～10 000 MPa。

2.3 模型参数确定

为了验证建立的有限元模型能够反映实际轨道板的温度变形，下面分别从轨道板升降温、水泥沥青砂浆弹性模量和钢轨、轨道板自重3个方面讨论，确定模型参数。

情况1，轨道板温度采用实测温度，考虑钢轨、轨道板自重，水泥沥青砂浆的弹性模量取值7 000～10 000 MPa，轨道板边角的翘曲变形量与水泥沥青砂浆的弹性的变化关系如图7所示。

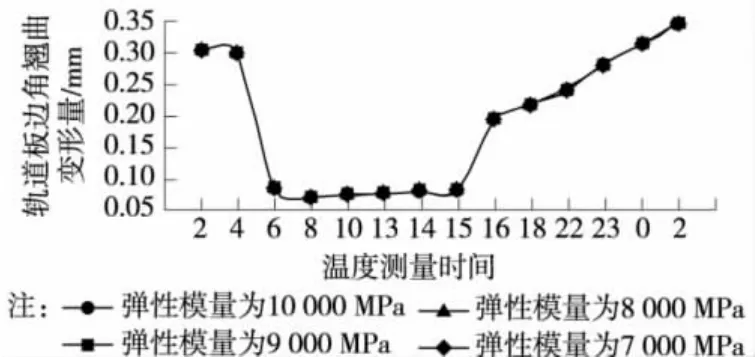
图7 轨道板翘曲变形量与水泥沥青砂浆弹性模量的关系(考虑钢轨、轨道板自重)

从模拟结果曲线可知，水泥沥青砂浆的弹性模量对轨道板的翘曲变形影响很小。

从2:00～6:00，轨道板底面温度大于表面温度，随着轨道板表面升温，表面温度逐渐升高，温度梯度增大，轨道板的翘曲变形量逐渐减小，轨道板的最大翘曲变形量为0.3 mm;

从6:00～15:00随着轨道板表面温度继续升高，轨道板表面温度大于底面温度，轨道板4个边角产生的翘曲变形量基本保持不变，约为0.08 mm;

从15:00～2:00，随着轨道板表面温度的降低，板底面温度大于板表面温度，轨道板4个边角产生向上的翘曲变形，最大翘曲变形量为0.35 mm。

图8显示在2:00，当水泥沥青砂浆的弹性模量为8 000 MPa时，轨道板的翘曲变形云图。最大的翘曲变形发生在轨道板4个边角位置，翘曲变形量为0.35 mm。

图8 轨道板翘曲变形云图

情况2，轨道板温度采用实测温度，忽略钢轨、轨道板自重，水泥沥青砂浆的弹性模量为8 000 MPa时，轨道板的翘曲变形量与水泥沥青砂浆的弹性的变化关系如图9所示。

图9 钢轨、轨道板自重对翘曲变形的影响

当轨道板底面温度大于表面温度时，忽略钢轨、轨道板自重，轨道板产生的翘曲变形量要比考虑自重产生的翘曲变形量大30%;当轨道板表面温度大于底面温度时，考虑自重和忽略自重，轨道板边角的翘曲变形量基本一致。

考虑自重轨道板产生的最大翘曲变形量为0.35 mm;忽略自重轨道板产生的最大翘曲变形量为0.473 mm;通过与试验测量的最大翘曲变形量0.45 mm相比，当模型参数忽略钢轨、轨道板自重、水泥沥青砂浆的弹性模量为8 000 MPa时，数值模拟计算结果与实际测量结果基本一致。

3 轨道板模型的应用

由于CRTSⅡ型板无砟轨道采用纵联结构，前面对单一轨道由于温度梯度变化产生的翘曲变形进行了分析，下面基于单一轨道板模型，建立3块纵联轨道板模型，分析轨道板纵联后温度梯度对轨道板翘曲变形的影响。

3块纵联轨道板有限元模型如图10所示。

图10 纵联轨道板分析模型

其中，水泥沥青砂浆的弹性模量取8 000 MPa，忽略钢轨、轨道板自重，温度梯度取-0.275℃/cm，轨道板的翘曲变形量取中间轨道板模拟结果。

从模拟结果可知，中间轨道板4个边角产生向上最大翘曲变形为0.33 mm。与前面单一轨道板最大翘曲变形量0.473 mm相比，纵联后轨道板翘曲变形量比单块轨道板的翘曲变形量减小约30%。

4 结论与展望

本文基于对CRTSⅡ型板无砟轨道温度和变形的测量，使用Ansys有限元软件建立分析模型，分析不均匀温度梯度对轨道板翘曲变形的影响，通过试验测量数据和模拟结果的对比，确定模型参数并验证分析模型的可靠性，得到如下结论。

(1)依据实测轨道板温度数据，可知轨道板板底与表面的温度随日照、时间的变化而变化，板表面与底面温差变化幅度为-5.5～12.4℃，温度梯度在-0.275～0.62℃/cm变化;

(2)通过试验测量数据和模拟结果的对比，验证当轨道板板底温度高、板表面温度低时，轨道板4个边角产生向上翘曲变形;水泥沥青砂浆的弹性模量对轨道板的翘曲变形影响很小;当忽略钢轨、轨道板自重时，数值模拟计算结果与实际测量结果基本一致。

(3)依据单一轨道板模型以及模拟参数，建立3块纵联轨道板模型，纵联后轨道板由温度梯度产生的翘曲变形量比单块轨道板的翘曲变形量减小约30%。

本次对轨道板温度测量是在8月份进行，缺少其他季节测量数据，需要进一步完善。待数据完善后，需要进一步验证分析模型的可靠性。

［1］王其昌，韩启孟.板式轨道设计与施工［M］.成都:西南交通大学出版社，2002.

［2］龚曙光，谢桂兰.ANSYS操作命令与参数化编程［M］.北京:机械工业出版社，2004.

［3］王森荣，孙 立，李秋义.无砟轨道轨道板温度测量与温度应力分析［J］.铁道工程学报，2009(2).