FDT-2型柔性轨道形变参数计算与分析
阚 颖,谢新连,蔡 琦
(大连海事大学交通运输管理学院,大连 116026)
为提高火车渡轮的装载量和装卸效率,增强火车渡轮引桥对船型的适应性,文献[1~4]中提出了一种以短轨构成,并在短轨之间预留一定伸缩间隙的新型柔性连接轨道(Flexible Double-rail Track),简称为FDT-1型柔性连接轨道。在FDT-1型柔性连接轨道的基础上,本文提出一种轨枕与钢轨刚性连接成一体,在轨枕两端设有推拉机构,通过轨枕中部互相铰接而形成的轨道,简称为FDT-2型柔性连接轨道,见图1。在推拉机构的作用下,轨枕以中间连接销轴为圆心微量旋转,一端的轨枕间隙减小,另一端的轨枕间隙增大,即同一侧的轨枕端部,或同时靠近或同时疏远。通过这种方式使得轨道曲率产生变化,进而实现整条轨道的柔性。
本文给出FDT-2型柔性轨道弯曲变形过程中主要形变参数的表达式,通过数值分析与计算,直观表达FDT-2型柔性轨道的主要弯曲变形参数与设计参数之间的函数关系,说明改型柔性轨道的可行性和设计原理,进而得出其主要设计参数的参考值。
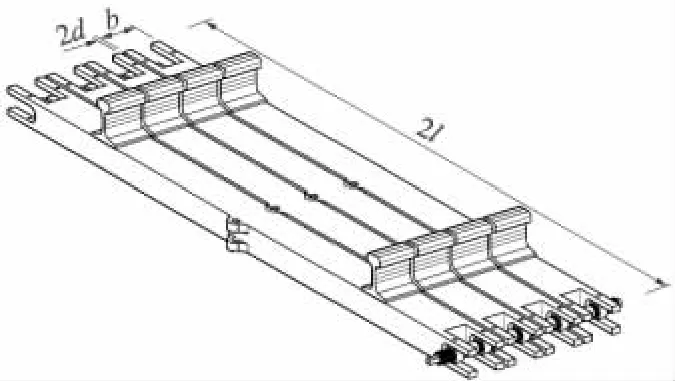
图1 FDT-2型柔性轨道俯视图
1 问题描述与假设
根据文献[1],在装卸火车渡轮过程中,岸上的轨道与船甲板上的轨道主要有3种连接情况。一是岸上的固定轨道与甲板上的固定轨道平行,且在同一条直线上;二是岸上的固定轨道与甲板上的固定轨道不平行,也不在同一条直线上;三是岸上的固定轨道与甲板上的固定轨道平行,但不在同一条直线上。第一种情况比较简单,岸上的固定轨道与甲板上的固定轨道可以用直线式轨道直接连接。第二种情况下,连接轨道的曲线形状也比较简单,一般为单向曲线。第三种情况下,要求连接船、岸上两段固定轨道的柔性轨道要由两段反向曲线组成。本文主要讨论船、岸轨道第三种连接情况下柔性轨道的形变参数问题。
以轨道的中心线表达轨道弯曲的形状,设第三种情况中柔性连接轨道(中心线)由两段反曲的圆弧组成,两段圆弧的中点为两段圆弧组成的轨道曲线的反曲点。在固定轨道与柔性轨道的连接点和轨道曲线的反曲点处两段轨道相切(暂不考虑轨道的曲率过渡问题),也即整个柔性轨道形状是关于其中心线上反曲点的中心对称图形。为建立柔性轨道的弯曲变形参数与其设计参数的关系,按照图2所示,建立X-Y坐标系,将柔性轨道置于坐标系内。X方向为轨枕长度或轨道横方向,Y方向为轨道延伸方向。设x=0,y=0为坐标原点,y=0,即X轴为柔性轨道与陆上固定轨道的连接处。
设柔性轨道接陆端第1根轨枕编号为0,由此向柔性轨道的自由端(接船端)对轨枕顺次编号,i=0,1,2,……,2n+1。从轨枕1开始,各轨枕在推拉机构的作用下会产生偏移。又设轨枕长度为2l;轨枕宽度为b;沿轨道长度,相邻轨枕之间的设计间隙均为2d;轨距为2g。其他符号意义如下:
α——轨枕相对偏转角,表示第i+1个轨枕相对于第i个轨枕的偏转角,设轨道在弯曲过程中,所有相邻轨枕的相对偏转角相等;
αi——第i个轨枕的偏转角,表示第i个轨枕相对于编号为0(即固定端)的轨枕的偏转角;
αmax——轨枕最大相对偏转角,表示轨枕相对偏转角的最大值,受相邻轨枕之间设计间隙大小的影响;
R——柔性轨道弯曲后的曲率半径;
ΔxB,i、ΔyB,i——分别表示柔性轨道上第 i根轨枕靠船侧中点在X轴方向的偏移量和在Y轴方向的偏移量;
δy、δs——分别表示柔性轨道弯曲后,轨道中心线内侧(间隙减小一侧)相邻钢轨之间的间隙和轨道中心线外侧(间隙增大一侧)相邻钢轨之间的间隙。
在FDT-2型柔性轨道的这些参数中,柔性轨道长度2L、轨枕长度2l、轨枕宽度b、相邻轨枕之间的间隙2d、轨距2g等为设计参数,因为这些参数要在设计柔性轨道时确定。柔性轨道使用中,弯曲后的曲率半径R、相邻钢轨之间的间隙δy和δs、相对偏转角α、自由端轨枕靠船侧中点在X轴方向的偏移量ΔxB,i和在Y轴方向的偏移量ΔyB,i等为形变参数,在使用柔性轨道时这些参数是变化的。形变参数的变化范围取决于设计参数,同时又决定了柔性轨道的性能。
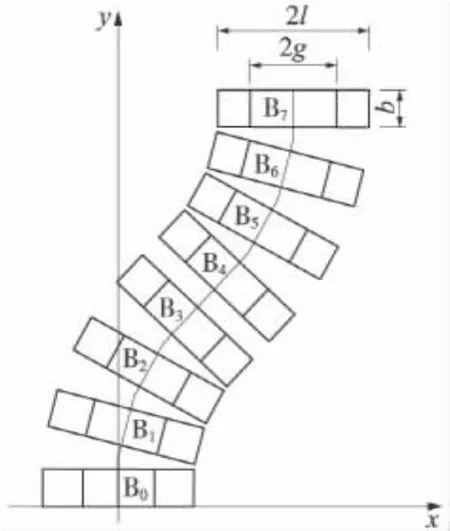
图2 轨道整体偏移情况示意
2 柔性轨道形变参数表达式推导
为便于推导及叙述,先将柔性轨道从反曲点处分为两部分,以其中一部分(即与固定端相连接的半边)为例进行柔性轨道形状参数表达式的推导。根据前文假设,柔性轨道半边包含的轨枕数目为n+1。柔性轨道半边弯曲后形成的偏转角度为αn,即柔性轨道(半长)两端轨向差。当控制任意两个相邻轨枕的相对偏转角均为α时,可得推导出如下算式。

当柔性轨道达到最大弯曲程度,即间隙减小一侧相邻轨枕端部接触时,相对偏转角α最大,达到αmax。此时有
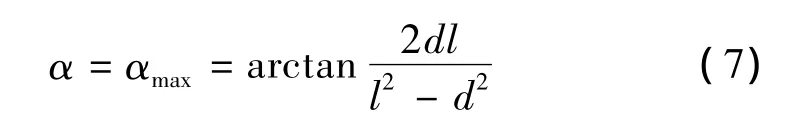
基于上述公式,可以进一步求出由两段反曲圆弧构成的整段柔性轨道的形状参数。这里注意到,整段柔性轨道含有的轨枕总数为2(n+1)。因此,如果将柔性轨道接陆端第一根轨枕的编号设为0,则向自由端或接船端柔性轨道中各轨枕编号顺次为,i=0,1,2,…,2n+1。
研究柔性轨道在第三种连接情况下整体弯曲特性时,需要补充计算出柔性轨道总的偏转角或转向角、柔性轨道自由端或接船端的X、Y方向移动量等重要参数。其中柔性轨道总的偏转角及轨道弯曲后的曲率半径仍然可用式(1)、(2)求得。而柔性轨道自由端或接船端的移动量就是第2n+1号轨枕的位移量。第2n+1号轨枕的位移量可以用B2n+1点的位移量表达,见图2。
设轨道处于平直状态时,B2n+1点的坐标为(0,y2n+1),弯曲偏移后 B2n+1点的坐标为(xB,2n+1,yB,2n+1)。则 B2n+1在 X 轴的偏移量 ΔxB,2n+1=xB,2n+1-0,在 Y 轴的偏移量 ΔyB,2n+1=yB,2n+1-y2n+1。因 y2n+1=(2n+1)(b+2d)+b,所以

由于假设轨道在弯曲过程中,所有相邻轨枕的相对偏转角相等,因此轨道弯曲时,同一曲向、同一侧的短钢轨之间间隙相等,内侧和外侧钢轨线上短钢轨之间间隙仍然可以用公式(5)、(6)分别计算。
3 数值计算与分析
根据上节推导出的柔性轨道形变参数表达式,对柔性轨道主要设计参数和形变参数进行数值分析,以便直观观察柔性轨道主要设计参数和形变参数的合理变化范围。根据对现有铁路渡轮系统中相关数据的测算及对相关参数的合理估计[5],设定柔性轨道各设计参数的一组初始值。设相邻轨枕间距的一半d=7.5 mm,轨枕宽度b=145 mm,n=300,即整段柔性轨道中包含的轨枕总数为602根时,轨道整体长度2L为96.305 m。又设轨枕长度的一半l=1 300 mm,轨距的一半g=725 mm。以此组设计参数作为分析的基础,同时应考虑如下几点影响因素:
第一,设渡轮装载甲板上至少设置7条轨道,相邻轨道中心线间距4 m,即 ΔxB,2n+1的最大值应不小于12 m。
第二,当柔性轨道产生偏移时,在Y轴方向必然出现一个缩短量,即 ΔyB,2n+1。ΔyB,2n+1取值不宜过大,否则,对预先制作的标准延伸接头的要求将会提高。
第三,定义相邻轨枕的钢轨间隙 δmax=max(δy,δs)。根据 δy,δs的定义,δmax=δs为避免车辆运行的颠簸和不平稳,δmax不宜过大。
第四,考虑到行车安全问题,轨道曲率半径R不宜过小。
第五,在满足设计及安全性要求的前提下,轨道整体长度2L应尽可能地小。
(1)形变参数值随轨枕宽度b值变化而变化的分析
改变设计参数 b,令轨枕宽度 b=115,130,145,160,175 mm,计算相关的形变参数值。取相对偏转角α为基本形变参数,在上述一组设计参数下,不难算出轨枕最大偏转角αmax=0.661°。定义单位长角变量为αn/L,单位长横移量为ΔxB,2n+1/2L,令相对偏转角 α=0.040°,0.052°,0.063°,计算结果列于表 1。

表1 b值变化的形变参数值计算
观察表1中的数据可知,当轨枕宽度b值变化时,同一相对偏转角 α对应的曲率半径 R、ΔxB,2n+1、ΔyB,2n+1发生改变,其绝对值随b值的增加而增加,同一相对偏转角α对应的单位长角变量随b值的增加而减小,同一相对偏转角α对应的单位长横移量及相邻轨枕的钢轨间隙δmax不变;当相对偏转角α发生变化时,同一 b 值对应的单位长角变量、ΔxB,2n+1、ΔyB,2n+1、单位长横移量及相邻轨枕的钢轨间隙δmax发生改变,其绝对值随偏转角的增加而增加,同一b值对应的曲率半径R随偏转角α的增加而减小。即曲率半径R、单位长角变量、ΔxB,2n+1、ΔyB,2n+1的变化与 b 值和相对偏转角α有关,单位长横移量、相邻轨枕的钢轨间隙δmax与b值无关,只与相对偏转角α有关。
(2)形变参数值随轨枕间隙2d值变化而变化的分析
设其他条件(设计参数)不变,改变相邻轨枕设计间距,令 d=3,4.5,6,7.5,9 mm,分别计算相关的形变参数值。同样取相对偏转角α为基本形变参数,令相对偏转角 α =0.040°,0.052°,0.063°,计算结果列于表2。
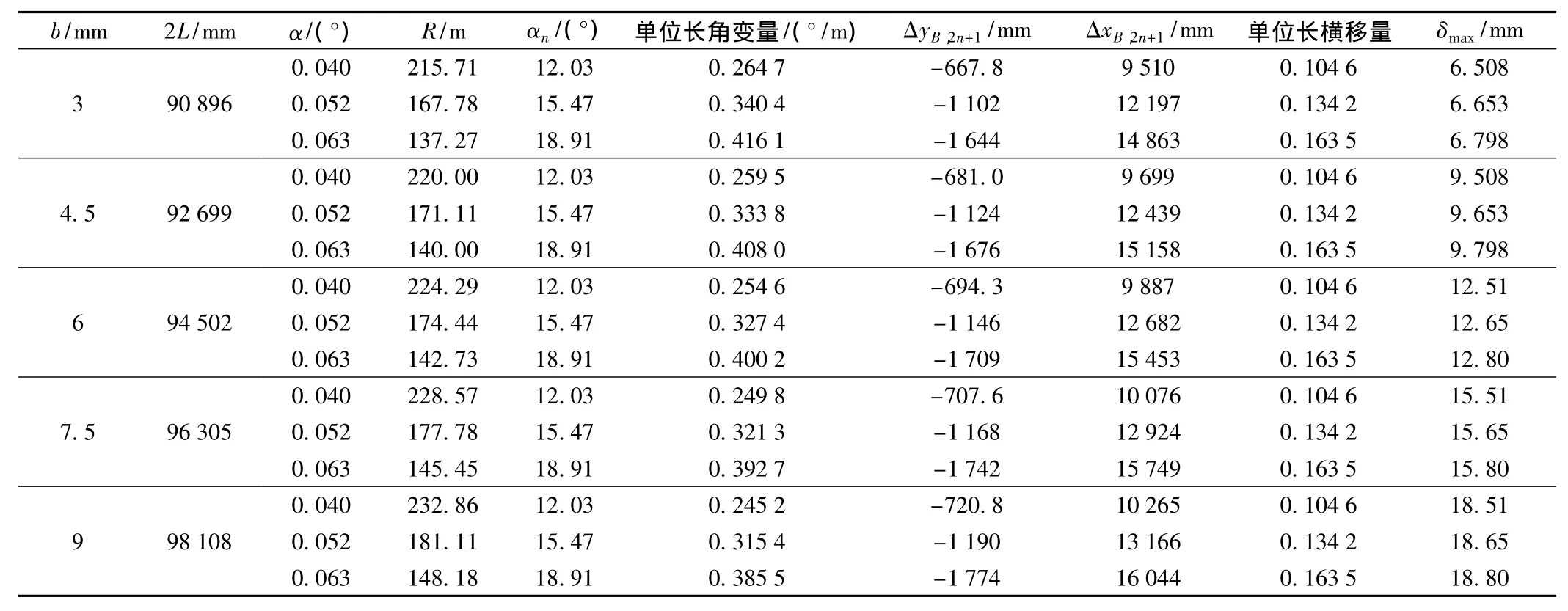
表2 d值变化的形变参数值计算
观察表2中的数据可知,当d值变化时,同一相对偏转角 α 对应的曲率半径 R、ΔxB,2n+1、ΔyB,2n+1及相邻轨枕的钢轨间隙δmax发生改变,其绝对值随d值的增加而增加,同一相对偏转角α对应的单位长角变量随d值的增加而减小,同一相对偏转角α对应的单位长横移量不变;当相对偏转角α发生变化时,同一d值对应的单位长角变量、ΔxB,2n+1、ΔyB,2n+1、单位长横移量及相邻轨枕的钢轨间隙δmax发生改变,其绝对值随偏转角α的增加而增加,同一d值对应的曲率半径R随偏转角α的增加而减小。即曲率半径R、单位长角变量、ΔxB,2n+1、ΔyB,2n+1和相邻轨枕的钢轨间隙 δmax的变化与d值和相对偏转角α都有关,单位长横移量与d值无关,只与相对偏转角α有关。
(3)限定偏转角度αn下要求的轨枕数量分析
对于本节开头设定的1组设计参数,分析当给定轨道转向角度αn时要求柔性轨道必须具有的轨枕数量。当相对偏转角 α=αmax和 α=0.052°<αmax时,由公式(1)、(7)可求得表3中数据。
相对偏转角α相同时,轨枕总数随轨道转向角αn的增加而增加;转向角αn相同时,相对偏转角α越小,对应的轨枕总数越大。表3中给出了轨枕总数与转向角关于α的两个典型值的理论计算结果,在实际应用中,转向角αn根据具体情况的不同会有一定的变化范围。
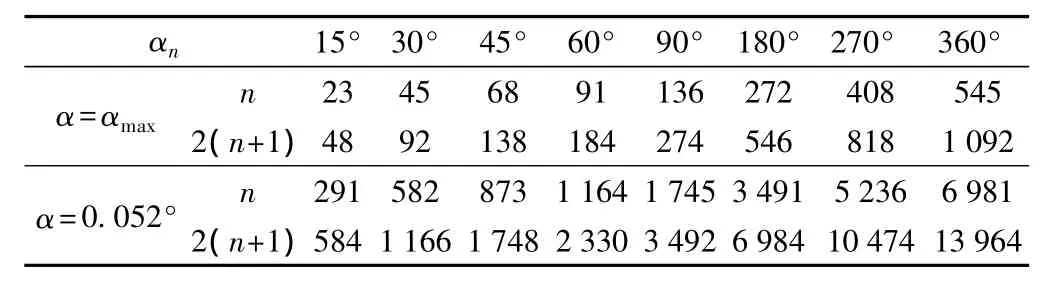
表3 轨枕总数随柔性轨道总的偏移角度变化而变化的情况
根据行车安全要求和上述理论分析和数值计算结果,认为柔性轨道的主要设计参数和形变参数的合理取值范围如表4所列。
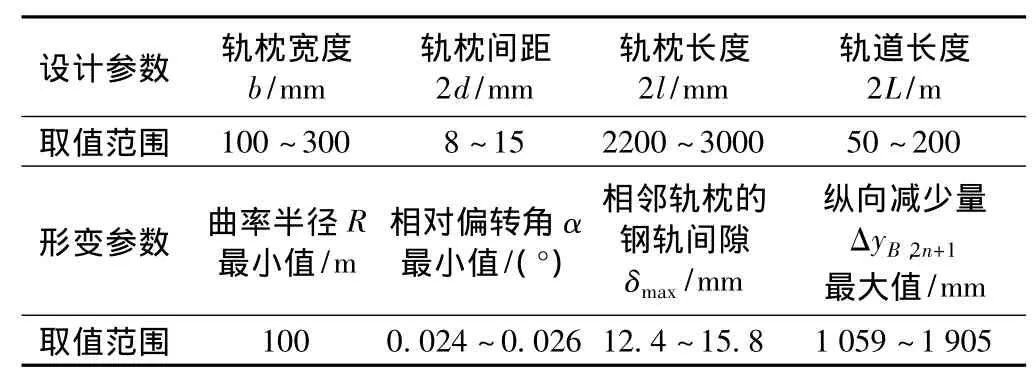
表4 柔性轨道主要参数的建议取值范围
表4中列出的建议参数值应根据具体问题和要求确定,不能随意设定。因各个参数之间具有内在的联系,必须在考虑其各自变化的规律性后经过优化确定。
4 结论
本文推导了FDT-2型柔性轨道主要形变参数与设计参数之间的函数关系,并系列改变设计参数,观察形变参数的变化规律,用于指导FDT-2型柔性轨道的设计和表明柔性轨道的工程可行、实用范围。主要研究结论如下:
(1)柔性轨道弯曲变形的性能与其轨枕宽度、相邻轨枕间距及轨枕总数或柔性轨道长度有关。本文给出的柔性轨道整体弯曲变形计算公式可以用于柔性轨道工程设计。
(2)定量分析了柔性轨道主要设计参数对形变参数的影响程度和影响规律,可供实际工程设计参考。
(3)通过数值计算与比较,给出了柔性轨道主要设计参数的建议取值范围。
[1]谢新连,张 量,王少成.新型铁路柔性轨道弯曲变形量计算[J].铁道学报,2003,25(4):31-34.
[2]谢新连,刘涛,王少成,等.火车渡轮柔性轨道受力变形计算[J].船舶力学,2007,11(1):88-93.
[3]Xie Xinlian.An Integrated Sea-land Transportation Systems Model and its Theory[J].Transportation Research Part C:Emerging Technologies,2009,17(4):394-411.
[4]Xie Xinlian,Li Meng,Liu Shiyong,et al.On the flexible connection of rigid double-railtrack[C]∥ Proceedingsofthe Second International Conference on Intelligent Computation Technology and Automation(ICICTA),Volume 04.Washington,DC,USA:IEEE Computer Society,2009:581-585.
[5]阚 颖,谢新连,赵家保.铁路渡轮装卸过程模拟方法初探[J].中国航海,2010,33(2):89-94.

