考虑泊松比的固体发动机装药贮存寿命预估①

职世君，孙 冰，张建伟

(北京航空航天大学宇航学院，北京 100191)

0 引言

固体火箭发动机的寿命预估一直是设计和使用部门特别关注的问题，固体发动机装药结构寿命是影响发动机寿命的重要因素，国内外对此展开了大量试验和理论研究。其中，利用加速老化试验法或长期贮存试验法确定推进剂的相关力学性能参数，再结合装药的结构完整性分析，对固体发动机装药结构寿命进行预估的方法［1－2］应用较广泛。由于在发动机的贮存过程中，固体推进剂发生了化学老化和物理老化，使得固体推进剂的力学性能发生了较大变化［3－5］。因此，在对发动机装药进行结构完整性分析时，固体推进剂老化参数的选取显得十分重要。因为发动机装药的有限元计算结果主要受推进剂的松弛模量和泊松比的影响。其中，泊松比的微小变化会对药柱内部危险部位的应力、应变产生较大影响［6－7］。所以，在考虑推进剂老化松弛模量变化的同时，不能忽略泊松比的影响，这样才更符合实际情况。

本文根据Wash理论及弹性力学公式，推导了固体推进剂初始泊松比与空穴率的关系，利用推进剂空穴率的贮存试验结果［8］，近似得到了初始泊松比的变化规律。根据加速老化法得到推进剂瞬时模量及最大延伸率的贮存变化规律，结合有限元计算方法，预估了常温贮存下发动机装药结构寿命。

1 推进剂泊松比与空穴率的关系

假设固体推进剂为各向同性材料，小孔隙在推进剂内均匀分布，从细观尺度上认为，推进剂由若干个含1个小孔隙的立方体组成，取其中1个立方体为代表性体积单元进行分析，单元的空穴率与推进剂相等，如图1所示。

图1 固体推进剂代表性体积单元Fig.1 Representative volume element of solid propellant

固体推进剂为时域相关性材料，在受载时，其松弛模量为随时间变化的函数。当t=0时，即推进剂受载的瞬间，可将推进剂作为弹性体求解。由于推进剂空穴率较小，所以不考虑孔隙间的相互影响和小孔隙内部压强，为求解小孔附近的径向位移，可把问题简化为壁厚很大的空心球(a≪b)。当代表性体积单元受压力载荷时，则孔隙附近瞬时径向位移为

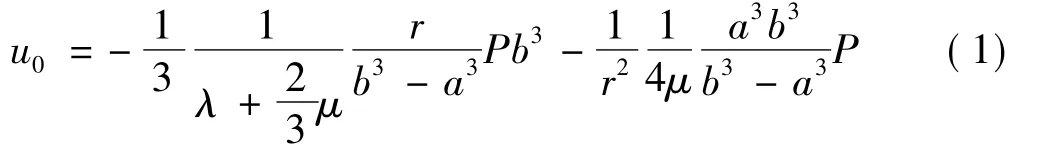
式中 λ和μ为拉梅常数。

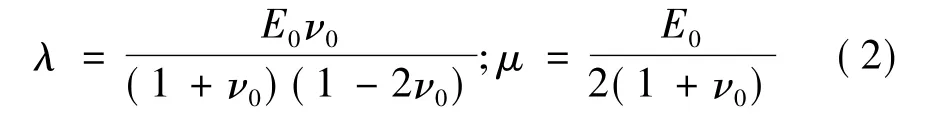
式中 E0为瞬时模量;ν0为瞬时泊松比。

由 a≪b，可得

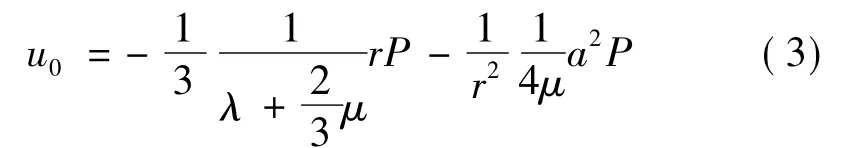
令r=a，可得孔隙半径的变化Δa为

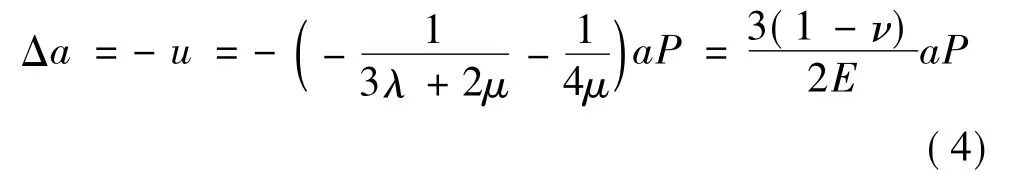
孔隙体积的变化ΔV'为

将式(4)代入式(5)，可得

则

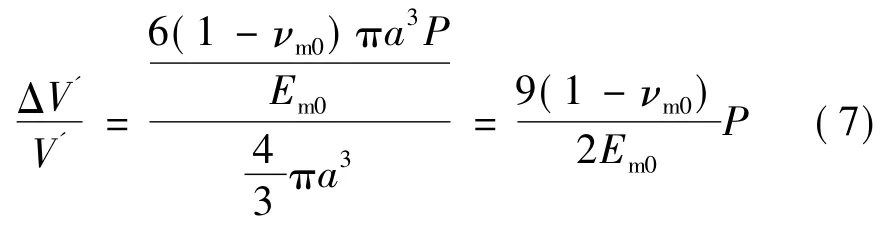
式中 Em、νm分别为推进剂基质的瞬时模量和瞬时泊松比。

根据 Wash 公式［9］:

式中 βeff为推进剂的等效压缩系数;βm为推进剂基质的压缩系数。

式中 K为体积模量;E为弹性模量;ν为泊松比。

则式(8)可转化为

即

在对发动机进行结构仿真时，固体推进剂采用的是线性积分本构方程。固体推进剂粘弹泊松比是随时间变化的函数，从初始值随时间逐渐增长，最后达到接近0.5的平衡值［7］。假设固体推进剂的瞬时体积模量主要受空穴率的影响，即认为推进剂基质参数Km0和νm0为常数，根据固体推进剂的瞬时泊松比公式:

将式(12)代入式(13)，可得泊松比与空穴率的关系式:

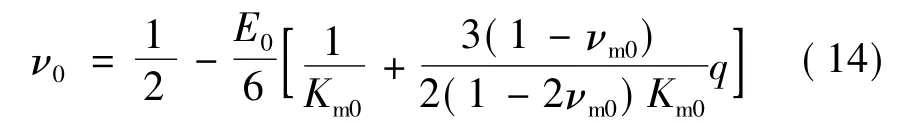
为近似反映固体推进剂泊松比随老化时间的变化规律，空穴率采用文献［8］中老化试验数值，由于推进剂为近似不可压缩材料，未老化时泊松比较大，因此近似取此时的泊松比为固体推进剂基质泊松比，即νm0=0.499。固体推进剂泊松比随老化年限的变化规律如图2所示。从图2中可看出，随固体推进剂老化年限的增加，泊松比逐渐下降，且下降速率逐渐增加。这与固体推进剂在贮存过程中空穴率不断增加，且增长速率逐渐增大是对应的。

2 加速老化试验数据处理

根据航天工业标准QJ 2328A—2005，用于数据处理的3个老化数学模型分别为

式中 P为固体推进剂某一老化时刻的性能参数;P0为初始性能参数;K为与温度相关的性能变化速率;t为老化时间。

图2 固体推进剂泊松比随老化时间的变化曲线Fig.2 Variation of Poisson＇s ratio vs aging time

在固体发动机的贮存过程中，药柱的老化主要是由于粘结剂的氧化交联及降解断链影响，从整体来看，由于粘结剂的氧化交联作用在推进剂贮存过程中占主导地位，因此固体推进剂随贮存时间逐渐变硬，导致了固体推进剂最大延伸率的下降及松弛模量的增加。

2.1 最大延伸率

根据最大延伸率的试验数据分布，采用式(17)对试验数据进行处理，结合Arrhenius公式:

可得

对试验数据进行拟合，可得

式中 A为表观频率因子;Ea为表观活化能;R为玻尔兹曼常数。

2.2 松弛模量

在有限元计算时，推进剂松弛模量是以Prony级数给出:

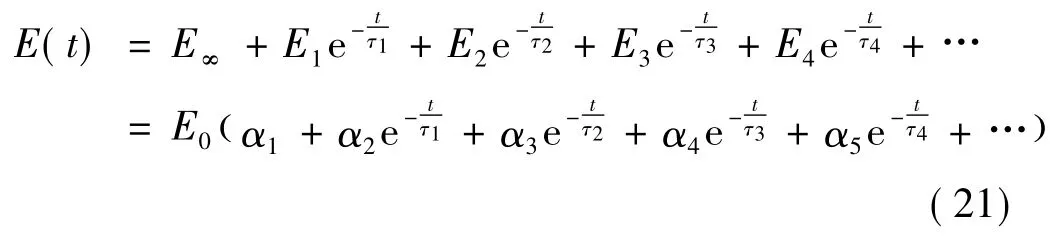
式中 E0为推进剂的瞬时模量;E∞为平衡模量;α1=

由于Prony级数的表征参数较多，拟合Prony级数往往需大量的松弛试验，若拟合不同贮存时间的推进剂Prony级数，则试验成本很高。假设推进剂随时间的松弛特征参数，即式(21)中的αi及τi基本不变，以E0的变化来反映固体推进剂老化时Prony级数的变化规律。E0的老化数学模型选用式(16)，结合Arrhenius公式，可得

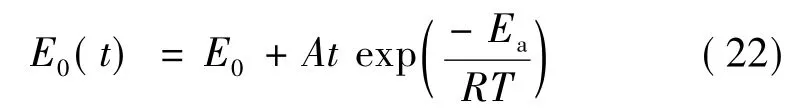
对试验数据进行拟合，可得

结合未贮存时推进剂的Prony级数:

则可知，在贮存温度为25°C时，不同贮存年限的推进剂Prony级数曲线如图3所示。

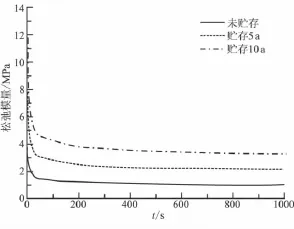
图3 不同贮存时间推进剂Prony级数曲线Fig.3 Prony series of propellant with different storage time

3 有限元计算及结果分析

3.1 有限元计算模型

某发动机主要由金属壳体、绝热层和推进剂组成。药柱为六角星形，根据对称性取发动机1/12建模，采用六面体单元对发动机模型进行网格划分。其中，发动机药柱网格模型如图4所示。

在计算中，主要考虑了发动机所经历的3个载荷工况:固化降温、弹射和点火发射。其中，固化降温时，药柱经历40 h，从零应力温度60°C降到20°C。然后，在25°C环境下贮存并发射，该发动机采用保温弹射方式进行发射。弹射时，发动机尾部发射筒与尾罩之间瞬间产生高压气体，使发动机产生约10 gn的加速度载荷。点火时，发动机受内压载荷作用，压力峰值为6 MPa，由于发动机推力作用，发动机同时受约5 gn的轴向加速度载荷。

图4 某固体发动机药柱三维有限元模型Fig.4 Three dimension finite element model of a SRM grain

3.2 计算结果分析

分别对未贮存至贮存15 a间不同贮存年限的发动机进行三维粘弹性有限元计算。在固化降温过程，采用发动机出厂的材料参数;在弹射过程及发动机点火过程，采用相应贮存年限的材料老化参数。

图5是有限元模拟发动机贮存0、5、10、15 a后在点火发射工况下发动机的等效应变分布。由图5可见，在发动机贮存过程中，药柱的老化对发动机等效应变的分布规律影响不大，装药的危险点位于发动机前封头附近，即图中A点处。统计算例中不同贮存年限发动机危险点的最大Von-Mises等效应变。由于推进剂的泊松比接近 0.5，可认为 εVon与 εm近似相等［1］，将装药最大等效应变随贮存时间的变化曲线与最大延伸率的变化曲线进行对比，如图6所示。另外，为对比考虑泊松比变化与未考虑泊松比变化的计算结果，将发动机药柱老化过程中泊松比设为定值，对发动机进行了有限元计算。

图5 不同贮存年限发动机等效应变Fig.5 Von-Mises strain of SRM with different storage time

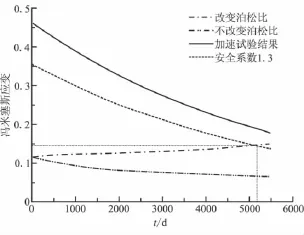
图6 常温贮存下发动机装药寿命预估Fig.6 Storage life prediction for SRM in normal temperature

从图6可看出，考虑推进剂老化泊松比变化时，装药危险点的最大等效应变随贮存时间的增加而增加，未贮存时为11.68%，贮存15 a后变为14.92%。未考虑泊松比变化时，装药危险点的最大等效应变随贮存时间的增加而减小，贮存15 a后变为6.59%。可见，固体推进剂泊松比在贮存过程中虽然只发生了微小变化，但对计算结果影响较大，考虑与未考虑泊松比变化时的计算结果有明显差异。

由于制造技术、贮存环境载荷及推进剂细微颗粒分布的随机性，推进剂的最大延伸率、松弛模量等特征参数有一定的不确定性，且随贮存年限的增加，离散性越来越大［10］。因此，在预估装药结构寿命时，需取一定的安全系数，本文取安全系数为1.3，结合图6可知，发动机装药结构寿命为14.2 a。

4 结论

(1)分析推导了固体推进剂小孔隙空穴率与初始泊松比的关系，得到了固体推进剂泊松比随贮存时间的变化规律，即固体推进剂初始泊松比随贮存时间的增长而逐渐减小。在发动机的结构完整性分析中，考虑了泊松比随推进剂老化的变化，更符合实际情况。

(2)根据加速老化试验数据及航天工业标准，得到了推进剂最大延伸率和瞬时模量随贮存时间的变化规律。由于固体推进剂粘结剂的氧化交联作用，使得推进剂在贮存过程中，其最大延伸率逐渐下降，松弛模量逐渐增大。

(3)在推进剂瞬时模量和瞬时泊松比的综合作用下，装药危险点的最大等效应变随贮存年限的增加而增大，而未考虑泊松比的最大等效应变呈逐年下降趋势。考虑与未考虑泊松比变化的计算结果存在明显差异。取安全系数为1.3时，该发动机装药的贮存寿命为 14.2 a。

［1］袁端才，唐国金，李海阳，等.基于加速老化与三维粘弹性有限元分析的固体导弹发动机寿命预估［J］.兵工学报，2006，27(4):685-689.

［2］邢耀国，马银民，董可海.用长期贮存定期检测法预测药柱使用寿命［J］.推进技术，1999，20(5):39-43.

［3］Christiansen A G，Layton L H and Carpenter R L.HTPB propellant aging［J］.J.Spacecraft，1981，18(3):211-215.

［4］Kivity M，Hartman G，Achlama A M.Aging of HTPB propellant［R］.AIAA 2005-3802.

［5］Gary L.Solid propellant aging kinetics［R］.AIAA 2009-5423.

［6］赵伯华.固体推进剂粘弹泊松比的研究［J］.北京理工大学学报，1994，14(1):87-90.

［7］郝松林.高填充复合推进剂的初始粘弹泊松比［J］.固体火箭技术，1996，19(4):46-50.

［8］沈庭芳，赵伯华.固体推进剂空穴损伤的理论与实验分析［J］.推进技术，2002，23(1):71-73.

［9］陈颙，黄庭芳.岩石物理学［M］.北京:北京大学出版社，2001.

［10］高鸣，徐廷学.固体火箭发动机药柱可靠性及寿命预估研究［J］.固体火箭技术，2008，31(3):220-240.