轴向均布荷载压杆稳定问题的重心插值配点法

于卫涛，宋洁，赵维霞

(1.滨州市建设工程质量监督站，山东 滨州 256600;2.滨州市工程建设标准定额站，山东 滨州 256600;3.山东城市建设职业学院，山东 济南 250014)

0 引言

当等直杆件受均布轴向荷载作用时，采用静力平衡准则判断原始直线状态的平衡稳定性，首先应给予杆件微小偏移，使之呈现弯曲状态，看其杆件是否能平衡。如果存在平衡状态，则其处在平衡路径上的分岔点，也就是临界状态。此时的荷载即为临界荷载。至于临界状态以后的情况，若只采用线性理论则不能给出合理的说明。对于细长压杆，当载荷超过临界值时，压力与弯曲变形还存在一定的关系，这就是压杆的后屈曲性质。细长杆的后屈曲属于几何非线性问题。

在工程应用中，轴向均布荷载下压杆稳定问题可以归结为微分方程的边值问题，很难得到问题的解析解，一般采用数值方法求解。数值求解方法主要有有限差分法和有限元方法[1]等，这两种方法要对求解区域划分单元，计算精度依赖于单元的大小。采用配点法求解边值问题不需要划分单元，公式简单，不需要积分，易于编程。目前用于求解工程中的常微分方程边值问题的配点法主要有拟谱法和微分求积法。拟谱法[2－3]是根据谱方法发展出来的一种方法，虽然这种方法的理论研究已经有进一步的发展，但是工程技术人员对这种方法不是很了解。微分求积法[4－5]的基本原理是将未知函数在区间上所有离散点的函数值的加权和来逼近该函数在某一离散点的偏导数或者积分，这种方法中的权系数的确定通常是根据Lagrange多项式在网点处的导数值给出。但是这种方法的局限性是离散点不能取得太多，否则Lagrange多项式表示的曲线随多项式次数的升高而出现Runge现象，从而产生计算的不稳定性[6]。重心 Lagrange插值具有极好的数值稳定性[6]和极高的近似精度[7]，同时重心 Lagrange 插值公式具有紧凑的各阶导数的计算公式[8]。

本文所采用的重心插值配点法就是用重心Lagrange插值多项式求出某一函数在各个离散点的微分矩阵，从而可以通过矩阵的运算来求出微分方程的解。而许多结构力学问题的求解最终也归结为在一定的边界条件和初始条件下的(偏)微分方程(组)的求解，所以，可以把重心插值配点法作为用于结构力学问题的求解的一种数值方法。本文采用重心插值配点法求得了压杆屈曲的后屈曲挠度数值和屈曲路径分岔点的临界载荷值，精度较高，得到了满意的效果。

1 基于重心插值的微分矩阵

设g(x)为一待求函数，它在区间[0，L]上连续可微，现沿x轴设置N+1个节点，并以节点函数值g(xi)(j=0，1，…，N)作为基本未知量，且令 g(xj)=vj。在全域内采用重心Lagrange插值逼近g(x)，则有:

其中:mj为重心权。

因为所求解的问题是线性的，因此可以定义一个(N+1)×(N+1)的矩阵D。则(3)式可以写成如下的形式:

式中:w为未知函数一阶导数值构成的列向量;v为节点函数值的列向量;D就是对g(x)求一次导数的微分矩阵。由(1)、(2)、(3)式可得

2 轴向均布压力下细长压杆的重心插值配点法

细长杆在坐标原点处固定，顶端自由(图1)，杆件受到轴向均布荷载作用。s为以自由端为起始点沿杆方向的任意长度，θ为与过杆上一点的切线与与垂直线所成的角度，h为杆自由端x向位移，δ为杆自由端向位移。从载荷施加的初期到屈曲产生这一段时间杆件是维持竖直的，在临界载荷处发生分岔，屈曲产生之后，杆件发生变形挠曲，求解屈曲路径为大挠度问题。

假定杆件的材料是理想弹性，其应力应变关系符合胡克定律，变形和位移只要由弯曲产生，即略去剪切变形以及轴线的伸缩变形，杆的长度保持不变，并且假定横截面保持为平面。

图1 受轴向均布荷载细长压杆屈曲图

由文献[9]知，大挠度下压杆的变形方程无量纲化后为:

当压杆受轴向力作用时，到发生屈曲之前都是保持直线状态的，所以，在分岔点的研究上，可以近似的认为 sinθ≈θ，即:

杆件的变形方程为

式中:θ为N+1的转角位移参数列阵;D2是N+1行N+1列的2阶微分矩阵。

令 K=D2，Q=s×IN+1，则上式可以写成

其中:IN+1，为N+1行N+1列的单位阵。

则边界约束条件可以表示为:

将此2个方程的左边分别取代矩阵K的第1，N+1行，并把矩阵K和Q第N+1行放到矩阵的第1行和第2行之间，则原矩阵的第2行，第3行，…，第N行依次成为第3行，第4行，…，第N+1行。同样，把第N+1列放到矩阵的第1列和第2列之间，则原矩阵的第2列，第3列，…，第N列依次成为第3列，第4列，…，第N+1列。则K和Q变为:

用Matlab命令求矩阵Q－1K的特征值和特征向量就可得到屈曲临界值。一般的矩阵Q－1K的特征值有多个，将这些特征值按升序的方法排列，从中取出前几个特征值以及与它们相对应的特征向量。

微分矩阵以及梁的屈曲临界值和屈曲模态的计算，本文都编制Matlab程序来实现。解得k值与文献[9]对比如表1。

表1 不同取点对应的值

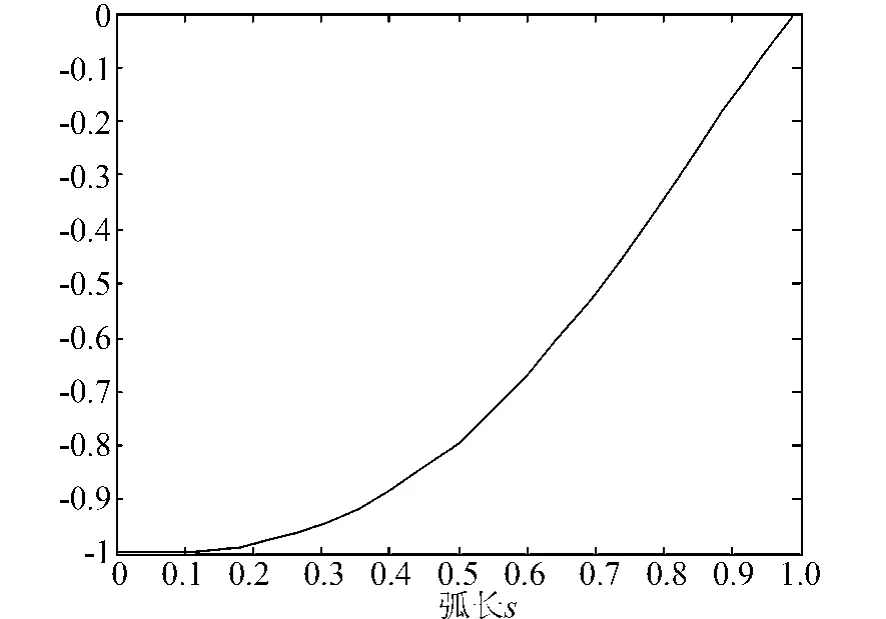
图2 一阶屈曲模态

可以看出，重心插值配点法比微分求积法收敛更快，且精度较高。

3 结论

对于屈曲临界值的求解，文献[10]用了多种方法，其中能量法应用的讨论非常详细，当取挠曲线方程为y=fsin[πx/(2l)]时，得出临界值为8.27;当取挠曲线方程为y=f(1－cos[πx/(2l)])时，得出的临界值为7.888;当取挠曲线方程为y=f1(1－cos[πx/(2l)])+f3(1 －cos[πx/(2l)])时，得出的临界值为7.84。即当选取的挠曲线月接近实际挠曲形状，得出的结果越精确。本文献中用静力平衡法得出的解为7.837，文献[11]由线性理论求解得出的临界值为7.837，文献[12]得出的临界值为7.83，本文也得出屈曲的临界值，解的前四位有效数值为7.837，与参考文献完全吻合，结果是可信的。

重心插值配点法是一种快速求解偏微分方程的方法。从算例可以看出，这种方法的精度很高。有限差分法和有限元法需要对求解区域划分单元，求解的精度取决于划分单元的大小，从而导致大的计算量。微分求积法的插值点不能取得太多，否则会出现插值数值不稳定性。本文采用的重心插值配点法不但可以避免上述方法的缺陷，而且可得到相当的精度。

[1]王勖成，邵敏.有限单元法基本原理及数值方法[M].2版，北京:清华大学出版社，2000.

[2]杨继明.热传导方程初边值问题的谱方法[J].湖南工程学院学报，2007，17(2):71 －73.

[3]聂国隽，仲政.微分求积单元法在结构工程中的应用[J].力学季刊，2005，26(3):423 －427.

[4]王维兰.拟lagrange多项式[J].西北民族学院学报:自然科学版，1999，20(4):15 －23.

[5]王兆清，李淑萍，唐炳涛.任意连续函数的多项式插值逼近[J].山东建筑大学学报，2007，22(2):158 －162.

[6]SCHNEIDER C，WERNER W.Some new aspects of rational interpolation[J].Math Comp，1986，47(175):285 －299.

[7]聂毓琴，孟广伟.材料力学[M].北京:机械工业出版社，2004.

[8]SHU C，DU H.Implementation of clamped and simply supported doundary conditions in the GDQ free vibration analysis of beams and plates[J].Int J Solids Structures，1997，34(7):819 －835.

[9]刘洋，杨永波，梁枢平.轴向均布载荷下压杆稳定问题的DQ解[J].力学与实践，2005，27(2):44 －47.

[10]吴明德.弹性杆件稳定理论[M].北京:高等教育出版社，1988.

[11]HOLDEN J T.On the finite defledtions of thin beams[J].Int J Solids Stuctures，1972(8):1051 －1055.

[12]TIMOSHENKO S P，GERE J M.Thery of elastic stability[M].MCGraw-Hill，1961.