基于模糊奇异摄动模型的直接型自适应控制器的设计

李 莉， 孙富春， 裴卫东

(1.天津师范大学计算机与信息工程学院，天津 300387;2.清华大学计算机科学与技术系人工智能重点实验室，北京 100084)

0 引言

由于存在强的柔性模态，带挠性附件航天器可以用含小摄动参数的多时标非线性系统进行描述。由于多时标系统中病态问题的存在，对其建模与控制比较困难。以往的处理方法通常是忽略较小的时间常数，对近似模型进行分析和综合［1－4］。这种方法实际上是仅对系统中呈慢变化部分的状态变量保留了小参数的零阶近似，而对系统中呈快变化部分的状态变量，不仅忽略了其小参数的高阶近似，也使得它在边界层内的值丢失了主要项，达到失真的程度。采用这种方法设计控制器，虽然能够降低控制器的阶次和简化其结构，但是往往不能满足系统的性能要求，甚至会导致闭环系统不稳定。

由于奇异摄动理论能够描述带有小参数的高阶微分方程，从20世纪60年代末到70年代初开始，用奇异摄动理论来研究、讨论多时标系统的分析和综合问题成为这一领域的主要方法并逐渐发展成熟。但是现有的控制策略都需要奇异摄动系统的模型已知，而且多用于线性系统，这在工业领域有时候很难达到。既然智能控制理论如模糊集和神经网络理论已经成功用于许多具有不确定性和建模误差的实际系统［5－6］，它们同样可以用于模型部分或全部未知的奇异摄动系统控制中。

孙富春及其课题组最早提出了一种模糊奇异摄动模型并在此领域开展了一系列研究工作［7－9］。在给出模糊奇异摄动模型的定义的基础上，进行了当摄动参数足够小时的闭环稳定性分析，并提出了镇定并行分布式补偿控制器，对连续或离散系统，其控制器增益可以分别归结为一组LMI或BMI，后者可以利用迭代LMI方法有效地求解。鉴于模糊奇异摄动模型能够将多时标非线性系统通过隶属函数转变为一系列多时标线性系统的插值，适用于多时标线性系统的方法可以通过适当的变化用于非线性奇异摄动系统中。为减少LMI或BMI方法求解控制器的保守性问题，提出一种基于模糊奇异摄动模型的自适应控制器，用于存在不确定性的带挠性附件航天器的跟踪控制中，采用Lyapunov方法保证闭环系统的稳定性。仿真结果证明，所设计的控制器能够获得较好的跟踪效果［10－12］。

以上提出的控制方法，绝大多数要求模糊奇异摄动模型的规则后件或者部分或者完全已知，这在实际系统中，有时很难达到。为此，本文将进一步深化研究奇异摄动系统的控制问题。当模糊奇异摄动模型的规则后件参数完全未知时，提出一种直接型自适应控制器，其中状态反馈的增益可以在线调整。最后将此控制器用于后件参数未知的模糊奇异摄动系统的模型跟踪控制中，并与初始条件及参考模型相同但后件参数已知情况下设计的鲁棒控制器相比较，仿真结果证明了该自适应控制器的有效性。

1 问题阐述

设一大类奇异摄动系统如柔性机械手能够由以下数学模型进行描述:

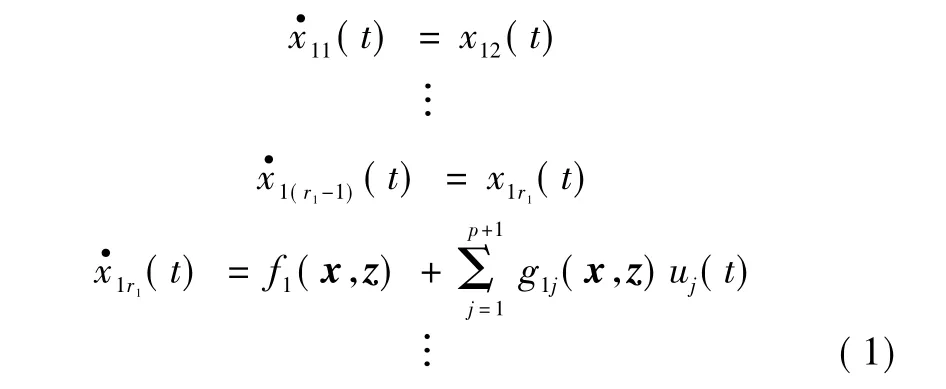
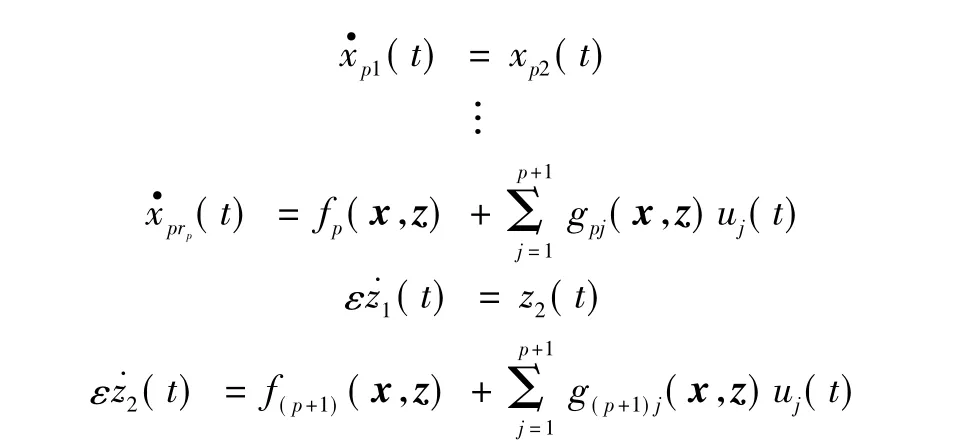
其中:ri是子系统的相对阶rp+1=2。x(t)和z(t)分别是快慢状态向量;x(t)=和为控制输入;fi(x，z)，gij(x，z) 为未知函数;ε是小的正数。

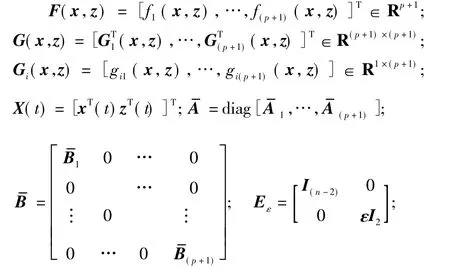
(1)可以写成

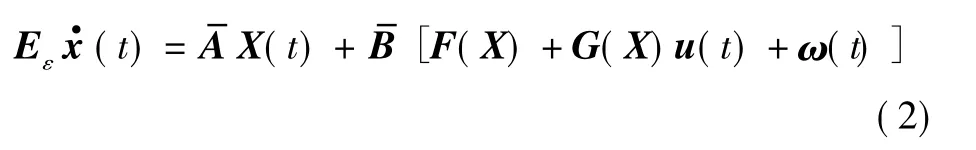
系统(1)、系统(2)可以建立由一系列“如果－则”规则描述的模糊奇异摄动模型。假设第l条规则如下。

Rl:如果v1是且…且vN是ΨlN，则

给定输入输出对x(t)和u(t)，TS模型可以合成为

这里xm(t)∈Rn表示参考模型的状态，r(t)∈Rp为有界参考输入。

定义跟踪误差为

控制目标即设计控制器u(t)，使得被控对象的状态x(t)跟踪稳定参考模型的动态xm(t)，即当t→∞时，e(t)→0。

2 自适应控制器设计及稳定性分析

由于矩阵Hl和Ll未知，假设此时的理想控制律为

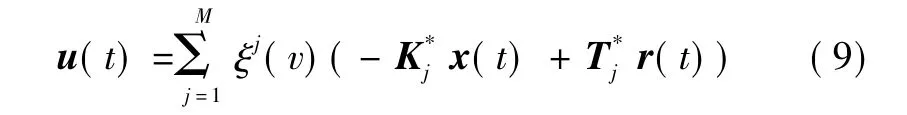
则可得闭环系统为

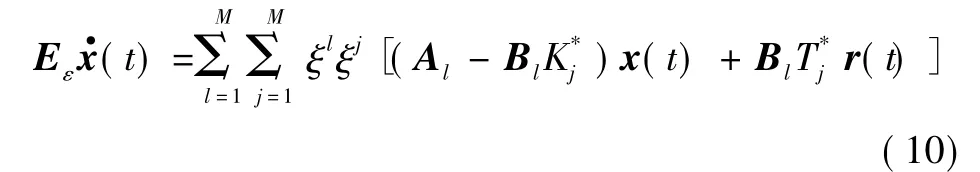
则闭环系统等价于式(7)，因为式(7)为稳定系统，则有当t→ ∞ 时，e(t)→0。

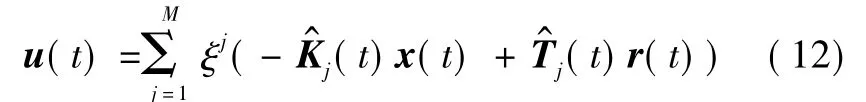
对式(8)求导得

将式(12)代入式(13)，可得

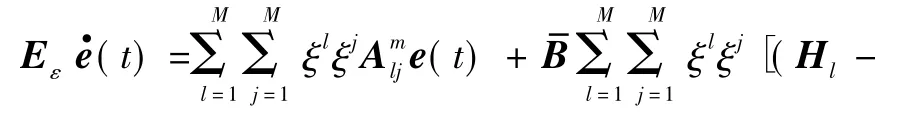
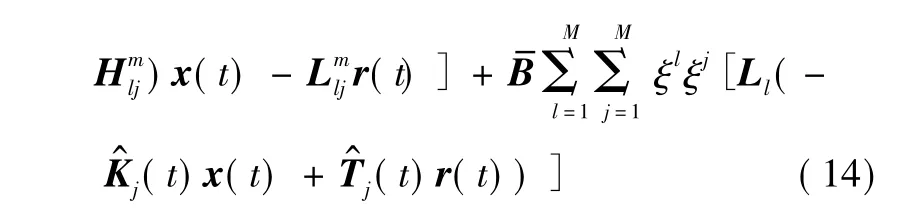
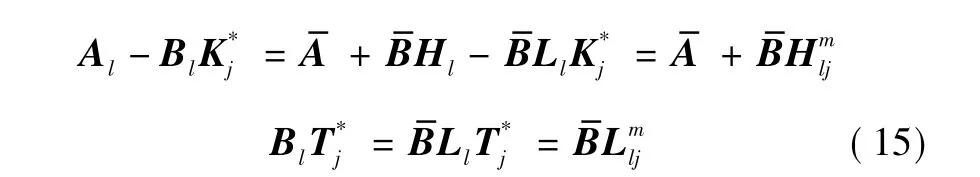
则有

所以式(14)即为

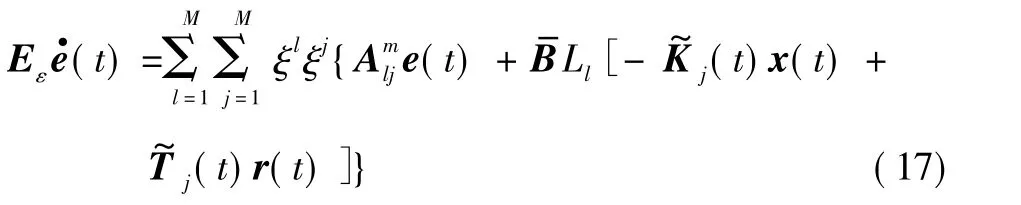
对式(18)求导得

取自适应律为

将式(21)、式(22)代入式(20)得

由此得到定理1。

定理1考虑式(3)所示的被控系统和稳定参考模型(6)，采用控制律(12)和自适应律(21)、(22)，假设参考输入r(t)和参考状态量xm(t)一致有界，则能够保证在控制量和输入信号有界的情况下，当t→∞时，e(t)→0。

证明:由式(23)得，对于任意的 t＞0，有 e(t)，有界。因为xm(t)有界，则X(t)有界。又因为r(t)∈L∞，根据式(12)得u(t)∈L∞。因此闭环系统的所有信号有界。所以

由式(23)可以得到

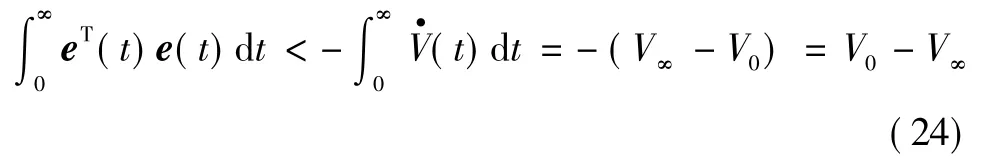
因此有e(t)∈L2。

由于小参数ε的存在，在求解LMI的过程中会存在病态。可以令式(19)变化为不等式

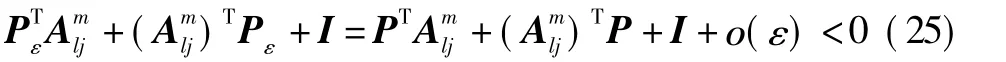
只要使得公共矩阵P满足式(26)

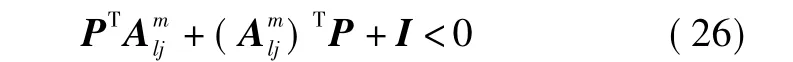
讨论:设计参考模型(6)的首要条件是稳定，其次需满足线性矩阵不等式(19)。在参考模型稳定的基础上，式(19)中的Pε应该很容易求得。最后在保证以上两个基本条件的前提下，可以通过选取不同的参考输入r(t)和参考模型的矩阵参数，以达到优化跟踪系统的动态性能的目的。例如，可以通过增加矩阵Am特征根的数值，提高闭环系统的响应速度。

3 仿真验证

本部分将设计一种自适应控制器，使得即使模糊奇异摄动模型的规则后件参数未知，闭环系统仍然能够跟踪稳定参考模型的状态。假设该模糊奇异摄动模型由两条规则建立，其规则如下所述。

Rl:如果x1(t)是，则

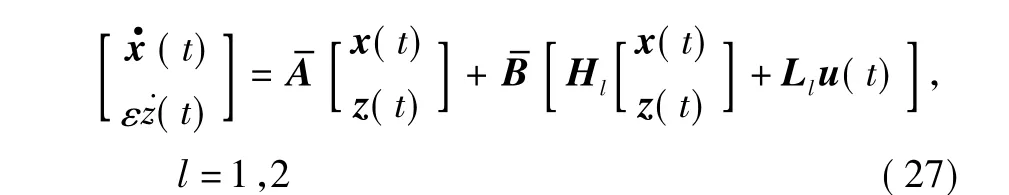
这里

则可得

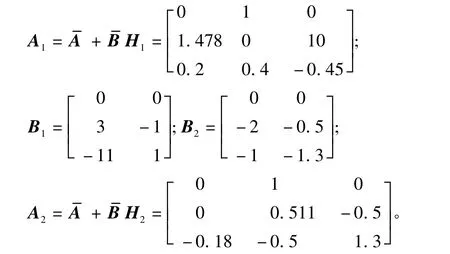
假设隶属函数为

稳态参考模型的参数为

假设 ε =0.11，求解式(19)得

这里参数 A1，A2，B1，B2未知，需要按照式(12)和式(21)、式(22)设计控制律和自适应律，仿真结果如图1～图5的实线部分所示。为了便于比较，同时假设模糊奇异摄动模型的参数已知，对系统设计鲁棒控制器，仿真结果如图1～图5点划线部分所示。

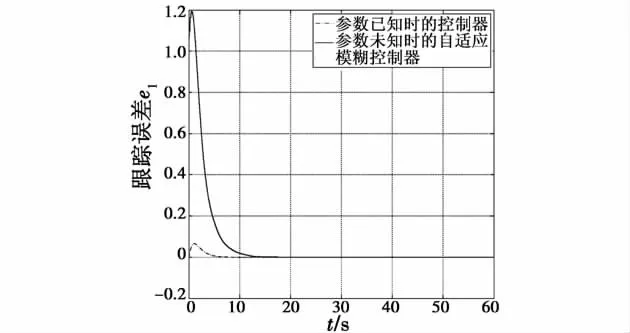
图1 跟踪误差e1(t)Fig.1 Tracking error of e1(t)

图2 跟踪误差e2(t)Fig.2 Tracking error of e2(t)

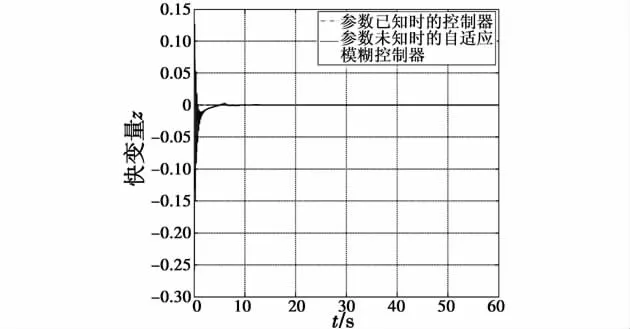
图3 快变量z(t)Fig.3 Fast variable of z(t)

图4 控制量u1(t)Fig.4 Controller of u1(t)

图5 控制量u2(t)Fig.5 Controller of u2(t)

从图1～图5可以看出，与模糊奇异摄动模型规则后件参数已知时采取鲁棒控制所得到的仿真结果相比，采用本文提出的方法使得闭环系统的超调量和调节时间都略有增加，原因在于本章提出的方法是基于模型规则后件参数未知情况下提出的，控制器的增益需要通过自适应调整才能达到稳定值。虽然如此，在15 s以后，控制器输出仍然能够达到稳定，系统的慢状态较好地跟踪了参考模型的状态，而快状态能够保持稳定。

4 结论

本章提出当模糊奇异摄动模型的参数完全未知情形下的自适应跟踪控制，不需要模糊奇异摄动模型精确已知，控制器的增益值可以在线自适应调整，仿真结果证明了方法的有效性。

［1］ GAJIC Z，LIM M T.Optimal control of singularly perturbed linear systems and applications-high accuracy techniques［M］.New York:Marcel Dekker，Inc，2001.

［2］ CHOW J H，KOKOTOVIC P V.A decomposition of nearoptimum regulators for systems with slow and fast modes［J］.IEEE Trans.on Automatic Control，1976，21(5):701-705.

［3］ ZHANG X Y，JIN H Z，ZHANG H P，et al.Robust sliding mode control for a class of uncertain nonlinear singularly perturbed systems［C］//Proc.of the 41st SICE Annual Conference，2002，4:2616-2621.

［4］ LIU H P，SUN F C.Survey of singularly perturbed systems:Theory and application［J］.Control Theory and Applications，2003，20(1):1-7.

［5］ SPOONER J T，PASSINO K M.Stable adaptive controls using fuzzy systems and neural networks［J］.IEEE Transaction on Fuzzy System，1996，4(3):339-359.

［6］ TANAKA K，WANG H O.Fuzzy control systems design and analysis:A linear matrix in equality approach［M］.New York:Wiley-Interscience Publication，John wiley ＆Sons，Inc，2001.

［7］ LIU H P，SUN F C.Controller design and stability analysis for fuzzy singularly perturbed systems［J］.Acta Automatic Sinica，2003，29(4):494-500.

［8］ LIU H P，SUN F C.H2state feedback control for fuzzy singularly perturbed systems［C］//Proc.of the 42nd IEEE conference on decision and control，Maul，Hawali USA，2003:5239-5243.

［9］ LIU H P，SUN F C.Simultaneous stabilization for singularly perturbed systems via linear matrix inequalities［J］.Acta Automatic Sinica，2004，30(1):1-7.

［10］ LI Li，SUN Fuchun.An adaptive tracking controller design for non-linear singularly perturbed systems using fuzzy singularly perturbed model［J］.IMA Journal of Mathematical Control and Information，2009，26(4):395-415.

［11］ LI Li，SUN Fuchun.A reference model based adaptive fuzzy controller for nonlinear dynamic systems［C］//FSKD，2009，4:37-41.

［12］ 李莉，孙富春.自适应模糊奇异摄动控制在航天器中的应用［J］.电光与控制，2009，16(10):62-65.