不确定性修正的相似性测度关联算法

黄伟平， 徐 毓， 王 杰

(1.空军雷达学院，a.研究生管理大队; b.科研部，武汉 430019; 2.中国人民解放军95174部队，武汉 430019)

0 引言

分布式系统结构由于对信道容量要求低、生命力强、在工程上易于实现而得到很大重视。在分布式结构的信息融合系统中，每个传感器都有自己的处理器，形成局部航迹，再在融合中心对各局部航迹进行分配组合，形成系统航迹。在此过程中的航迹关联算法通常有基于统计［1－2］和模糊数学［3］的方法两大类。相似性测度的航迹关联算法是典型的基于模糊数学的方法，该方法基于模式识别思想提出［4］，将各传感器中的任意航迹视为一个模式，把航迹关联问题转化为模式匹配问题，根据航迹整体走向判断相关性，完成对各局部航迹的分配，关联效果较好［5］。

但是，由于传感器对目标跟踪具有信息的不完整性、不准确性，并存在虚情和漏情，而且目标及其存在环境的诸多信息也难以为数据关联所充分掌握或应用，每个时刻各航迹的相似性测度会存在一定的误差［6］，也就是说，航迹关联判决所依据的统计量不都是可靠的，存在不确定性。“航迹相似性测度”及其“航迹关联不确定性”都是航迹关联信息的重要组成部分［7］，它们共同构成完整的航迹关联信息。在航迹关联不确定性方面，Blackman［8］定性地将跟踪关联问题空间划分为3个区域:正确关联区域、不稳定区域和错误关联区域。因此，在相似性测度的计算中，获取航迹关联对的不确定性描述，以判定两条航迹产生于同一个目标的可疑程度，并对航迹对的关联相似性测度进行修正，对提高情报融合系统的自适应能力和精确性具有一定的应用价值。

本文将对引起航迹关联对不确定性的因素进行分析，并构造相应的修正因子以表示多条航迹关联对来源于同一个目标的可疑程度。在关联判决中，利用不确定性因子对航迹关联对的相似性测度进行修正，以减小不确定因素对航迹关联的不利影响。本文算法的研究路径为:首先，计算各航迹间的归一化相似性测度，采用相似性测度阈值条件来挑选航迹关联对，形成待确定航迹关联对;接着，评价作为关联决策依据的航迹整体相似性测度计算过程中的不确定性;然后，分析引起航迹关联不确定性的因素，根据各不确定性因素，计算相应的修正因子;进而，基于修正因子对航迹相似性测度进行修正，利用修正的相似性测度极大化条件，确认最终的正确关联组合。

在航迹关联中，增加航迹关联不确定性分析环节，利用关联不确定性因子对航迹关联相似度进行修正，利用修正的航迹相似性测度作为关联判断统计量，能有效减小系统误差参数、虚情或漏情等不确定因素对航迹关联的不利影响，得到更低错误关联率，仿真实验验证了算法的有效性及可靠性。

1 模式识别的航迹关联

设传感器i跟踪ni个目标，其航迹号集合为ϑi={1，2，…，ni}，在时间t上对第p个目标的状态估计形成的航迹为Xip(t)，p∈ϑi，估计误差协方差为vip(t);传感器 j跟踪 nj个目标，航迹号集合为 ϑj={1，2，…，nj}，对第q个目标的状态估计形成的航迹为Xjq(t)，q∈ϑj，估计误差协方差为vjq(t)，且两传感器误差独立。

1.1 关联步骤

1.1.1 待关联航迹

在传感器i和传感器j共同探测区域内，以待关联航迹Xip(t)为中心，取一个适当大小的连通区域，并以U表示该区域内所有航迹的集合。定义时间t上待关联航迹集合为:A(t)={(Xip(t)，Xjq(t))|Xip(t)∈U，Xjq(t)∈U};传感器i、传感器j的待关联航迹集分别为

在数据关联看来，一个航迹通常与另一传感器的多条航迹、而不是仅与一条航迹有相关的可能性。多传感器航迹关联关系可以用关联矩阵表示:

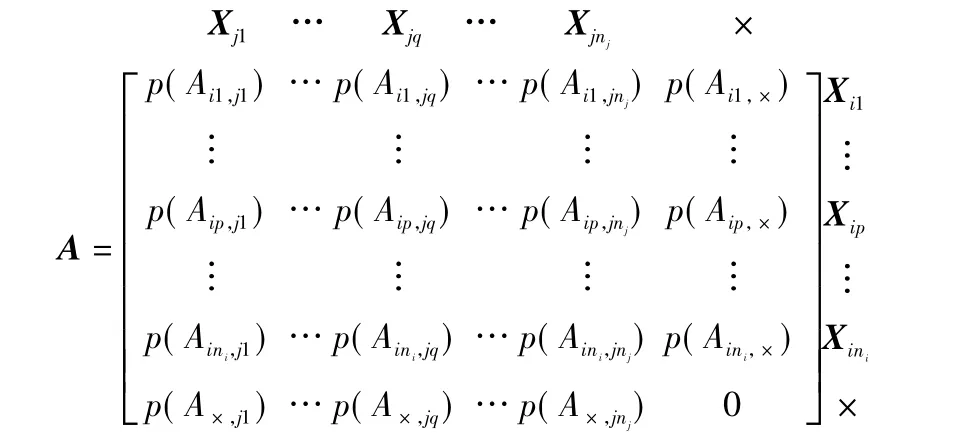
其中:×表示不存在的航迹;Aip，jq表示航迹Xip和航迹Xjq来源于同一个目标(或虚警)的事件;Aip，×表示Xip不对应于另一传感器的任何航迹的事件;p(Aip，jq)表示事件Aip，jq发生的概率，在基于模式识别的航迹关联算法里，p(Aip，jq)即为相似性测度 aip，jq。

1.1.2 统计距离

定义 rip，jq(k)=Xip(k) － Xjq(k)，其维数为 N。假设rip，jq(k)服从高斯分布，则其协方差矩阵为v(k)的各元素为

定义Xip(t)、Xjq(t)两航迹在k时刻的统计距离为

1.1.3 航迹总体相似性测度

定义在k时刻的模式相似性测度为

其意义是:在k时刻航迹间的距离越小，则数据间的相似性测度越大。故把1～(k－1)时刻的航迹相似性测度组成航迹相似性向量:

则航迹Xip(t)与航迹Xjq(t)到k－1时刻为止的总体相似性测度［5］为

进而得到下面递推式

1.1.4 归一化航迹相似性测度

分别计算Xip(t)与集合Aj(t)中每一个航迹的相似性测度，并构成向量:

定义归一化航迹相似性测度

式中:‖aip(t)‖1表示向量aip(t)的1－范数。

1.1.5 待确认航迹关联对

在航迹间总体相似性测度的基础上，采用相似性测度阈值条件来挑选航迹关联对。即若

1.2 性能分析

事实上，在时间t上传感器i和传感器j的两航迹Xig(t)和Xjh(t)来源于同一真实目标(用T标识)概率为

则其概率密度函数为

在基于模式识别的数据关联算法中，通常将Xig(t)和Xjh(t)的相似性测度Lig，jh(t)定义为f(Xig(t)，Xjh(t)|T)，并以之作为关联判决的依据。

式(10)、式(11)说明，航迹Xig(t)和Xjh(t)来源于同一真实目标的概率不仅与Lig，jh(t)或p(Xig(t)，Xjh(t)|T)有关，还与反映目标的存在与分布情况、反映传感器的探测性能的p(T)、p(Xig(t)，Xjh(t))有关。可见，基于每个时刻Lig，jh(t)作出关联决策的航迹整体相似性测度，其关联航迹并不一定以较高概率来源于同一真实目标，需要对航迹的相似性测度进行修正。

2 引起航迹关联不确定性的因素分析

航迹在某时刻相似性测度的不确定性产生于传感器对客观世界感知的不完全性。传感器对目标探测信息的不完整、不精确、不准确，信源存在虚情、漏情及探测范围受限，以及传感器工作特征参数未确知等因素，造成一个传感器探测的某一航迹与另一传感器的零条或多条航迹的不确定区域出现重叠，使得航迹的关联存在多种可能性，从而导致关联决策具有必然的不确定性［9］。下文就引起关联不确定性的几种情况进行分析。

2.1 传感器的未检测区域

一个传感器对某一目标的感知不确定区域与其他传感器未感知区域存在重叠关系，会导致航迹关联存在不确定性。图1示意的是电子侦察E1与雷达R1构成的探测系统。由于电子侦察的感知范围往往大于雷达的感知范围，电子侦察侦测的辐射源不一定位于雷达的探测范围内，即便存在雷达探测目标T1、T2与辐射源Tb的方位线相距很近，判定Tb与T1或T2关联显然是不正确的。

图1 传感器未感知区域导致的关联不确定性Fig.1 The uncertainty brought by the undetective area of the sensor

2.2 传感器的漏情和虚情

传感器都有一定的虚、漏情率，可按漏情率虚拟出若干个航迹作为漏情，任一航迹信息都可能是虚情，传感器的漏情和虚情也是引起航迹关联不确定性的重要因素。

2.3 传感器参数的未确知性

当对传感器的系统误差参数不确切掌握，而仅知道其范围的情况下，通常用常值随机过程来描述传感器各独立测量方向的系统误差。图2示意的是传感器R2存在较大的系统误差且其参数未知的情况。系统误差使得传感器的目标感知不确定区域变大、且航迹明显偏离目标的真实状态，从而导致不同传感器对不同目标(如Ta与T2)的感知不确定区域出现重叠，造成航迹关联问题复杂化。因此，在分析引起关联不确定性因素的过程中，有必要区分传感器的系统误差和随机误差的影响［1－2］。

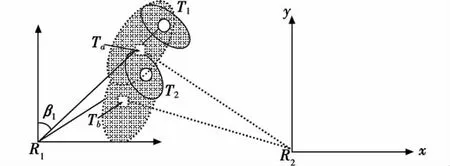
图2 传感器系统误差和目标密集分布导致关联不确定性Fig.2 The uncertainty brought by system error of the sensor and dense distribution of the target

2.4 目标信息的不准确性

由于传感器具有不同分辨率，在实际工作存在缺维探测等现象，因此，vip，jq(t)的取值存在一些误差，从而影响统计距离的准确性，这也将增加相似性测度的不确定性。

图3所示的是两个二维雷达对两个空中目标探测的情况。图中，β表示目标的方位，ε表示目标的仰角。由于二维雷达不能提供目标仰角信息，使得两个雷达R1、R2对两个目标的感知不确定区域互相重叠，造成航迹关联环节没有充分的信息判定两个目标的相对位置关系(T1、T2情况下的等高关系或Ta与Tb情况下的高低关系)，导致关联判别存在很大的不确定性。

图3 缺维探测导致的关联不确定性Fig.3 The uncertainty brought by the incomplete detection

图4 示意的是两个具有不同分辨率的雷达对水面目标的感知情况。将雷达R1与雷达R2感知的目标信息进行关联时，若按照传统的一对一关联的原则，无论是将Ta分配给T1还是T2都是不恰当的，都存在较高的关联不确定性，都将对后续的融合处理产生负面影响。

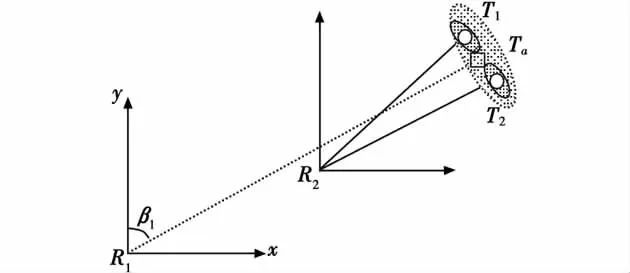
图4 不同分辨率导致的关联不确定性Fig.4 The uncertainty brought by the unmatched resolving power

3 修正的航迹关联相似度

分析传感器探测的目标探测性能对航迹关联判决的影响，计算两传感器各航迹间的不确定性修正因子，以去偏差后的统计距离用于描述航迹的相似性测度，综合虚情、漏情等多传感器探测信息的不一致性对航迹关联判决的影响，形成航迹关联相似度的修正值，确认最终的航迹的关联对。

3.1 描述未检测区域

假设以状态空间中的一个连通区域Ω来表示传感器对目标测量的不确定性。若传感器i对目标p的探测不确定区域不完全被传感器j的探测范围覆盖，以Ωip表示传感器i对目标p的探测不确定区域，以Ωip，j表示 Ωip被传感器 j的探测范围所覆盖的部分，以表示目标在 Ωip条件下落入 Ωip，j的概率，则定义传感器j关于航迹Xip(t)未检测区域的计算因子

该值可以根据传感器探测指标及相对位置估算。

3.2 描述漏情、虚情的修正因子

3.3 修正传感器系统误差

定义

对集合Ac中的传感器i和传感器j的待确认关联对集合 Ad={(Xig，Xjl))|l∈aj}，其中其元素的个数为nd，采用式(14)统计偏差矢量dl(t)，其中，l=1，2，…，nd，构成统计偏差矢量集合:

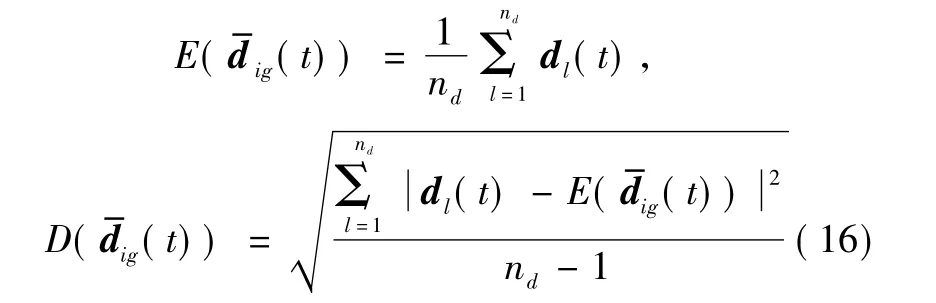
通过对待确认关联航迹对的统计偏差分析能克服传感器系统误差对关联统计距离的影响。

3.4 修正的相似性测度

基于式(14)、式(16)定义Xig(t)的修正统计距离

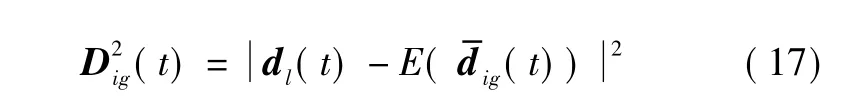
将修正后的统计距离代入式(3)～式(8)，得到修正的相似性测度 aig，s(t)，同样的，可以计算 as，jh(t)。结合式(13)、式(17)，形成两航迹 Xig(t)、Xjh(t)关联相似度修正模型［10］:

4 关联确认

在阀值挑选寻找出来的待确认航迹关联对集合Ac的基础上，采用相似性测度最大化的准则来确认航迹关联的判断。即若

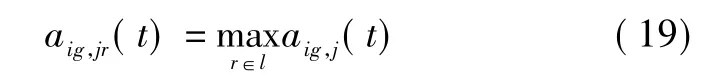
则判断航迹Xig(t)与航迹Xjr(t)在时刻k相关。且航迹Xig(t)不再与aj中其他航迹相关，对应的航迹Xjr(t)亦不再与ai中其他航迹相关，将航迹Xig(t)，Xjr(t)从待确认航迹关联集中去掉，继续下一条航迹的确定，直至全部航迹关联完毕。

5 仿真验证

模拟2部雷达对5批空中飞行目标进行探测的场景，目标雷达、目标的位置及编号如图5所示。在仿真实验中，雷达在各独立测量方向上的误差模型为

其中:es(t)为常值系统误差项;ec为周期性系统误差的幅度;β(t)表示目标的方位;er(t)为随机误差项。两个雷达的距离ec均取为60 m，方位ec均取为0.3°，距离er(t)的标准差均取为40 m，方位er(t)的标准差均取为 0.2°。

图5 雷达和目标分布示意图Fig.5 The distribution of the sensor and the target

从图6、图7可以看出，基于相似性测度的航迹关联算法对目标航迹的关联均能取得较低的错误率，但修正的关联算法由于考虑到目标关联过程的不确定因素，通过各不确定因子的修正，错误关联率更低，能取得更好的关联效果。

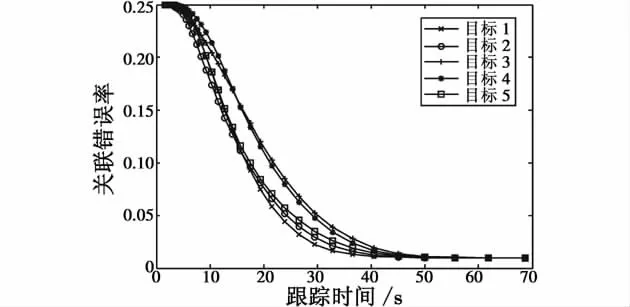
图6 相似性测度的关联错误率Fig.6 The false probability of the similarity degree method

本文提出的修正航迹关联算法，一方面基于航迹相似性测度计算过程中的不确定性因素，对作为关联依据的统计量进行了修正;另一方面，在航迹关联对匹配的过程中，采用阀值初选和极大值确认两个环节进行关联确认，航迹关联的错误率也随之降低，说明本文采用的相似性测度修正方法是有效且实用的。

图7 修正的相似性测度的关联错误率Fig.7 The false probability of the modified similarity degree method

6 结论

本文提出的修正航迹关联算法，以归一化航迹相似性测度为基础，综合考虑传感器的虚情、漏情、未检测区域以及传感器参数的未确知性等因素对航迹相似性测度关联的不利影响，对航迹关联相似性测度进行了修正。在航迹关联过程中，先采用阀值挑选出待确认航迹关联对，通过对待确认航迹关联对的统计分析，计算出引起航迹对不确定性因素的影响因子，用这些影响因子得到新关联统计量——修正的相似性测度，结合相似性测度极大化确认最终的航迹关联组合。仿真实验表明，修正的航迹相似性测度关联算法能得到目标更低的关联概率，为提高系统航迹的鲁棒性、精确性奠定了基础。

［1］ 孙俊生，王建民，王维锋.多传感器多目标联合概率数据关联研究［J］.信号与信息处理，2009，39(11):19-21.

［2］ 杨哲，韩崇昭，李晨，等，基于目标之间拓扑信息的数据关联方法［J］.系统仿真学报，2008，20(9):2357-2360.

［3］ 胡傲，冯新喜，王冬旭，等.遗传模糊聚类算法在数据关联中的应用［J］.电光与控制，2010，17(3):30-34.

［4］ 蔡元龙.模式识别［M］.西安:西安电子科技大学出版社，1992.

［5］ 黄伟平，徐毓，王杰.综合运用模式识别与回归分析的数据融合算法［J］.控制与决策，2010，25(1):110-115.

［6］ BAR-SHALOM Y，BLAIR W D.Multitarget-multisensor tracking applications and advances［M］.London:Artech House，2000.

［7］ KLIR K G.Uncertainty and information:Foundations of generalized information theory［M］.Hoboken:John Wiley ＆ Sons，Inc.，2006.

［8］ BLACKMAN S.Multiple target tracking with radar applications［M］.Norwood，Ma:Artech House，Inc.，1986.

［9］ 林洪桦.测量误差与不确定度评估［M］.北京:机械工业出版社，2010.

［10］ BAR-SHALOM Y，CHEN H.Multi-sensor track-to-track association for tracks with dependent errors［C］//The 43th IEEE Conference on Decision and Control，Paradise Island，Bahamas，2004:2674-2679.