优美的摆线——2011年高考数学江西卷理科第10题赏析

332100 江西省九江第一中学 江民杰

2011年高考已落下帷幕，江西卷理科第10题及文科第10题立意新颖，构思独特，其内容涉及摆线，是教材内容的延伸，较大程度考查了学生数学能力.本文以理科第10题为起点，进一步认识摆线及其方程.

1 赏析

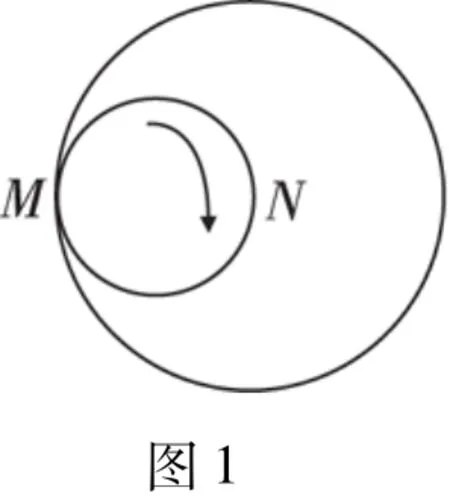
(2011年江西)如图1，一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动，M和N是小圆的一条固定直径的两个端点.那么，当小圆这样滚过大圆内壁的一周，点M，N在大圆内所绘出的图形大致是

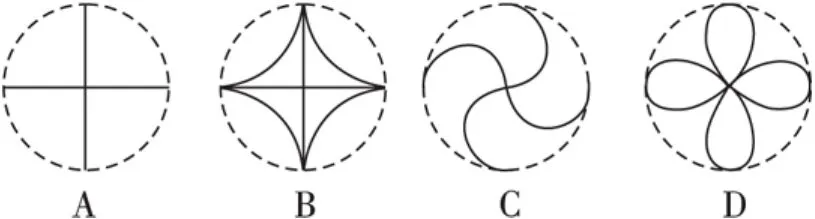
解 方法1 特殊位置可选A.

由平面几何知，两圆内切，故点N，O2，P三点共线，

故NP为小⊙O2的直径，从而∠PM'N=90°，

又∵∠MNP=θ，故PM'⊥x轴.从而M'必在x轴上，故M点的轨迹为y=0(-1≤x≤1)同理N点的轨迹为x=0(-1≤y≤1)，选 A.

2 溯源

我们知道：一个圆在平面内沿着一条直线无滑动地滚动，我们把圆周上一定点的运动轨迹叫做平摆线.教材选修4-4专门讨论了平摆线.

实质上，本题就是历史上著名的卡丹问题：当一个圆盘沿一个半径是它2倍的圆内无滑动地滚动时，小圆上一点画出怎样的图形.

如果我们不限制小圆半径和大圆半径的关系，那么更一般的情况是怎样呢?

一个动圆在定圆内无滑动滚动时，动圆上一定点的运动轨迹叫做内摆线.

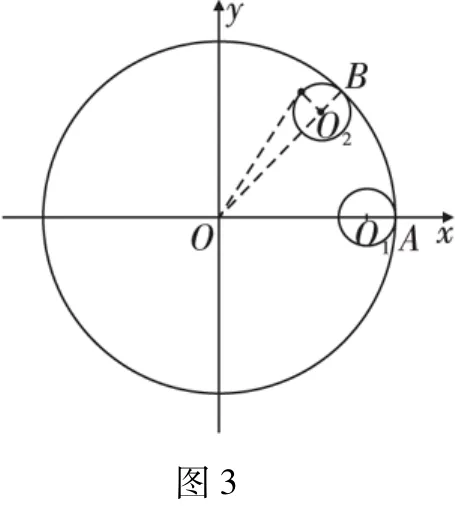
如图3所示，设定⊙O半径为R，动圆半径为r，取定圆圆心O为原点，点A为动圆圆周上所规定的一个定点，并记A点是动圆开始滚动时与定圆的切点，以OA为x轴，建立直角坐标系，当动圆滚动到与定圆相切于B点时，A点相应运动到A'点，令∠AOB=t.

则内摆线的参数方程为

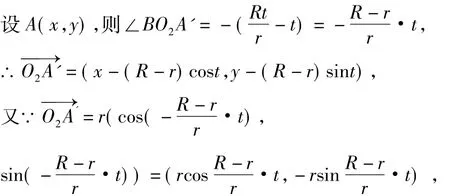
则得到动点A的轨迹方程为

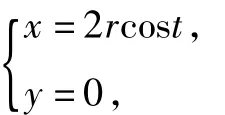
即y=0(-2r≤x≤2r).

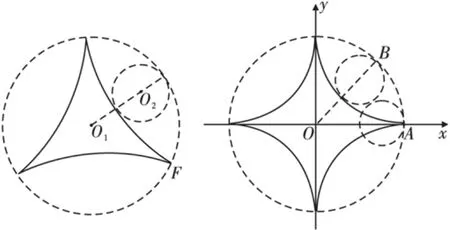
图4

本题就是R=2r时内摆线的特例.

实际上，一个动圆在定圆外无滑动滚动时，动圆上一定点的运动轨迹叫做外摆线.读者可类似推出其参数方程.

3 思考

本题作为新课改首次高考题，立意新颖，既能较好地考查学生的能力，又体现了新课程改革的理念.本题是选修教材4—4《平摆线》内容的延伸，做到了源于课本、高于教材，体现了公正公平.近年来，全国统一高考江西卷每年都设计几道立意新颖的试题(如解析几何题，每年都在经典几何中披挂那些有趣味的定理，如2008年文科的蝴蝶定理、2009年文科的彭色列闭形定理，值得回味与关注)，这种命题思路有利于中学数学的教学，有利于培养学生后续数学学习能力.因此，我们进行高考复习指导时，要减少大规模的强化训练，紧扣新课程标准，以教材为本、夯实基础;要设计一些好的研究性课例，引领学生思考分析、感受过程、培养学生动手观察，解决问题的能力;平时测试要设计一些动手实践的试题，培养学生学习数学的兴趣，激发学生探究问题的本质，体现新课程改革的精神，真正做到减轻学生的负担.