基于双谱分析的毫米波多普勒引信目标检测

王新会

（机电动态控制重点实验室，陕西 西安 710065）

0 引言

目标检测和识别就是指从目标的回波信号中提取目标的有关信息和特征，进行综合判断，判断目标的有无。复杂背景中引信信号的检测是多普勒引信信号处理的一个重要课题。双谱是高阶谱中阶数为三的一种特例，包含了目标的幅度和相位信息，能更完整地反映出目标的本来特征。

毫米波多普勒引信目标回波实际上是一随机过程，谱估计是一种有效的分析工具。传统的功率谱（相关函数）等方法在无线电引信回波信号的处理中，从过程中提取的是满足假设高斯条件的信号；想充分了解信号的非线性、非高斯带来的信息，仅用二阶累积量是不够的，这样对信号的特征分析及检测存在一定的不足。有文献采用双谱分析检测目标，文献［1］解决了利用积分双谱在相位方面特征进行雷达信号的目标识别的目的，体现了双谱复特征的优越性，但对象是雷达，与引信不同。文献［2］解决了混杂在噪声里的微弱信号检测，体现了高斯噪声下双谱为零特征的优越性，但其载频较低。文献［3］解决了在强背景噪声下，检测调频引信中的微弱信号，体现了在非高斯AR模型下，参数化双谱的估计的优越性，但没有涉及多普勒引信。本文将双谱分析的目标检测方法引入毫米波多普勒引信。

1 双谱分析用于引信信号的检测

1.1 双谱分析的基本理论

双谱的定义为三阶累积量的二维离散时间傅里叶变换［4－6］，双谱存在的条件是三阶矩绝对可求和，平稳时间序列的三阶累积量和双谱［5，7－9］可分别由下式表示：

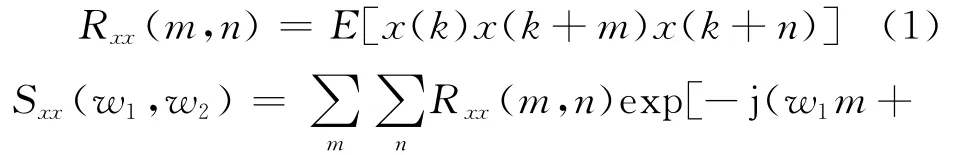
对于一个离散实际能量有限的确定信号可将双谱表示为：

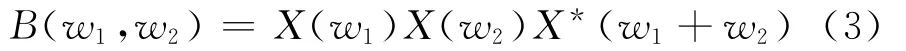
X（w）是信号在x（n）在频率点w的傅里叶变换，“＊”表示复共轭。由式（3）知双谱为复值谱，有2个频率变量w1和w2。在当双谱切片特征w1＝w2＝w，可得双谱对角切片，B（w，w）＝ X（w）X（w）X＊（2w），使特征降为一维信号，简化了运算。

1.2 采用参数化双谱估计方法对引信信号检测

在文献［3］中，是以正弦调频引信信号为例，采用参数化双谱估计，非高斯AR模型，在模型的基础上进行背景信号与目标信号的仿真，利用双谱分析可以很明显地看到双谱形状和谱峰位置均表现出了明显的差异，具体的双谱分析的调频引信信号原理框图如图1所示。

图1 调频引信双谱分析原理框图Fig.1 FM f uze bispectr u m analysis principle diagram

2 基于双谱分析的毫米波多普勒引信目标检测方法

毫米波多普勒双谱分析目标检测方法有别于参考文献［3］中的方法，跟图1的不同主要是利用非参数化双谱分析及双谱对角切片进行分析信号，通过实际的外场实测数据，通过双谱分析和双谱对角切片验证背景信号与目标信号所表现出的特征进行识别和特征信息进行目标识别。毫米波多普勒引信双谱分析原理框图如图2所示。

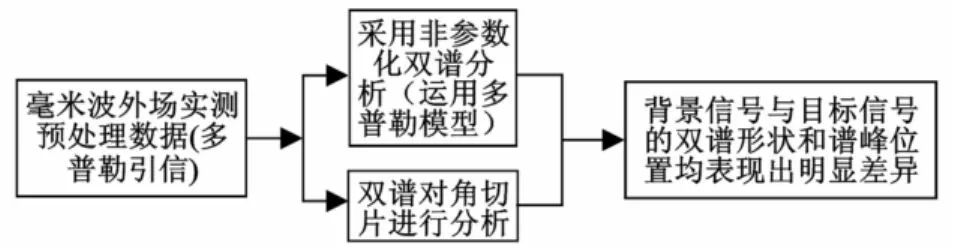
图2 毫米波多普勒引信双谱分析原理框图Fig.2 Millimeter wave f uze Doppler bispectrum analysis principle diagram

2.1 非参数化的双谱分析

在外场实测的目标回波信号分析中，毫米波多普勒引信的回波信号在严格意义上，其实是非平稳信号。而目标检测的实质是在非平稳过程中找到特定的规律来判断是目标信号还是背景信号。采用非参数化双谱分析的直接估计法，对毫米波引信信号进行目标特征提取来分析信号。

即将数据信号 ｛x（1），x（2），…，x（N）｝分成 K段，每段M个样本，即N＝KM，并对每段数减去该段的均值。如有必要，每段补零以适应FFT的长度M。设fs是采样频率，N0是总的频率采样数，则Δf＝fs／N0为两个频率采样点之间的间隔。分别计算每段的离散傅里叶变换（DFT）系数和每段DFT系数的三重相关。在此计算的是双谱信号特征幅度信息是三维特征，不便于机器的处理和识别。采用双谱幅度对角线元素作为特征信息，可以把双谱矩阵对角化，提取对角线特征信息，即双谱的投影和双谱对角切片的值，并分析目标数据与背景的对角切片有什么不同之处，根据表现出来的不同，从所给数据的K段双谱估计的平均值分析两类数据之间的差异。

通过分析可以看到，毫米波多普勒引信的双谱（幅度谱）在双平面的投影及双谱的三维图，噪声与杂波的幅度和信号的幅度相差较多，因而双谱能够很好地抑制噪声。同时双谱是原点对称的，估计数据参数和双谱谱峰位置作为目标特征，利用它们可以检测出目标信号。

2.2 双谱的对角切片

分析统计双谱分析的特点，并通过对毫米波引信外场实测数据的双谱对角及对角切片的分析可以看到，目标信号的幅度和非线性相位都可由双谱的对角切片获得，双谱的对角线含有丰富的目标信息，双谱和双谱切片都是二维复函数（如公式（3）所示），即它们具有幅度和相位，这是功率谱所不具备的。所以提取双谱对角线的一半作为目标检测的特征，计算仿真也较为简单。这样将双谱转化到一维，又使目标检测识别特征简化，便于分类器的构造，是一种简捷、有效的检测方法。

3 试验验证

利用外场实测的8 mm多普勒引信进行背景（草地）中的车辆目标的测试，采样率为30 k Hz，数据长度10 480点，将每个数据分成40段，每段为5 120点，目标与背景测试数据各取20组进行统计。目标及背景信号波形如图3所示，图4是对应的功率谱（相关函数）图，双频率平面图如图5所示，双谱三维图如图6所示，图7为双谱对角切片图。

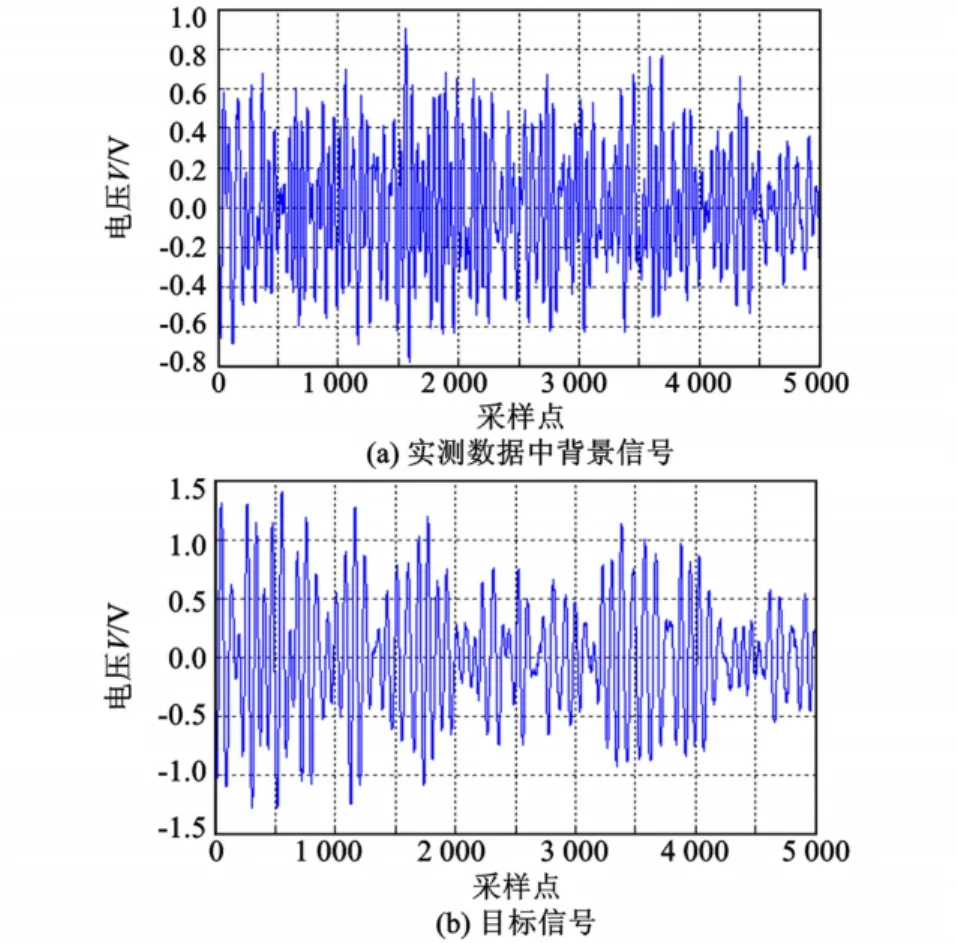
图3 毫米波多普勒引信测试原始图Fig.3 MMW f uze doppler test original figure

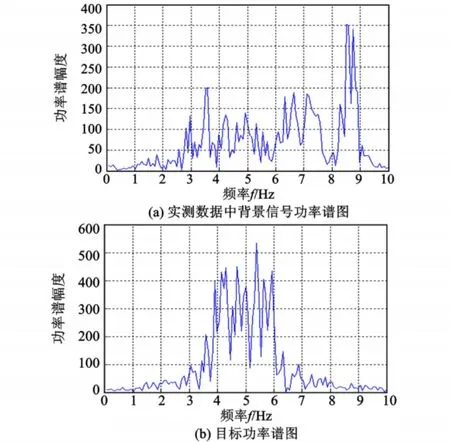
图4 毫米波多普勒引信功率谱图Fig.4 MMW f uze doppler spectr u m diagram

在图5和图6中，由毫米波多普勒引信双谱的特征图谱可知，信号能量主要集中于180 Hz、300 Hz，在外围400 Hz也有零星能量，（0，0）到（0.5 Hz，0.5 Hz）表示主频对角线的对角切片。图6中双谱三维图中背景的双谱幅值与目标的双谱幅值相差一个数量级。从图7中可以看出，该信号在0.078 Hz处具有峰值，并且峰值明显，分辨率高，曲线较为光滑，消除了部分噪声干扰；突出了信号的主要频率。图7是图6对应的双谱对角线切片的幅度信息，它很好地保留了单纯背景与目标的差异性，可以看出两个信号存在一定的个体差异，表明双谱很好地弥补了功率谱的不足，而且双谱的对角切片的谱峰位置和幅值参数构成目标特征矢量，可用于信号目标检测。

图5 不同情况下的双谱在f 1、f 2平面的投影Fig.5 In different conditions of bispectru m in f 1、f 2 plane pr ojection

毫米波多普勒引信目标回波存在明显的双谱谱峰，通过回波信号的双谱域特征处理，得到信号的能量信息；双谱的对角切片可以抑制部分噪声干扰，得到信号的幅度信息及信号的非线性性。通过分析，双谱毫米波引信背景信号和目标信号的双谱形状和谱峰位置均表现出明显差异，双谱的对角切片的谱峰位置和幅值参数可作为目标检测、识别的特征。

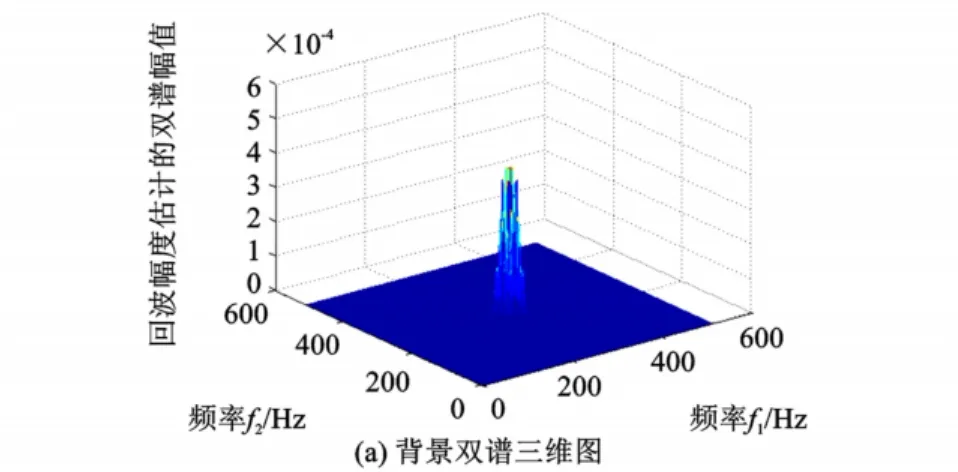
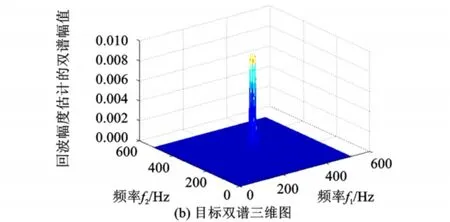
图6 双谱的三维图Fig.6 Bispectr u m of t hree-di mensional diagram

图7 双谱对角切片图Fig.7 Bispectr u m diagonal slices

为验证算法性能，选取20组毫米波多普勒引信信号，每组40次共80次试验，分别利用短时傅里叶（STFT）和双谱分析进行检测识别，分类器采用模式识别的线性分类器。其检测识别结果如表1所示。

表1 两种检测方法的识别率Tab.1 Two kinds of testing method recognition rate

从表1中可以看到，对于毫米波多普勒引信，双谱分析的目标检测识别率高于短时傅里叶变换。

4 结论

本文提出了基于双谱分析的毫米波多普勒引信目标检测方法。该方法通过采用双谱及双谱对角切片进行毫米波回波信号的特征分析及特征提取，利用提取的特征进行有无目标的判别。试验表明：双谱分析用于毫米波多普勒引信对复杂背景中地面目标检测的识别率高于短时傅里叶变换。但在信号检测过程中双谱特征的估计精度与数据长度有极大的关系，从而影响引信双谱特征的稳定，如何提高稳定的不变性特征，延伸双谱分析方法在毫米波多普勒引信中的实际应用，还有待于今后进一步地补充和完善。

［1］查品德.毫米波雷达回波去噪与特征提取研究［D］.哈尔滨：哈尔滨工程大学，2005.

［2］王凤歌，王辉，李晓荃.双谱在微弱信号检测中的应用［J］.中原工学院学报，2010，21（2）：5-7.WANG Fengge，WANG Hui，LI Xiaoquan.The application of bispectr u m in weak signal test［J］.Jour nal of Zhengzhou University of technology，2010，21（2）：5-7.

［3］易应萍，简金蕾.双谱分析在引信信号检测中的应用［J］.战术导弹技术，2006（1）：48-50.YI Yingping，JIAN Jinlei.The aplication of bispectr u m esti mation in f uze signal pr ocess［J］.Tactical Missile Technology，2006（1）：48-50.

［4］张贤达.现代信号处理（第二版）［M］.北京：清华大学出版社，2002.

［5］Zhang Gucci，et al.Extracting gear fault feature using integrated bispectrum［R］.International Conference on Robotics，Intelligent Systems Signal Processing，Changsha，China，2003.

［6］陈昌孝，何明浩，王志斌，等.基于双谱分析的雷达辐射源个体特征提取［J］.航天电子对抗，2007，23（5）：46-48.CHEN Changxiao，HE Minghao，WANG Zhibin，GAO Feng.Specific emitter feat ures extract based on bispectr um analysis［J］.Aerospace Electronic warfare，2007，23（5）：46-48.

［7］陈澎，任大孟.李呈杰.声背景下的信号检测方法研究［J］.信息技术，2003，27（6）：67-68.CHEN shu，REN Dameng，LI Chengjie.Study on signal detection method in noise background［J］.Inf or mation Technology，2003，27（6）：67-68.

［8］Cadzow J A.Blind Disconsolation via Cumulate Extreme［J］.IEEE Signal Processing Magazine，1996，13（3）：24-42.

［9］Nikias C L，Mendel J M.Signal processing with higheror der spectra［J］.IEEE Signal Pr ocessing Magazine，1993，10：10-17.