基于时延矢量封闭准则的多传声器降噪方法

吕艳新，顾晓辉

（南京理工大学机械工程学院，江苏 南京 210094）

0 引言

在战场环境下为了有效打击和摧毁敌方目标，需要对目标进行探测和识别，由于环境的特殊性和声探测技术的优良特性，目标的声探测技术得到越来越多的认可和发展。由于战场声目标的类型未知，多传声器采集到的多通道信号，没有目标的任何先验知识，可将其归为盲信号。采用传声器对信号进行同步采集的过程中，由于外界环境的干扰、仪器本身的噪声等造成盲信号中包含着不同程度的噪声，为了提取盲信号中的有效特征，需要对其进行降噪处理。传统的傅里叶分析方法［1］在处理此类信号时具有很大的局限性，它不能准确反映非平稳信号的时变特征。1998年美籍华人黄鄂提出了EMD（Empirical Mode Deco mposition，经验模式分解）理论［2］，该方法是一种自适应的时域信号处理方法，被认为是近年来对以傅里叶变换为基础的线性、稳态频谱分析的一个重大挑战与突破，主要用于非线性、非平稳信号的分析。EMD方法无需更多先验信息，可实时、高效、自适应的分解信号，并能够反映信号固有特征。EMD自提出以后，很多采用EMD进行信号降噪的方法也相继提出。有些降噪算法是基于信号噪声集中在高频成分的特性［3－6］，有些算法是对信号重构采用了I MF加权的方式［7－9］。

将EMD用于信号降噪，首先要明确分解得到的I MF函数是否包含有用的信号信息。最先研究I MF特性的是 Flandrin［10－11］和 Wu［12－13］等，他们都是基于统计特性对I MF函数特性进行研究，其中，Flandrin等人的研究是基于分形高斯噪声，而 Wu等人的研究是基于高斯白噪声。目前国内外提出的EMD降噪方法大都在已知噪声类型的基础上，针对单传声器信号进行研究，没有利用多传声器之间的融合信息。因此，提出基于时延矢量封闭准则的多传声器信号降噪方法。

1 EMD理论

EMD具有自适应的信号分解和降噪能力，其目的是根据非线性、非平稳信号本身的特征时间尺度将信号分解成有限个I MF和一个余项的和。I MF反映信号的内部特征，余项表示信号的趋势。每个I MF都是单分量的幅值或频率调制信号，且满足以下两个条件：

1）整个信号中零点数与极点数相等或至多相差1；

2）信号上任意一点，由局部极大值确定的包络线和局部极小值确定的包络线的均值均为零，即信号关于时间轴局部对称。

对任一实信号x（t）进行EMD分解的步骤如下：

1）首先确定信号x（t）上所有的极大值点和极小值点；然后，将所有的极大值点和极小值点分别用三次样条曲线连接起来，使两条曲线间包含所有的信号，确保不遗漏也不增添原信号的点，并将这两条曲线分别作为x（t）的上下包络线。计算出它们的平均值曲线m1（t），用x（t）减去m1（t），得

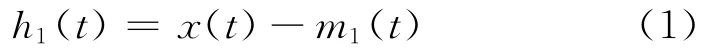
判断h1（t）是否满足I MF的两个条件。如果h1（t）不满足I MF的两个条件，需要把h1（t）作为原信号，重复上面的步骤得到h11（t），即：

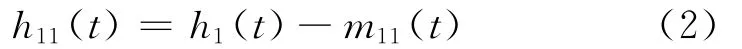
依次筛选k次，直到h1k（t）成为一个I MF，即：

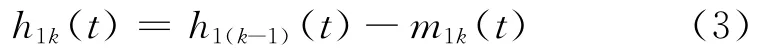
如此就从原信号中分解出了第一个I MF，称为第一阶I MF，记作：

2）从原信号中减去c1（t），得到第一阶剩余信号r1（t），即：

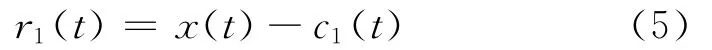
把r1（t）作为新的原信号，重复步骤1）。对后面的ri（t）也进行同样的筛选，这样依次得到第二阶I MF，…，第n阶I MF和第二阶剩余信号，…，第n阶剩余信号，

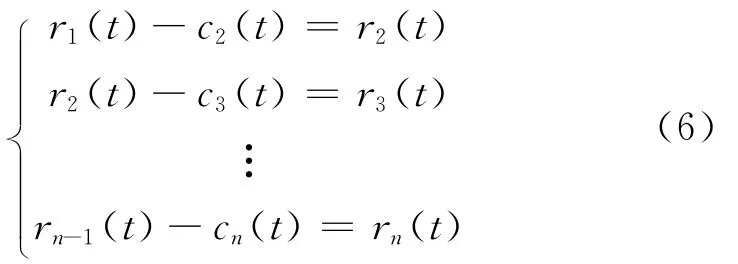
当第n阶I MF分量cn（t）或其余量rn（t）小于预先设定的值或rn（t）变成一个单调函数时，筛选结束。这样，由式（5）和式（6）得：

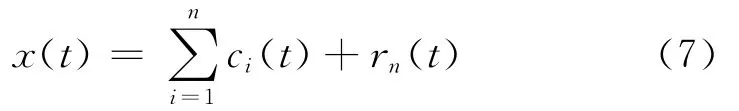
即原始数据可表示为有限个IMF和一个余项之和。I MF两零点之间的每一个波动周期中只有一个单纯的波动模式，没有其他叠加波，是EMD中分解信号的基本单元。I MF反映了信号中不同频率的成分，先分解出的IMF频率较高，后分解出的频率逐渐降低，至余项变为很低频率的脉动，即趋势项。下面给出某传声器接收到的信号EMD分解图，如图1所示。

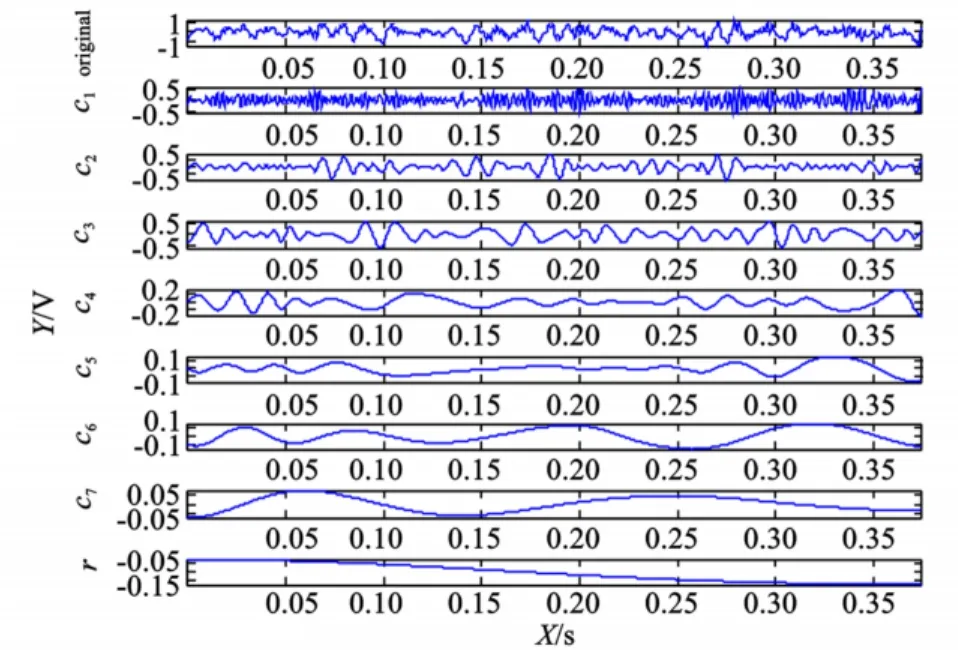
图1 某信号的EMD分解Fig.1 The EMD process of so me signal

图1 为传声器采集所得某段信号及其EMD分解过程，其中第一个图为采集得到的原始含噪信号，c1—c7为EMD分解得到的7个I MF分量，r为EMD分解最后的趋势项。

2 基于时延矢量封闭准则的多传声器信号降噪方法

依据多传声器时延估计特性，提出了时延矢量封闭准则，在此基础上研究了一种多传声器信号降噪方法。

2.1 时延矢量封闭准则

对于任意不处于同一条直线的3个点i，j，k，可以通过连线将其构成一个矢量三角形。假设矢量用d来表示，dmn表示从点m到点n的矢量，则上述矢量三角形可以表示为

如图2所示。

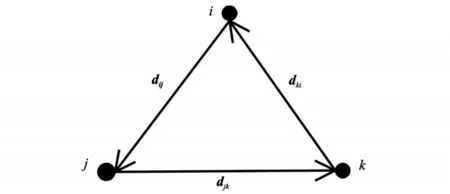
图2 矢量三角形示意图Fig.2 The diagram of vector triangle

如果在图2所示的3点i，j，k处分别放置3个传声器，声目标信号到达3个传声器的时间存在时延差，如图3所示。通常声源距离传声器组的距离远大于各传声器的相对距离，因此，各传声器时延之间的关系类似于矢量封闭三边形，即

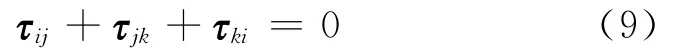
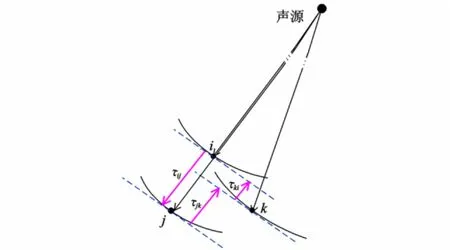
图3 时延矢量封闭三角形示意图Fig.3 The diagram of ti me delay vector close triangle

结合上述矢量三角形的特点，对传声器组进行布置，保证任意3个传声器不处于同一波阵面上。若传声器组包含有N（N≥3）个传声器，以某一传声器为基准，逆时针（或者顺时针）对传声器进行标号，分别为1、2、…、N，则有时延矢量封闭多边形，即，

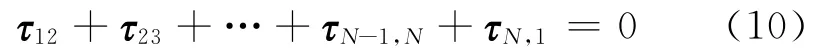
文中定义式（10）所表达的时延矢量封闭多边形为时延矢量封闭准则（TDVCR）。

2.2 基于TDVCR的多传声器降噪方法

各传声器信号EMD分解后同一I MF尺度内不同传声器信号时延值理论上也应满足时延矢量匹配准则。设某传声器组有N（N≥3）个传声器，所有信号经EMD分解后，所得I MF分量维数D＝I MF分量进行降噪处理，舍弃其余信号。

将相邻传声器的对应层I MF函数进行互相关，求取时延值，那么在第l层所有I MF函数引起的时延误差为：

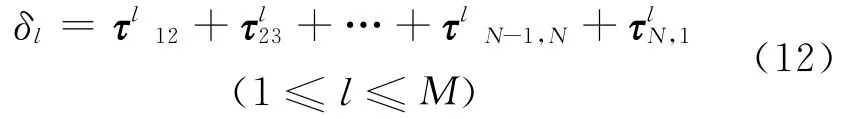
式（12）中，下标的数字表示传声器的标号。

M层I MF分量的时延误差可以构成矢量运算误差矩阵δ，如式（13）所示：

真实声信号传播到传声器阵列，信号时延差应满足时延矢量封闭准则，而噪声是环境中一直存在的，其满足矢量封闭法则的概率很低，几乎为0，因此δ矩阵反映了多尺度分解后多传声器信号在不同尺度上信号相关性的强度。在试验以前，对所用传声器分别进行性能评估，给出多传声器综合支持度λ＝ ［λ1，λ2，…，λN］。结合多传声器综合支持度，定义每一I MF尺度上的阈值为θ，则

定义每一层I MF权重为

由此可得，I MF分量对应的权重矩阵为：

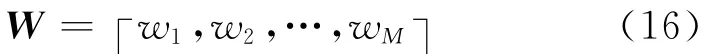
由此可见，满足时延矢量封闭准则的信号应为目标发出的信号，而权重为零的I MF成分通常为噪声成分。将分解得到的多尺度信号乘以相应的权重，采用下式对其进行重构，即得到真实估计信号，

此算法的程序流程图如图4所示。

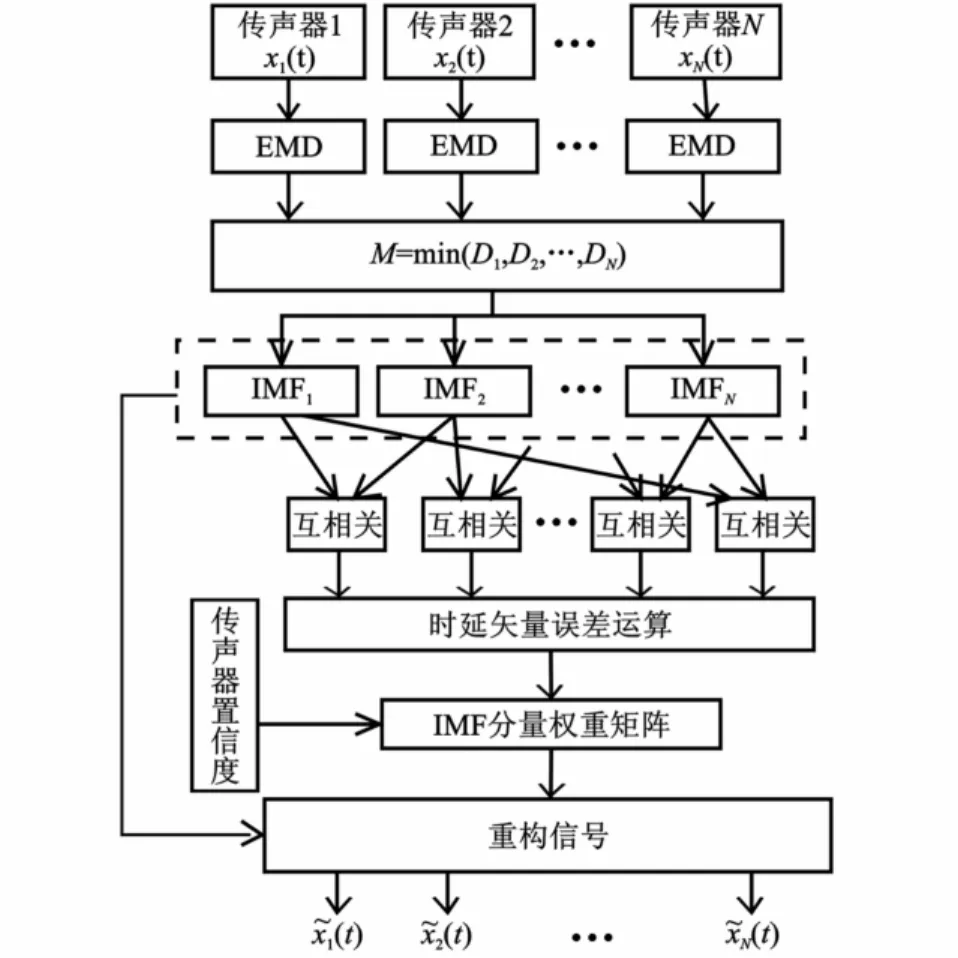
图4 程序流程图Fig.4 The flow chart of the algorith m

3 试验分析

3.1 试验仪器布置

使用传声器组对信号进行采集，要避免所有传声器处于同一波阵面上，声纳与雷达系统常采用均匀线阵。本文采用的传声器组布置成正四方形结构，如图5所示，将带有椭圆量角器的传声器标号定为1＃，逆时针旋转依次获得2＃、3＃、4＃传声器。

图5 传声器布置结构图Fig.5 The square construction of acoustic sensors

3.2 试验信号降噪处理

试验过程选择了两种目标的声信号，将试验所得信号按照图4所示的程序流程图，对信号进行降噪处理，结果如图6—图8所示。其中图6为四个传声器原始信号，图7、图8为程序运行后得到的四个传声器降噪信号，图中左侧的数字1、2、3、4分别表示1＃、2＃、3＃、4＃传声器，本文提出的算法在图中简化表示为EMD-TDVCR。由于传声器本身性能的差异，传声器综合支持度不同，采集所得信号的信噪比也不一样。由图6可知，支持度高的传声器（2＃）采集所得信号信噪比较高，支持度较低的传声器（4＃）采集所得信号信噪比较低。经过本文所提出的方法进行降噪处理后，四个传声器的信号均得到改善，高支持度的传声器信号真实性得以保持，而低支持度的传声器信号得到较大改善，充分体现了信息融合技术的优越性，如图7（b）、图8（b）所示。由于传声器的布局为正四方形，同时对信号源进行信号采集，各个传声器之间有一定的时延差存在，这一点在滤波后的信号中体现的更为明显。

图6 两种目标的原始含噪信号Fig.6 The noisy signals of t wo kinds of acoustic tar gets

图7 两种降噪方法处理后的目标1的信号图Fig.7 The denoised signals of tar get 1 by EMD-CMSE and EMD-TDVCR

试验将本文的算法与文献［3］所提出的EMD降噪算法（简化为EMD-CMSE）进行比较。图7（a）、图8（a）为文献［3］所提出的 EMD降噪算法的信号降噪结果。其中，图7 EMD-CMSE方法的信号降噪效果明显可以看出：传声器1的信号有着某种程度的失真，不利于后续信号处理。

表1列出了两种方法所得信号信噪比，从原始信号波形可以看出：传声器2的支持度较高，两种信号消噪技术得到的信噪比也是传声器2的最高，与试验条件相吻合。可见，本文所提出的方法信噪比较高，尤其对于传声器本身的性能缺陷，给予补充和完善，为后续信号使用奠定了良好的基础。

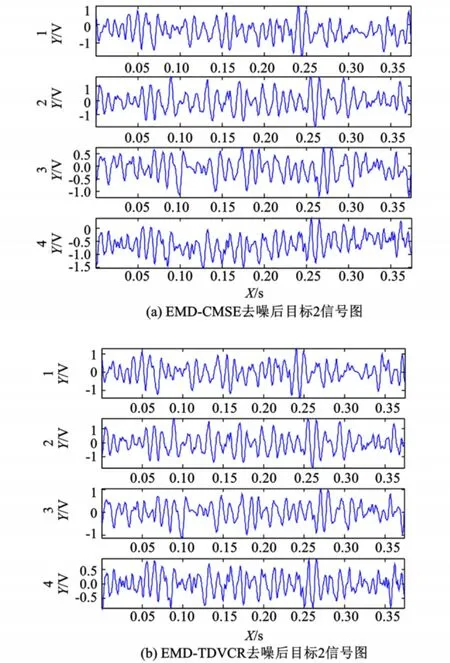
图8 两种降噪方法处理后的目标2的信号图Fig.8 The denoised signals of tar get 2 by EMD-CMSE and EMD-TDVCR

表1 两种算法的降噪效果比较Tab.1 The co mparison of SNRs of signals denoised by EMD-CMSE and EMD-TDVCR d B

4 结论

本文提出一种基于EMD和时延矢量封闭准则（TDVCR）的多传声器信号降噪算法。该方法首先将采集得到的信号进行EMD分解，将所得的对应I MF分量进行互相关，求取时延值，然后依据TDVCR进行时延矢量误差运算，得到I MF分量权重矩阵，最后根据I MFs及其对应的权重矩阵进行信号重构，得到去噪后的信号。试验表明：文中提出的方法有效利用了多传声器时延矢量匹配准则，不需要信号的先验知识，也不需要确定传声器之间的距离，避免了传声器位置对试验结果造成的误差，在不增加任何先验信息的前提下降低了噪声，取得了满意的试验效果，可应用于空旷无人区域或人类不易生存的地方，避免人力、物力的浪费。但算法的计算量相对较大，如何在保证算法有效性的条件下，降低运算复杂度是今后的一个研究方向。

［1］Zhang F，Tao R，Wang Y.Multi-channel sampling theorems f or band-limited signals with fractional Fourier transfor m［J］.Sci China Tech Sci，2008，51（6）：790-802.

［2］Norden E Huang，Zheng Shen，Steven R.Long.The empirical mode decomposition and the Hilbert spectrum f or nonlinear and non-stationary ti me series analysis［J］.Proceedings of the Royal Society，London，1998，454：903-995.

［3］Boudraa A O，Cenxus J C，Saidi Z.EMD-based signal noise reduction［J］.Inter national Jour nal of Signal Processing，2004，1（1）：33-37.

［4］Boudraa A O，Cenxus J C.EMD-based signal filtering［J］.IEEE Transactions on Instr u mentation and Measurement，2007，56（6）：2 196-2 202 .

［5］Lv Yanxin，Gu Xiaohui.An adaptive noise cancelling method based on EMD for acoustic in battlefield［J］.CISP，Tianjin，2009，8：4 053-4 056.

［6］王春，彭东林.Hilbert-Huang变换及其在去噪方面的应用［J］.仪器仪表学报，2004，25（52）：42-45.WANG Chun，PENG Donglin.The Hilbert-Huang transfor m and its application on signal denoising［J］.Chinese Jour nal of scientific Instr u ment，2004，25（52）：42-45.

［7］Weng B，Barner K E.Optimal and Bidirectional Opti mal empirical mode deco mposition［J］.ICASSP，2007，3：1 501-1 504.

［8］Looney D，Mandic D P.A Machine Lear ning Enhanced Empirical Mode Deco mposition［J］.ICASSP，2008：1 897-1 900.

［9］Kopsinis Y，Mc Langhlin S.Develop ment of EMD-based denoising methods inspired by Wavelet Thresholding［J］.IEEE Transactions on Signal Pr ocessing，2009，57（4）：1 351-1 362.

［10］Flandrin P，Rilling G，Goncalves P.Empirical mode decomposition as a filter bank［J］.IEEE Signal Process Letters，2004，11：112-114.

［11］Flandrin P，Rilling G，Goncalves P.EMD equivalent filter banks，from interpretation to applications，in Hilbert-Huang Transfor m and Its Applications［M］.Singapore：World Scientific，2005.

［12］Wu Z，Huang N E.A study of the characteristic of white noise using t he empirical mode decomposition method［J］.Proceedings of the Royal Society，London，2004，460：1 597-1 611.

［13］Huang N E，Wu Z.Statistical significance test of intrinsic mode f unctions，in Hilbert-Huang Transfor m and Its Applications［M］.Singapore：World Scientific，2005.