用海面磁偶极子源定位海底矢量磁传感器

杨明明，刘大明，连丽婷，张朝阳

（海军工程大学电气与信息工程学院电磁系，湖北 武汉 430033）

0 引言

舰船定位是实施舰船磁场检测、进而评估舰船磁性状态的首要步骤［1］。目前主要的定位方式可以分为以下两类：1）间接定位——在预知传感器与某固定参考点的相对位置后，再借助其他辅助设备（如DGPS［2］等）确定舰船与该参考点的相对位置，由此可以推算传感器与舰船的相对位置；2）磁定位——将舰船磁场用若干个磁源来等效，由测量数据反演磁源的磁矩和运动轨迹，从而确定各采样时刻传感器与目标的相对位置［3－8］。从上面的分析不难发现，无论采用何种定位方式，都需要预知传感器位置的先验知识：磁定位为传感器之间的相对位置，而间接定位为传感器与某参考点的相对位置。

文献［9］将舰船磁场等效为单个磁极子产生的磁场，在磁矩和传感器离水面的垂直距离已知的基础上，由磁场测量值和水深值来确定传感器与偶极子的相对位置的水平分量，即实现了传感器定位。然而，若无法准确获取磁矩，则该方法的定位效果急剧变差，而对磁矩实施精准测量是非常困难的。因此，本文提出采用位于海面的圆形载流线圈作为磁偶极子源来确定海底矢量磁传感器位置的方法。

1 传感器定位原理和优化算法

如图1所示，I为位于海面的圆形载流线圈，线圈半径为R，线圈匝数为N，电流为I，矢量传感器P位于海底。对传感器P进行定位的任务就是由传感器的磁场测量值来确定传感器自身相对于线圈中心的相对位置（xP，yP，zP）。在实际使用中，为了监测舰船磁场检测过程中水深的变化，一般在磁传感器上加装水深传感器，所以传感器离水面的垂直距离zP是可以利用的已知条件，因此定位的任务只需要确定传感器与磁偶极子相对位置的水平分量（xP，yP）。

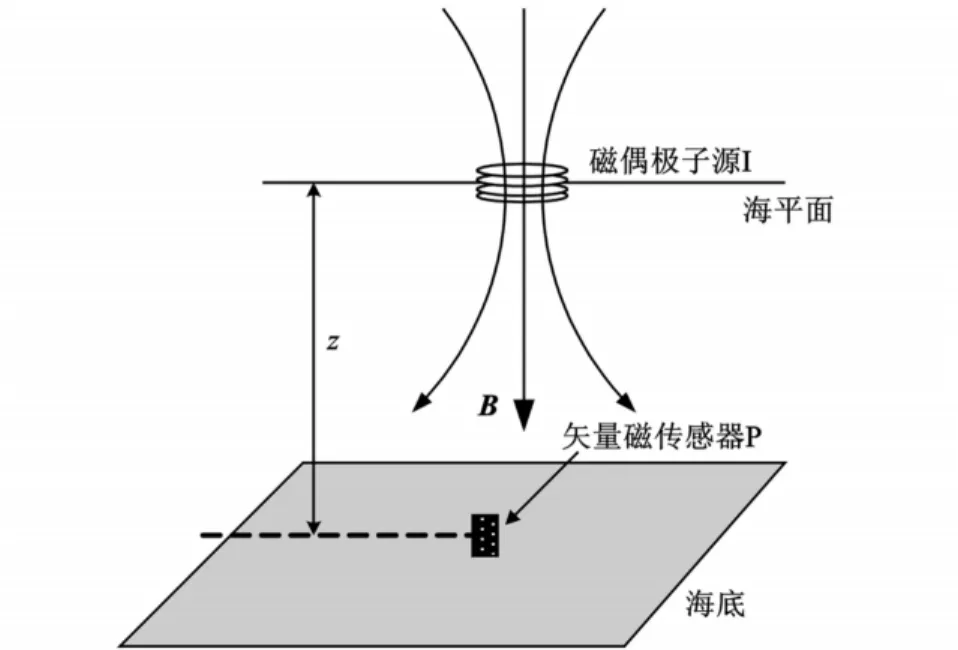
图1 海底矢量磁传感器的定位原理图Fig.1 Localization schematic of the undersea vector magnetic sensor

以线圈圆心为原点O′，x′和y′轴沿半径分别指向地磁北和地磁东，建立的右手坐标系称磁源坐标系O′-x′y′z′，见图2。磁源坐标系下，线圈所围范围外的任意场点r（xPyP，zP）处的磁感应强度为［10］：

式（1）中，rs为源点矢径，n为面S与线圈电流成右手螺旋关系的法线方向，B为磁感应强度，μ为介质的磁导率。

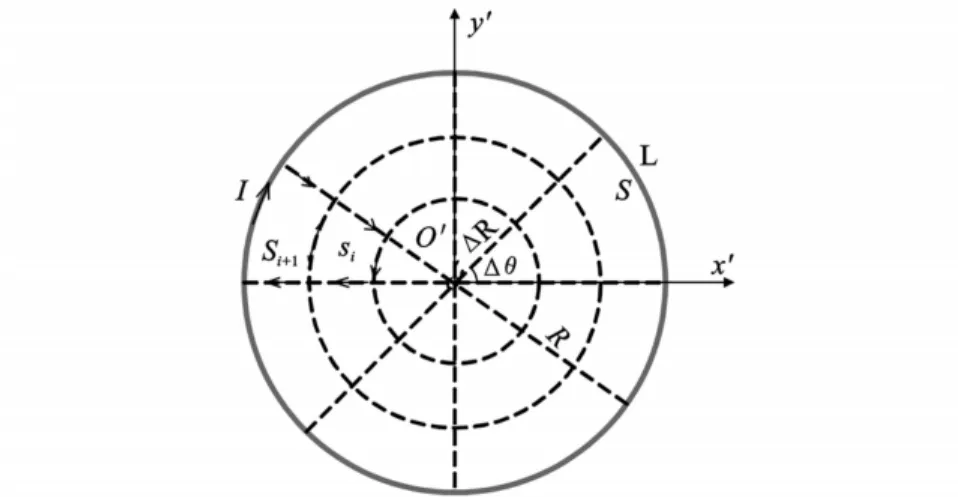
图2 磁偶极子源模型Fig.2 magnetic dipole source model

采用海面磁偶极子源定位海底矢量传感器的基本原理为：在场点r处测量得到线圈通电后产生的磁场，由式（1）计算传感器与磁源的相对坐标，实现传感器定位。

由传感器定位的原理，不难看出传感器定位本质就是从R2空间中寻找一个合适的位置矢量（xP，yP），使得从该矢量由式（1）正向推演的磁感强度（B）有效拟合测量值（Bc），属于无约束非线性规划问题。适用求解该问题的方法有步长加速法、Powell法［3，8］、Gauss-Newton法和 Levenberg-Marquardt（L-M）算法［11－12］等。L-M 算法能克服雅可比矩阵非满秩时，其他算法不稳定的困难，适合本问题的求解。因此本文选用L-M算法来求解位置矢量。

2 传感器定位方法

由上节的分析，可以发现：传感器定位方法的难点在于：如何计算线圈磁感应强度以及采用何种优化算法来求解位置参数，下面对其进行分别阐述。

2.1 磁感应强度的计算

由积分中值定理，式（1）可以化为：

式（2）中，re为面S内的矢径，me＝IS ne为等效磁矩，ne为该点处的法线，S为线圈所围面积。分析式（2）可以知道，当线圈尺寸远远小于源点到场点的距离时（至少15倍），则re的影响可以忽略，此时载流线圈的磁效应可以用位于线圈中心的单个磁偶极子来等效。如直接采用式（2）来定位传感器，则要求线圈半径R较小，考虑到实际使用时尽量增大电流和增加线圈匝数，磁源等效磁矩仍太小，造成传感器接收到的磁感应强度是一个非常弱的信号（几十纳特，甚至几纳特），这对传感器的探测能力（分辨率、精度和稳定度）和环境噪声都提出了较高的要求。

由于等效磁矩是随线圈尺寸的二次方变化，因此适当增大线圈尺寸能够较大幅度地增大等效磁矩。考虑到此种情况，本文采用如下的计算方法：将线圈所围区域S划分为N个单元，且对每个单元保证场点距该单元中心的距离远远大于单元的线度（具体的划分规则如图2，其中ΔR ≤zP／15，RΔθ≤zP／15），则载流线圈的磁感应强度为N个磁偶极子的磁感应强度的矢量和：

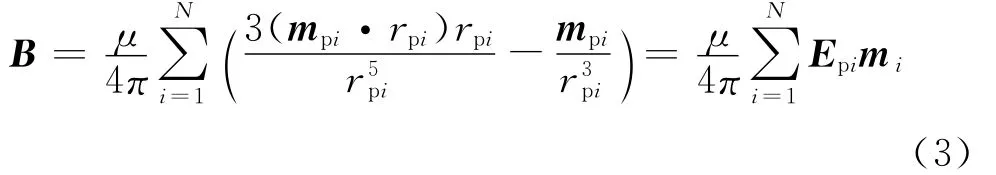
式（3）中，mi＝ISini为第i个单元等效磁矩；rpi为第i个单元中心到场点的矢径，其模为rpi。写成矩阵的形式为：

式（4）中，M ＝ ［（m1）T，（m2）T，…，（mN）T］T为等效磁矩向量，Bc为地磁坐标系下的磁场测量值，E＝（Ep1，Ep2，…，EpN）为联系等效磁矩与磁场测量值的观测矩阵。

2.2 L-M算法求解位置参数

在选择了合适的磁场计算方法后，实现传感器定位的关键在于如何计算传感器位置。从上面的分析，采用L-M算法求解位置参数具有较明显的优势，因此本文选用L-M算法来求解位置矢量。而采用L-M算法求解位置的难点在于，确定合适的目标函数和迭代初始点，为此本文提出如下的确定方法。

2.2.1 目标函数

传感器在观测磁偶极子源磁感应强度的过程中，不可避免地会引入测量误差，对于同一矢量传感器的不同分量，误差水平往往是不一样的。如果直接求解式（4）的非线性最小二乘解（L MS），则没有区分不同分量的测量误差对拟合的影响。在某个分量测量误差较大的情况下，可能出现对该分量的过度拟合，依此推算的位置也会出现偏差。因此本文采用加权最小二乘法（WL MS）来求解位置参数，对误差较大的分量给予较小的权值，对误差较小的分量给予较大的权值，目标函数为：

式（5）中，ΣB为测量系统的测量误差协方差阵，可以在线圈通电前对地磁场进行观测后计算得到。

2.2.2 迭代初始点

合适的初始迭代点不但能够保证从初始点出发稳定地收敛到全局最优解，而且可以有效减少迭代次数，缩短运行时间。由于磁矩都沿z轴方向（实际情况下，可以近似认为磁矩都沿z轴方向），下面分几种情况来确定迭代初始点（xp0，yp0）：

从式（6）和式（7）可以看出：如果磁矩沿z轴方向，测量误差是乘性噪声且各分量的信噪比一致，则迭代初始点与真解的距离不会超过线圈半径。在确定了目标函数和迭代初始点后，我们就可以利用LM算法来求解传感器位置，有关L-M算法的实现可以参考文献［12］，这里不再赘述。

综上所述，传感器定位方法的主要步骤为：在线圈接通电源之前，首先多次采样地磁背景，确定测量误差协方差阵ΣB；其次由水深测量值将载流线圈划分为N个单元，计算N个等效磁偶极子的位置，并根据线圈匝数和线圈电流确定各磁偶极子的等效磁矩；再次由传感器输出值（磁场测量值）确定迭代初始点；最后由该迭代初始点出发采用L-M算法计算传感器位置，完成自身定位。

3 模型实验验证和定位影响因素仿真

3.1 模型实验

如图3，磁偶极子源参数：线圈共计50匝，线圈半径R＝0.07 m，线圈电流I＝3 A。在磁偶极子源的下方共布设9个矢量磁传感器，测量平面距磁源中心的高度为0.59 m；地磁坐标系下9个传感器的坐 标 场 点 为：p1（0.4，0.4，0.59），p2（0，0.4，0.59），p3（－0.4，0.4，0.5 9），p4（0.4，0，0.5 9），p5（0，0，0.59），p6（－0.4，0，0.59），p7（0.4，－0.4，0.59），p8（0，－0.4，0.59），p9（－0.4，－0.4，0.59）。

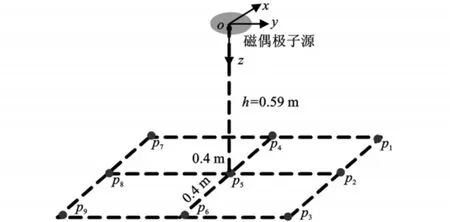
图3 模型实验示意图Fig.3 Schematic diagram of model experi ment

实验的主要步骤为：1）线圈接通电源前，测量系统以采样周期T＝1 s采集地球磁场，共获得的地磁样本为100×9组数据（传感器数据点个数×传感器个数）；2）对每个传感器，以这100个数据点的均值作为该传感器测量得到的地磁背景，并由此推算每个传感器坐标与地磁坐标的转换矩阵A1，估计每个传感器在传感器坐标下的协方差矩阵Σe，由此可以的磁场，减去地球磁场后再将其转换到地磁坐标系记为Bc；4）利用上面介绍的方法定位每个传感器的位置（zp为已知量）。

图4给出了9个传感器的实际位置、迭代初始点和定位结果。从图中可以看出：迭代初始点靠近传感器实际位置，说明迭代初始点的挑选方法是合适的；计算得到的位置与实际位置差别较小，验证了定位方法的有效性。定义定位的相对误差Re：

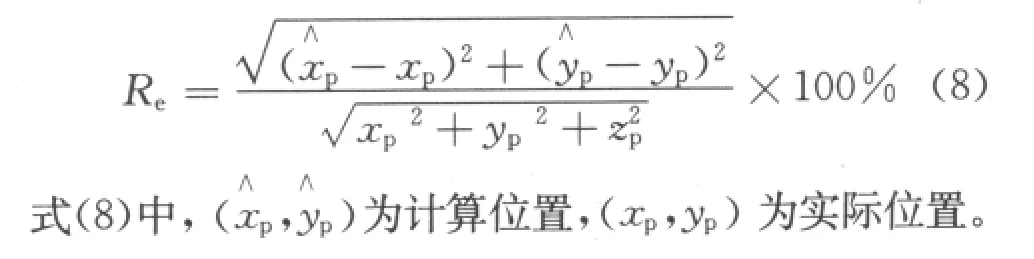
图4 9个传感器的定位结果Fig.4 Localization results of 9 sensors

表1给出了选用不同目标函数对应的定位误差。从表中可以看出：在本次实验中，不管采用最小二乘或是加权最小二乘法作为目标函数来求解传感器位置都具有较高的精度（相对误差不大于4%）；加权最小二乘的定位结果略好于最小二乘法的定位结果，但是误差分布并没有充分反映加权最小二乘法的优势，主要原因是模型实验采用的测磁系统的精度较高，传感器各分量的误差水平相当（方差都在10 n T附近），有理由相信实际使用中加权最小二乘法可有效处理各分量误差水平差别较大的情形。

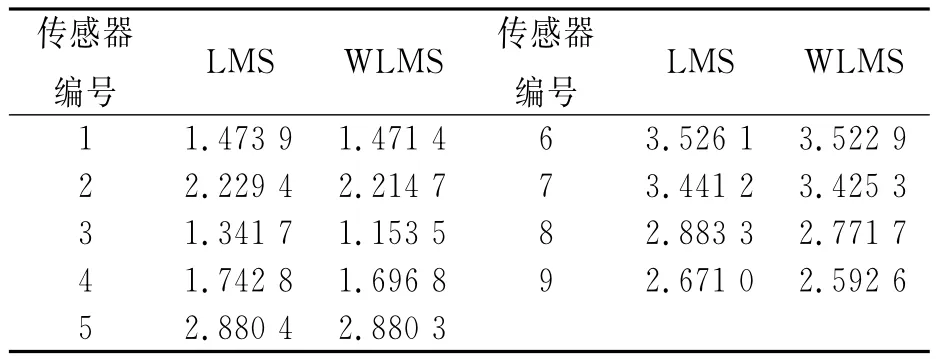
表1 定位相对误差表Tab.1 localization relative error %

3.2 定位影响因素仿真分析

将本文中的方法应用于实际，则应当考虑磁偶极子源的布置问题。圆形导航浮标在移动磁性检测站的投放、维护、指引舰船正确通过和数据传递中发挥着广泛的作用［1］。如果在浮标上安装线圈和适当的电源，就可以构成磁偶极子源，也就可以将本文中的方法应用于实际。由于浮标锚泊在海上，容易受到风、浪、涌、流等海洋环境载荷的作用，会产生六个自由度的摇荡运动，即横摇、纵摇、平摇、纵漂、横漂和升沉运动［13］。由于平摇、纵漂和横漂不具有恢复力，多通过锚泊系统来对其约束；并且各个传感器的采样时刻是同步的，所以这三种运动对定位结果的影响影响可以不必考虑。而水深的变化可以由水深传感器测量得到，则升沉运动的影响也可以忽略。对于圆形浮标而言，横摇和纵摇可以视为同种形式的运动，它们作用的结果就是使得线圈平面偏离地磁坐标系的x Oy平面，即磁源坐标系与地磁坐标系不再重合，如图5所示。

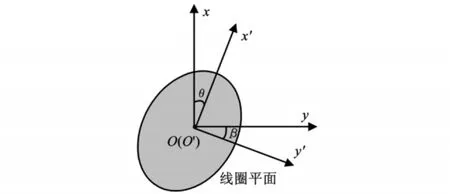
图5 磁源坐标系与地磁坐标系的关系Fig.5 geo magnetic and magnetic source coor dinates

本文对不同的θ和β仿真结果见表2，其中仿真参数设置为：R＝2 m，I＝5 A，n＝50匝；选取三个场点p1（0，0，20），p2（10，10，20）和p3（－10，10，20）作为考核点；三个场点的磁场计算值叠加20 d B的随机噪声后作为磁场测量值；利用本文介绍的方法求解考核点的位置，按式（8）计算这三个场点的均方根误差作为考核误差。

表2 不同的θ和β对应的误差分布Tab.2 Error distribution of differentθandβ

从表中可以看出，当θ和β小于5°时，定位的误差可以控制在5%以内。同时本文还采用上节的模型对纵摇和横摇的影响进行了实验，当θ＝β＝7°时，9个传感器的最大定位误差为5.777 3%。

4 结论

本文提出了一种利用海面的磁偶极子源来定位海底传感器的方法。在确定合适的磁源参数（线圈半径、电流和线圈匝数）后，传感器定位方法的主要步骤为：在线圈接通电源之前，首先多次采样地磁背景，确定测量误差协方差阵ΣB；其次由水深测量值将载流线圈划分为N个单元，计算N个等效磁偶极子的位置，并根据磁源参数确定各磁偶极子的等效磁矩；再次由传感器输出值（磁场测量值）确定迭代初始点；最后由该迭代初始点出发采用L-M算法计算传感器位置，完成自身定位。从模型实验和仿真分析可以看出：采用L-M算法确定海底传感器位置具有较高的精度，当风浪引起线圈平面与地磁坐标系的偏转角小于5°时，该方法仍然可以用于对海底传感器的定位。在实际中检验该方法，将θ和β视为参变量利用多个传感器的数据同时实现传感器定位和角度观测是下一步要研究的重点。

［1］John S Kay.Equip ment develop ment for t he measurement of under water multi-influence fields［J］.IPENZ Transactions，1997，24（1）：48-60.

［2］江南，孙少华.DGPS技术在水中兵器试验中的应用研究［J］.昆明理工大学学报（理工版），2003，28（1）：67-69.JIANG Nan，SUN Shaohua.Applicative study on DGPS technology in under water weapon test［J］.Journal of Kunming University of Science and Technology（Science and Technology），2003，28（1）：67-69.

［3］林春生，龚沈光.舰船物理场［M］.北京：兵器工业出版社，2007.

［4］林春生.舰船磁场信号检测与磁性目标定位［D］.武汉：海军工程学院，1996.

［5］胡海滨.磁性目标探测与定位研究［D］.武汉：海军工程大学，2003.

［6］胡海滨，林春生，龚沈光.基于母函数正交化的模型化磁性物体矢量探测和定位［J］.探测与控制学报，2006，28（3）：5-8.HU Haibin，LIN Chunsheng，GONG Shenguang.A modelization method of magnetic object detection and localization based on ort hogonalization mother f unctions［J］.Journal of Detection ＆ Control，2006，28（3）：5-8.

［7］隗燕琳，肖昌汉.基于舰船矢量磁场的定位方法［J］.上海交通大学学报，2009，43（8）：1 216-1 221.WEI Yanlin，XIAO Changhan.A new magnetic localization method based on vessel＇s vectorial magnetic field［J］.Jour nal of Shanghai Jiaotong University，2009，43（8）：1 216-1 221.

［8］蒋敏志，林春生.船舶水下被动磁定位研究［J］.武汉理工大学学报（信息与管理工程），2003，25（6）：168-170.JIANG Minzhi，LIN Chunsheng.Research on vessel location by under water passive magnetic signature［J］.Jour nal of Wuhan University of Technology（inf or mation ＆ management engineering），2003，25（6）：168-170.

［9］Jonas Call mer，Martin Skoglund，Fredrik Gustafsson.Silent localization of under water sensors using magneto meters［J］.Eurasip Jour nal on Advances in signal pr ocessing，2009：1-8.

［10］冯慈璋，马西奎.工程电磁场导论［M］.北京：高等教育出版社，2009.

［11］Hu Chao，Meng Max Qinghu，Mandal Mrinal.Efficient magnetic localization and orientation technique for capsule endoscopy［C］／／ Engineering in Medicine and Biology 27thAnnual Conference，Shanghai：IEEE，2005：7 143-7 146.

［12］袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2001.

［13］任贵永，孟玿瑛.海洋大型导航浮标研究［J］.海洋学报，1993，14（4）：114-121.REN Guiyong，MENG Zhaoying.Study of Large-scale marine navigation buoys［J］.Acta Oceanologica Sinica，1993，14（4）：114-121.