基于蚁群优化的异步电机矢量控制系统的研究

苏宏立 黄铭芝 朱向华 应 涛

（中国联合工程公司，浙江 杭州 310022）

1 问题的提出

异步电动机矢量控制是基于电动机动态数学模型，较好地解决了电动机定子三相电流转矩分量和励磁分量的耦合问题，大大提高了异步电机变压变频调速系统的动态性能，在现实生活中应用比较广泛。

电动机在实际运行过程中，由于温度升高、频率变化、磁路饱和等因素的影响，电机参数会偏离初始设定值。而电动机矢量控制是建立在动态数学模型基础之上，对电机参数具有很强的依赖性，特别是转子时间常数的变化对矢量控制系统影响最大。

针对上述问题，前人研究了基于人工神经网络、基于模糊PID等一些观测参数优化控制器的自适应控制方法，这些方法在实际中起到了较好的效果。但是这些方法有些结构复杂，有些需要较多的先验知识，更主要的是在调速性能要求较高的场合，这些方法的在线实时性并不理想。

本文通过Hammerstein模型及最小二乘在线辨识技术，辨识出变化后的系统模型参数，然后采用蚁群优化算法在线调节控制器参数，精度较高，实时性较好，得到了不错的仿真效果。你要给我的：480*2（住宿）+47*4+24（车票）+238（鞋子）+94（裤子）+30*4+15（索道）=1639

2 非线性系统最小二乘在线辨识

最小二乘辨识方法是一种简单、实用、易于在线实现的系统辨识方法。实际工程中有广泛应用。而辨识对象——异步电机矢量控制系统是一个耦合紧、阶次高、非线性强、参数时变的系统。对这样一个系统的在线辨识，是相当复杂的。本文采用的是哈默斯坦模型。

哈默斯坦模型（如图1）是用一个无记忆非线性增益和一个线性子系统描述一个非线性系统的模型。

图1 哈默斯坦模型结构

无记忆非线性增益也可以是其他形式，在这里选用的是指数函数。

可以把上述模型转换为最小二乘一般式，

对于上述模型可以采用递推最小二乘法估计出模型参数。在辨识出θ赞后，可令r1=1，再次使用最小二乘法估计ri,i=2,…,m。

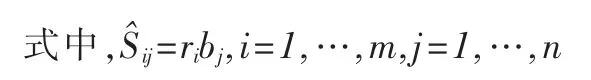
3 蚁群算法优化PID控制器

蚁群算法是受自然界中真实蚂蚁觅食的群体行为得到启发而提出的，其很多观点都来源于真实蚁群。自1991年意大利学者Dorigo M等在法国巴黎召开的第一届欧洲人工生命会议上第一次提出蚁群算法的基本模型以来，蚁群算法已经在TSP问题、车辆路径问题、车间作业调度问题，以及电力系统、机器人领域、数据挖掘、聚类分析、参数辨识、控制参数优化等多个领域得到广泛应用，并取得了相当丰富的研究成果。

PID控制在20世纪30年代就已经提出，由于其算法简单，使用方便，鲁棒性好，可靠性高等优点，目前在工业控制领域仍有广泛应用。因此PID参数的整定与优化，特别是在对象参数发生变化，对象模型发生改变时，就显得尤为重要。目前除了传统的经验法和Z-N法，很多仿生优化算法也在PID参数优化方面有很好的效果，这里介绍的是蚁群算法在PID控制中的参数优化。

3.1 蚁群算法基本思想

蚁群算法来源于蚁群在寻找食物过程中能找到最短路径的现象。蚂蚁并没有视觉，但是行进中会通过在路径上释放出一种特殊的分泌物——信息素来分辨路径。当它们碰到一个从未走过的路口时，会随机的挑选一条路径前行，同时释放出与路径长度相关的信息素。蚂蚁所走的路径越长，所释放的信息素就越少。当后来的蚂蚁也来到这个路口时，会选择信息量更大的路径的概率相对较大，这样便形成一个正反馈机制。最优路径上的信息量越来越大，而其他路径上的信息量会随时间逐渐减少消逝，最终蚁群就可以找到最优觅食路径。

3.2 蚁群算法优化PID参数

蚁群算法最早应用于旅行商问题（TSP）。将其应用到控制器参数优化领域中时需要做一些调整。

（1）设置路径节点。用蚁群算法优化PID控制参数，首先，需要确定PID参数的取值空间，以避免在整个空间域上寻优导致收敛过于缓慢。可以采用传统Z-N法整定的K*p,K*i,K*d,为中心，进行扩展，得到可行解空间。其数学表式达如下：

其中，0燮λ，ε燮1。

然后把此可行解空间离散化，作为蚂蚁路径的节点（如图 2）。

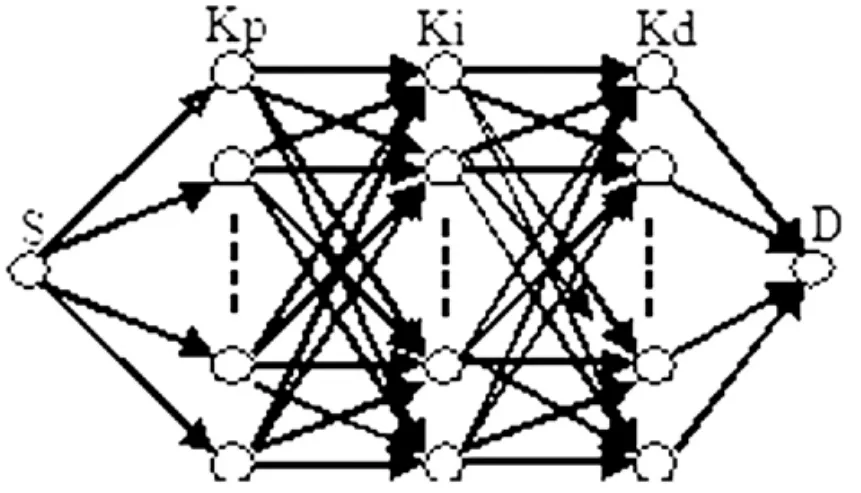
图2 PID路径节点示意图

（2）确定转移概率。蚁群从一个节点出发，向下一层节点群前进，但是每只蚂蚁只能选择其中的一个节点，具体选择哪一个节点，有随机因素的影响，但更主要的是转移概率。

第k只蚂蚁从节点i转移到节点j的概率是，

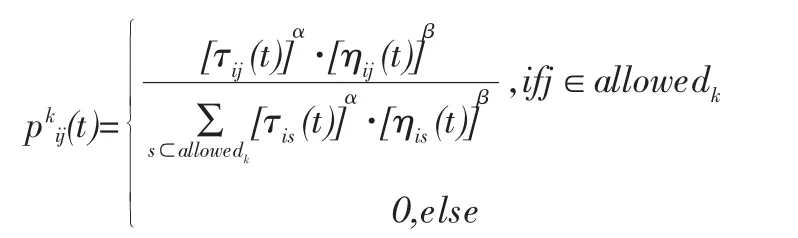
其中，τij(t)表示某时刻t从i节点到j节点的信息素，

ηij(t)表示某时刻t从i节点到j节点的能见度，

α表示轨迹的相对重要性，

β表示能见度的相对重要性。

（3）计算目标函数。每只蚂蚁完成一条PID路径选择之后，需要计算出各自的目标函数值，以得到最优路径。目标函数的选择需要反映出系统最关注的性能指标信息。工程中通常选取绝对误差矩的积分作为指标。即：

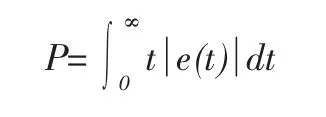
离散化后，

其中Ts是仿真步长，n是仿真点数。

（4）更新信息素。蚁群完成一次寻优后，需要更新每条路径的信息素。这其中包括两个方面，一是蚂蚁走过的路径信息素增强，一是蚂蚁未走路径信息素减弱。

t+n时刻路径（i，j）上的信息量可按如下规则调整，

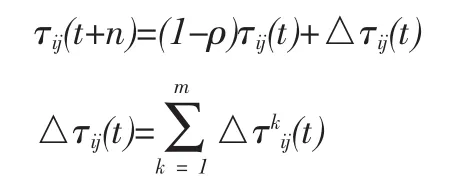
其中，ρ表示信息挥发系数，△τij(t)表示本次循环中路径（i，j）上的信息增量，△τkij(t)表示第 k 只蚂蚁本次循环中路径（i，j）上的信息增量。

信息素增量的更新，可按如下规则，式中，Q表示信息素强度，Lk表示第k只蚂蚁在本次循环中所走路径的目标函数值。

4 实验仿真

4.1 控制系统结构设计

本文结合异步电机矢量控制系统进行了参数时变，在线辨识，在线蚁群优化的仿真，控制系统结构如图3所示。

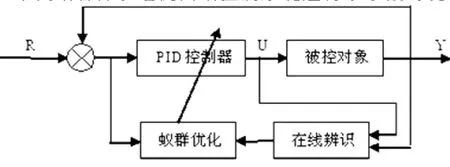
图3 控制系统结构框图

4.2 具体仿真设计

仿真中选用的电机 Pn=4KW，Un=400V，Fn=50Hz，Nn=1430r/m，Rs=1.405Ω，Rr=1.395Ω，Llr=Lls=0.005839H，Lm=0.1722H，J=0.0131kgm2，np=2。

仿真时间为 2s，初始 Kp=15，Ki=5，Kd=0.01。 在 0.5s时改变电机参数 Rs=2.0Ω，Rr=2.0Ω，Lm=0.2H，1s时使用蚁群算法优化 PID，优化后 Kp=35.7，Ki=5.15，Kd=0.001。Simulink系统结构如图4所示，仿真结果见图5，图6。

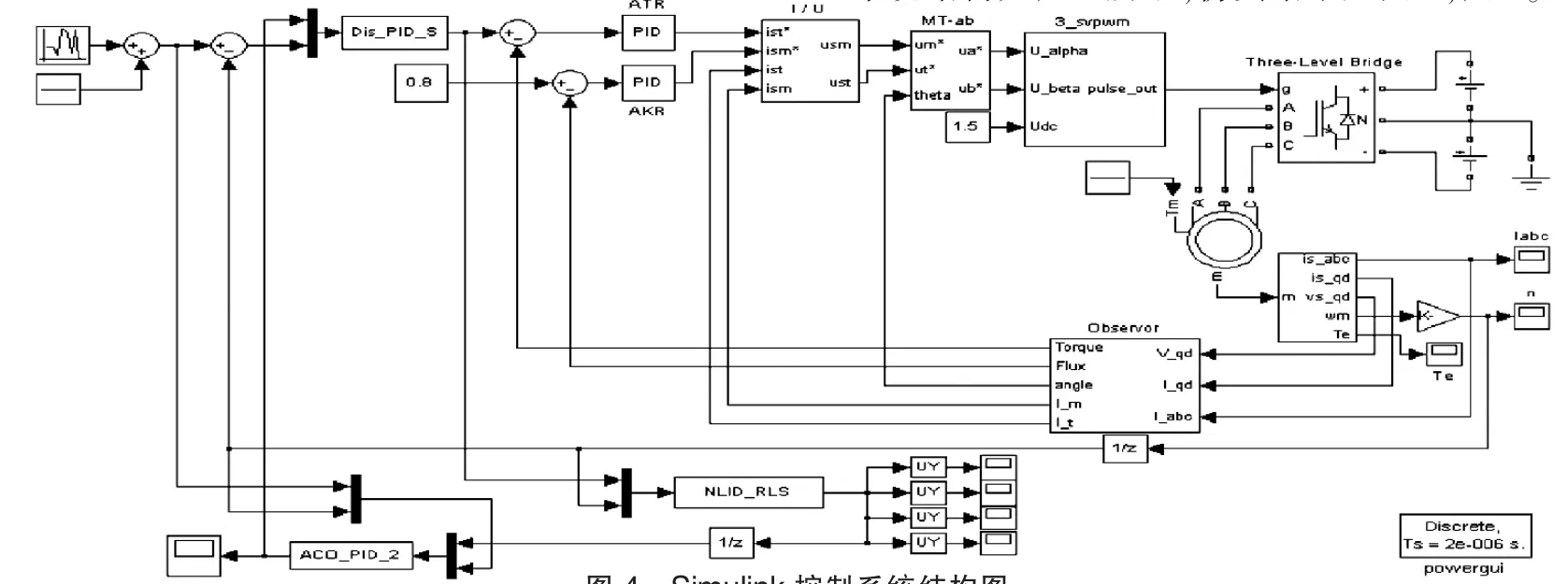
图4 Simulink控制系统结构图

可以看到在0.5s系统结构参数发生变化以后，控制系统的转速、电流都受到一定的影响，性能变差，1s时通过蚁群优化以后系统特性得到改善。

图5 转速仿真曲线

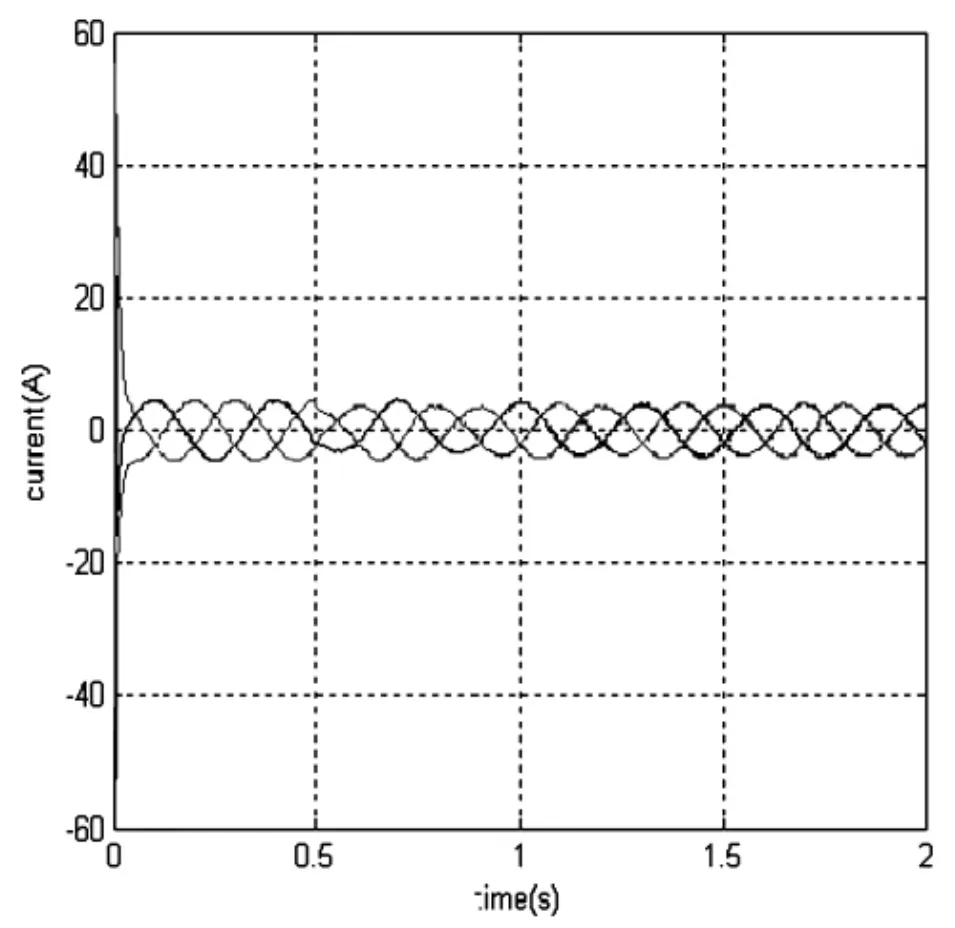
图6 电流仿真曲线

5 结论

理论分析和仿真研究表明，本文提出的方法是有效可行的。通过最小二乘非线性系统在线辨识和蚁群优化算法的结合，可以较好的抑制系统时变参数的影响。不仅可以满足异步电动机矢量控制的实时性要求，方法简单，易于编程实现，而且可以大大改善异步电动机的动态、稳态特性，提高了系统的自适应性与鲁棒性。

[1]李华德，尚德舜．电机参数变化对矢量控制系统的影响分析[C]．第二十二届中国控制会议论文集,2003.

[2]Besir Dandil．Fuzzy neural network IP controller for robust position control of induction motor drive[J]．Expert Systems with Applications，2009， (36)： 4528–4534.

[3]Raja S.Toqeer，N.Suha Bayindir．Speed estimation of an induction motor using Elman neural network[J]．Neurocomputing，2003， (55)：727–730.

[4]Feng Ding， Tongwen Chen． Identification of Hammerstein nonlinear ARMAX systems [J]．Automatica，2005， (41)：1479-1489.

[5]段海滨．蚁群算法原理及其应用[M]．北京：科学出版社,2005.

[6]夏天昌．系统辨识――最小二乘法[M]．北京：国防工业出版社．1984.

[7]S.I.Biagiola，J.L.Figueroa． Wiener and Hammerstein uncertain models identification [J]．Mathematics and Computers in Simulation，2009，(79)：3296–3313

[8]ER-WEI BAI．An Optimal Two-Stage Identification Algorithm for Hammerstein －Wiener Nonlinear Systems．Automatica，Vol.34，No.3，pp.333—338，1998

[9]马良，朱刚，宁爱兵．蚁群优化算法[M]．北京：科学出版社．2008.

[10]尹宏鹏，柴毅．基于蚁群算法的PID控制参数优化[J]．计算机工程与应用，2007，(17)：43.

[11]Duan Haibin，Wang Daobo，Yu Xiufen． Novel Approach to Nonlinear PID Parameter Optimization Using Ant Colony Optimization Algorithm[J]．Journal of Bionic Engineering，2006，(2).

[12]詹士昌，吴俊．基于蚁群算法的PID参数优化设计[J]．测控技术，2004，(1).