特高压输电塔脉动风场模拟分析

郭启波

0 引言

输电塔多为格构式塔线体系，与通常的结构风荷载作用模型不同，由于缺乏相应的观测资料和试验结论，还没有得到普遍认同的风荷载作用模型。格构式塔在风荷载作用下不仅发生顺风向振动，而在横风向也会发生相同量级的振动。实际上，格构式塔横风向动力风荷载的形成原因不是各个构件尾流中旋涡脱落的一种简单集合，而是来流穿绕格构式塔架时，各构件尾流相互干扰形成的某种较大尺度的尾流。由于目前条件的限制，现场实测的脉动风速时程信号非常有限，并且项目建成前所取得的短期风速记录资料未能考虑风速的空间相关性。用实测的风速时程进行风振分析有一定的局限性，利用谐波合成法进行人工风速时程的模拟能很好的解决这个问题。

1 三维空间脉动风场模拟

目前，国内外对脉动风速时程的模拟方法主要有三类。一类是利用三角函数叠加的谐波合成法(WAWS);第二类是基于数字滤波技术的线性滤波法，如自回归算法(AR)、移动平均算法(MA)及自回归移动平均算法(ARMA)等;第三类方法是利用小波在时域和频域上同时具有良好局部化特性，采用离散小波变换重构风速时程。

1.1 谐波合成法

考虑一个一维n变量的平稳高斯随机过程{fj(t)}(j=1，2，…，n)，其互相关函数矩阵为:

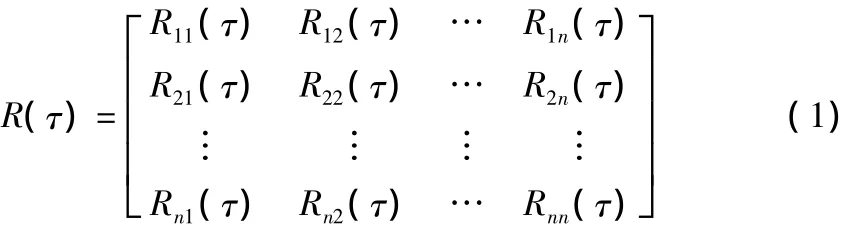
互谱密度矩阵为:

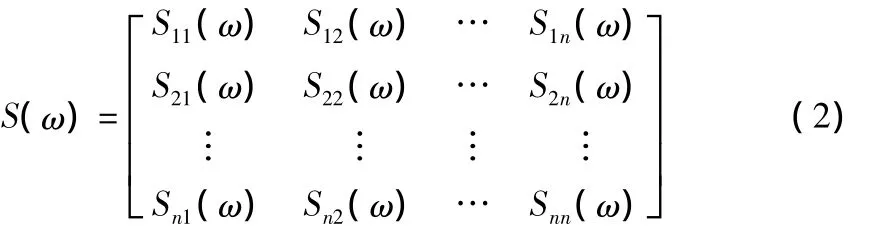
互相关函数矩阵的元素与互谱密度矩阵的元素存在如合维纳—辛钦(Wiener-Khintchine)关系式:

根据Shinozuka的理论，随机过程{fj(t)}的样本可由下式来模拟:

其中，N为采样频率点数，理论上应有N→∞，实际上N为一充分大的正整数即可保证模拟的精度，为了能在计算中使用FFT技术，一般N=2α，α为正整数;Δω=ωup/N为频率增量，ωup为上界截止频率，即当ω＞ωup时S(ω)=0，ωup可用下式估算:

其中，ε≪1，例如 ε =0.001;φml为均匀分布于[0，2π)区间的随机相位角;ωl为频率:

其中，δωl为均匀分布于(- Δω′/2，Δω′/2)的随机频率，Δω′≪Δω。δωl的引入是为了消除模拟随机过程的周期性，但它以牺牲效率为代价，因而Jeffrie建议最好不用随机频率措施;

Hjk(ωl)为S(ωl)的Cholesky分解矩阵H(ωl)中的元素，即:

由于理论上S(ωl)一般是复数矩阵，因此H(ωl)通常也是复数矩阵，其对角元素为实数，非对角元素为复数。HT*(ωl)为H(ωl)的共轭转置矩阵。矩阵H(ωl)的元素存在如下一些关系:

θjm(ωl)为 Hjm(ωl)的幅角:

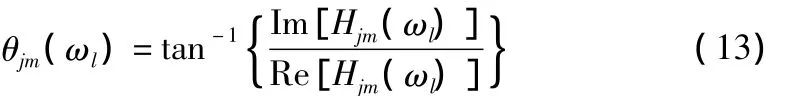
Im和Re分别表示取复数的实部和虚部。

为了避免模拟结果的失真现象，时间间隔Δt必须满足以下关系式:

由以上分析可知，只要知道随机过程{fj(t)}的互谱密度矩阵S(ω)，选择适当的采样频率点数N，上界截止频率ωup和采样时间间隔Δt，就可以模拟出随机过程的时间历程。

可以证明，式(5)模拟随机过程的均值为零，相关函数和功率谱密度随N→∞而收敛到目标相关函数和目标功率谱。

Gj(pΔt)由下式给出，可通过FFT进行计算:

其中，

计算过程中的目标功率谱为双边功率谱，而实际风工程常用的一般都是单边功率谱，在用以上方法进行脉动风速的模拟过程中要将目标功率谱转换为双边谱。

1.2 脉动风模拟实例

运用上节的谐波合成法，对某±800 kV特高压直流输电塔线体系进行了空间三维脉动风场模拟，主要参数见表1，衰减系数Cx，Cy，Cz分别取为 8，16，10。模拟点数为 61 个点，如图 1 所示。

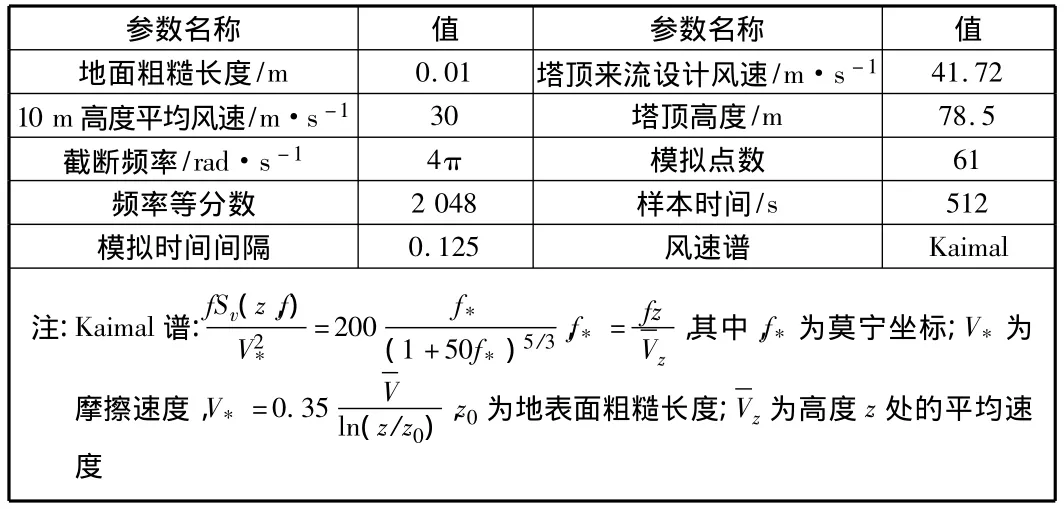
表1 模拟脉动风速时程的计算参数

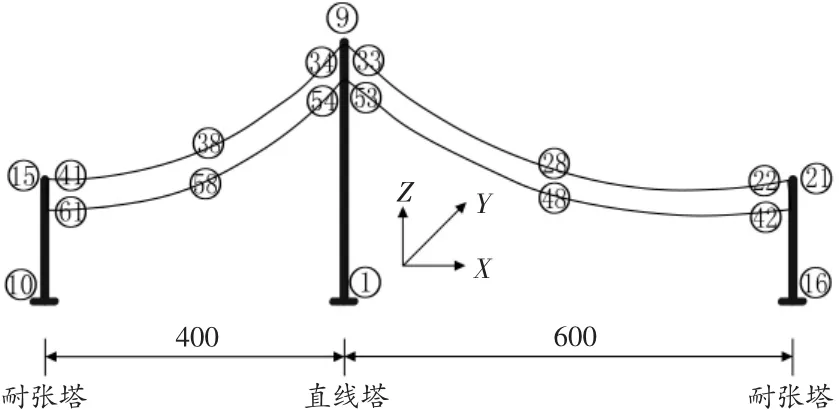
图1 塔线体系示意图

塔底和塔顶及中跨跨中点处三维脉动风速及功率谱密度如图2，图3所示。

图2 顺风向脉动风时程曲线

塔线体系中各点顺风向脉动风速时程曲线如图2所示。模拟数据的统计分析表明，其统计特征检验符合假定条件。

为了验证模拟方法的有效性和可靠性，对模拟风速场的功率谱与目标风速谱进行了检验，模拟点风速功率谱如图3所示。模拟风速功率谱的谱线趋势与目标谱线是一致的，其谱线的总体均值与目标谱也很接近。这表明，该方法能准确有效地模拟出符合要求的三维多变量随机样本。

图3 模拟风谱与目标谱的比较

2 结语

本文运用以谐波合成法为基础的脉动风速时程的模拟方法实现了对某±800 kV特高压直流输电塔线体系的脉动风的模拟，并通过模拟风速功率谱的谱线趋势与目标谱线进行对比，得到以下结论:

1)谐波合成法是一种精度较高且无条件稳定的随机过程模拟方法，运用谐波合成法，对输电塔线体系进行了顺风向脉动风场模拟。模拟数据的统计分析表明，其统计特征检验符合假定条件。

2)通过对模拟脉动风的功率谱与目标功率谱验证，该方法能准确有效的模拟出符合要求的随机变量。

[1]Battista R C，Rodrigues R S，Pfeil M S.Dynamic behavior and stability of transmission line towers under wind forces[J］.Journal of Wind Engineering and Industrial Aerodynamics，2003(91):1051-1067.

[2]Rao G V.Optimum designs for transmission line towers[J］.Computers ＆ Structures，1995，57(1):81-92.

[3]龚 靖，贾瑞庆.薄壁钢管输电塔架风载响应研究[J］.东北电力学院学报，1998，18(4):76-84.

[4]王世村，孙炳楠，楼文娟，等.单杆输电塔气弹模型风洞试验研究和理论分析[J］.浙江大学学报(工学版)，2005，39(1):87-91.

[5]付国宏，程志军，孙炳楠，等.架空输电线路风振试验研究[J］.流体力学实验与测量，2001，15(1):15-21.

[6]邓洪洲，朱松晔，王肇民.大跨越输电塔线体系动力特性及风振响应[J］.建筑结构，2004，34(7):25-28.

[7]邓洪洲，朱松晔，苏 速，等.大跨越输电塔线体系风振控制风洞试验[J］.同济大学学报，2003，31(9):1009-1013.

[8]邓洪洲，朱松晔，陈晓明，等.大跨越输电塔线体系气弹模型风洞试验[J］.同济大学学报，2003，31(2):132-137.

[9]卢文生，陈 亦.大跨越输电线体系风荷载模拟[J］.特种结构，2004，21(3):12-14.

[10]程志军.架空输电线路静动力特性及风振研究[D］.杭州:浙江大学，2006:4-7.

[11]王力争.输电塔风振系数简化计算[J］.中国电力，1998，31(10):16-18.

[12]Lou Wenjuan，Sun Bingnan，Tan Jinchun.Wind Tunnel Test and Numerical Computation on Wind-induced Vibration for Tall Lattice Tower[J］.Journal of Vibration Engineering，1996，9(3):318-322.

[13]李正良，肖正直，韩 枫，等.1 000 kV汉江大跨越特高压输电塔线体系气动弹性模型的设计与风洞试验[J］.电网技术，2008，32(12):1-5.