基于双门限盒维数与信息维数的协作感知方法

陈小波,陈 红,刘 佳,蔡晓霞

(1.解放军电子工程学院信息系,安徽合肥 230037;2.安徽大学计算智能与信号处理教育部重点实验室,安徽合肥 230039)

0 引言

超宽带(UWB)无线通信系统具有通信容量大、辐射功率密度低、抗多径干扰等优点,但它本身存在的频谱共享问题,必然会对其他无线通信系统造成干扰;认知无线电(cognitive radio,CR)技术的研究,为解决此问题提供了一种可行性方案[1]。频谱感知是CR的关键部分,认知用户通过频谱感知,“见缝插针”,切入频谱进行信号传输,有效地利用空闲频谱资源。频谱感知的方法主要有能量检测、匹配滤波器检测、循环谱特征检测等,这些方法各有其优缺点[2-4]。模拟授权用户攻击针对经典频谱感知技术的缺陷,通过模拟授权用户信号特征来发射信号,从而干扰频谱感知过程,由于超宽带系统划分政策中,频谱范围内各授权信号调制样式已知,为了减少甚至有可能性地避免频谱干扰,对调制样式进行识别有助于判断区分授权信号、干扰信号以及噪声。循环谱特征检测被视为最适合认知超宽带(cognitive ultra-wideband,CUWB)系统的频谱感知方法[5],该方法能够对信号调制样式进行识别,且能够获得比能量检测好的检测效果,但是该方法的运算复杂度高,需要较长的感知时间。

分形维数可以定量描述分形集的复杂性,通信信号作为一种时间序列,分形能对它进行有效地刻画,分形维数中的盒维数通常用来描述分形信号的信息度量,信息维数描述分形信号在平面空间上的分布信息,结合盒维数和信息维数以及CUWB的特点,本文提出一种基于双门限盒维数与信息维数的CUWB协作频谱感知方法。

1 分形维数检测基础

1.1 盒维数

盒维数用于描述分形信号的几何尺度信息,接收机对接收信号采样为{s(),s(t2),s(t3),…,s(tN),s(tN+1)},其中N取偶数,采样点共T=N+1点,根据盒维数的简化形式[6]:

盒维数Db定义为:

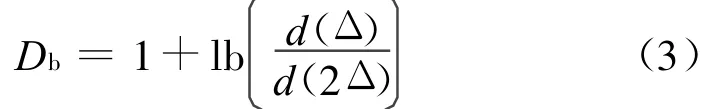
由式(3)可知,采样点与盒维数的稳定性之间的关系是单调关系。当信噪比SNR大于适当的值时,盒维数是稳定的。在一定SNR范围内,分形盒维数对噪声不敏感[6],由于噪声与信号的盒维数不同,文献[7]首先将分形盒维数引入到频谱感知中,提出可以利用盒维数的差异构建统计量进行频谱感知。本文选用高斯白噪声作为信号的噪声源,举例说明常见各类型调制信号与噪声分形盒维数如图1所示。

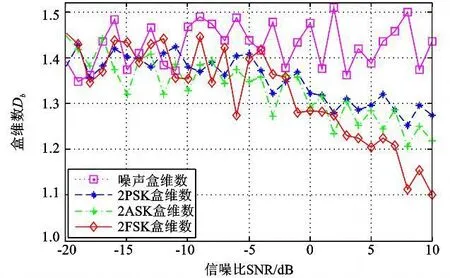
图1 调制信号与噪声盒维数Fig.1 Box dimension of modulated signals and noise

1.2 信息维数

首先对信号序列进行预处理,将信号序列变换到频域。由于信号频谱的形状主要取决于信号脉内的调制方式,在频域中进行特征提取可消除载频变化的影响。预处理后的信号序列为{fs(i),i=1,2,…,T},其中 T为预处理后信号序列的长度。频域进行重构以减少部分带内噪声的影响[8]:

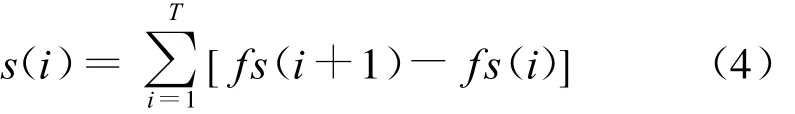
用D I表示分形信息维数,令

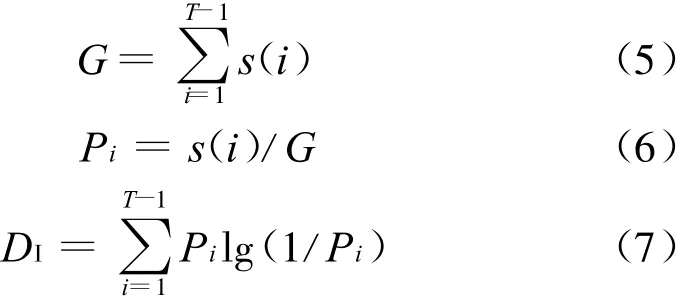
在-10～20 dB范围,每隔5 dB对信息维数作蒙特卡罗仿真 200次,可以得到常见的调制信号(2PSK 、QPSK 、MPSK 、LFM(线性调频)、2FSK、2ASK)信息维数均值与方差如表1所示。

表1 常见调制信号分形信息维数的均值、方差Tab.1 Mean value and variance of information dimension

2 分形维数协作感知

CUWB系统判断授权用户是否存在的过程,用H0表示不存在授权用户,认知用户可以切入该频段进行信号传输;反之,H 1表示授权用户存在,该频段正在被授权用户使用,认知用户不能切入或者必须立即退出该频段,避免给授权用户造成干扰。

2.1 协作检测理论

从图1可知,当信噪比较大时,接收信号的盒维数接近于本身信号的盒维数,受到噪声影响可以忽略。当信噪比较低时,接收信号的盒维数趋近于噪声的盒维数。噪声盒维数作为判决门限,由于门限在某一区间内波动,文献[7]仅仅取其中的一个值作为判决门限不够严谨合理,特别是在信噪比极低的情况下,易造成误判,导致判决出错。特别是在信噪比低于-15 dB时,将不能达到区别信号与噪声的目的。因此,借鉴文献[9]的双门限思想,将噪声分形盒维数区间作为判决不确定区 Ω,设定两个判决门限分别对应噪声分形盒维数的最大值和最小值。

因此,双门限盒维数检测判决准则可以重新定义为:

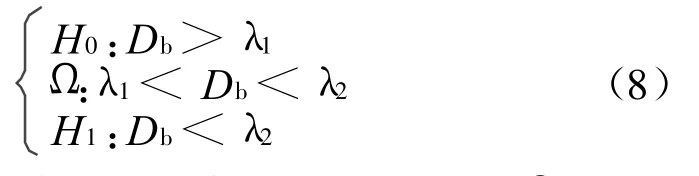
式中,Db表示接收信号的盒维数,当Db在 Ω中时,进行软判决,本地检测将检测统计量发送给CR控制中心;反之则采用硬判决,发送本地检测结果D b。

假设CR控制中心接收到Z个本地判决信息中,其中包括硬判决信息K个,记为β,软判决信息Z-K 个,记为α,软判决信息α可靠性融合准则为:

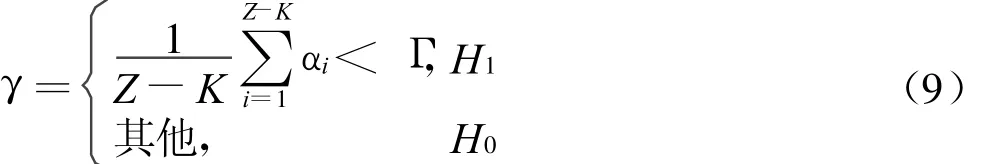
式中,Γ为可靠性融合的判决门限。Γ实际应用中可依据式(10)进行计算[10]。

最后,采用OR准则以最大化全局检测概率。CR控制中心利用β和γ进行最终判决:

然而,尽管双门限盒维数在检测判决门限上更为合理,有益于控制中心做出准确判决,但是,该方法不能够满足CUWB频谱感知对于信号调制样式识别的要求。盒维数只表示了信号的几何尺度情况,而没有反映信号在平面空间上的分布疏密,信息维数恰能做到这一点。信息维数对信号频谱形状进行复杂性量化,能够有效地容纳信号特征变化信息,对信号调制样式进行有效识别。因此,本文将信息维数引入频谱感知过程,进一步提高CUWB频谱感知的综合检测性能。

2.2 感知模型描述

为了满足超宽带系统频谱感知对检测率和信号调制样式识别的需求,本文提出将双门限盒维数与信息维数进行协作频谱感知,其感知模型可以构建为如图2的形式。

图2 分形维数协作频谱感知模型Fig.2 Fractal dimensions cooperative sensing model

2.3 理论分析

假设检测统计量Db在H0和H1情况下的分布分别为f(Db|H0)和f(Db|H1),则对应的累积分布函数(CDF)为:

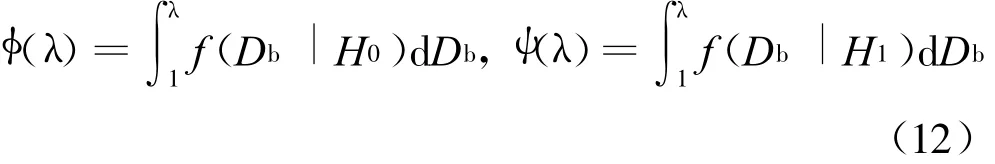
定义检测概率 P d、虚警概率 P f、漏检概率 P m、认知概率P c为:

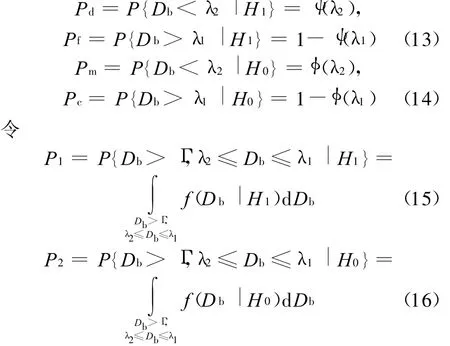
全局检测概率P d和全局虚警概率P f表示为:

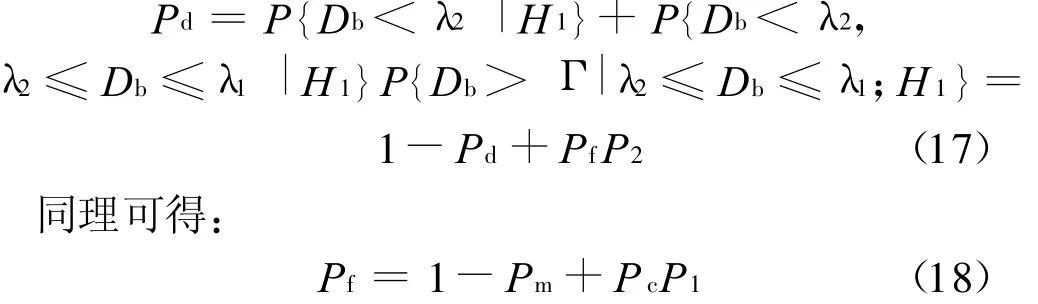
在运算复杂度上,双门限盒维数检测由于门限设定等运算,必然会带来一定的开销增加,但是有限的复杂度增加换来频谱检测率的提高是可行的;信息维数检测需要2T次加法运算和T次乘法运算,相对于循环谱特征检测运算复杂度为O=T2+(T/2)lb(T),信息维数有明显优势,从而缩短频谱感知时间。

3 仿真实现及分析

假设在加性高斯白噪声(AWGN)环境下,待检测的授权信号无信道衰落影响,设授权信号采用2PSK调制方式,信号采样点T=2 000,虚警概率Pf为0.01。作为对比,对能量检测性能进行了仿真,判决门限可参照文献[11]进行设定。由于噪声不确定的影响,可将噪声方差σ2的估计值表示为:σ-2=ξσ2,噪声不确定性以 d B的形式表示为:b=max{10lgξ},其中,ξ∈ [10-b/10,10b/10] 。

1)能量检测门限λed=1.05σ2,当噪声不确定性为1 dB,信噪比范围为-15～5 dB时,蒙特卡罗仿真500次。由图3可知,双门限合作频谱检测率高于单一门限盒维数检测和能量检测,尤其提高了在极低信噪比情况下的检测率。

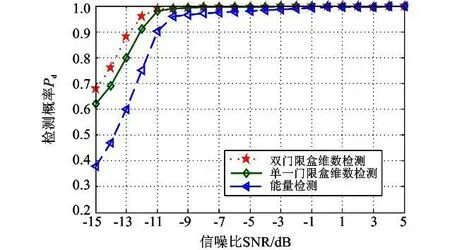
图3 不同方法检测效果对比Fig.3 Detection performance comparisonl

2)固定SNR为-12 dB,图4给出了3种方法对应的接收机工作特性(Receiver Operating Characteristic,ROC)曲线。由 ROC曲线可以看出随着虚警概率的增大,三种方法相应的检测概率得到提高,本文方法性能优于单一门限盒维数检测和能量检测。

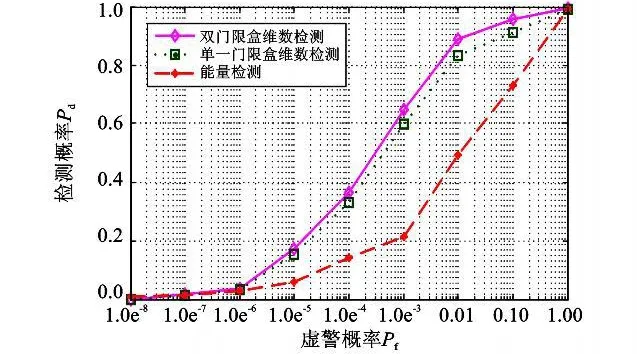
图4 3种方法ROC变化图Fig.4 ROC of three detection methods

3)采用信息维数对信号调制样式进行识别,当调制信号为2PSK时,在-10～16 d B范围,每隔2 dB对信息维数蒙特卡罗仿真200次,将信息维数对信号调制样式的识别效果与传统循环谱特征检测方法进行对比,如图5所示。

综上:1)双门限盒维数检测方法相对于单一门限盒维数检测和传统能量检测,检测性能更好,尤其提高了低信噪比频谱环境下的检测效果,其主要原因在于双门限方法,在选取盒维数检测门限上更为精确合理。2)信息维数检测相对于循环谱特征检测,能够取得更好的调制样式识别效果,特别是在低信噪比情况下更加明显,且信息维数检测复杂度低,所需检测时间短。3)结合双门限盒维数与信息维数的协作频谱感知方法,能够提高频谱检测率和识别信号调制样式,仿真效果明显优越,适合CUWB系统。

图5 调制样式识别效果对比Fig.5 Recognition performance comparison of modulation mode

4 结论

本文提出一种基于双门限盒维数和信息维数的CUWB协作频谱感知方法。首先,针对单一门限盒维数检测的不足,提出采用双门限盒维数方法,快速对授权信号进行检测,该方法对噪声不敏感,检测率高,运算复杂度低;然后,为了弥补双门限盒维数检测的不足,通过信息维数实现对信号调制样式的有效识别。仿真表明:该方法与循环谱特征检测相比,突出优点是计算复杂度低,频谱感知时间短。两者进行协作检测不仅能够提高检测率,更有利于区分有用信号、干扰信号及噪声,有利于控制中心做出正确判决并采取相应措施,达到提高频谱利用率的目的,尤其适合于在CUWB情景使用。

[1]Mitola J.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.

[2]Sonnenschein A,Fishman P M.Radiometric detection of spread spectrum signals in noise of uncertainty power[J].IEEE Transactions on aerospace electronic systems,1992,28(3):654-660.

[3]Cabric D,Brodersen R W.Physical layer design issues unique to cognitive radio systems[C]//Proceedings of IEEE International Symposium on Personal,Indoor and Mobile Radio Communications,2005:759-763.

[4]Digham F F,Alouini M S,Simon M K.On the energy detection of unknown signals over fading channels[J].IEEE Transactions on Communications,2007,55(1):21-24.

[5]许晓丹,毕光国,张在琛.循环功率谱特征检测算法在认知超宽带无线通信的应用[J].电子与信息学报,2008,30(10):2 435-2 438.XU Xiaodan,BI Guangguo,ZHANG Zaichen.Application of cyclic spectrum feature detection to cognitive UWB wireless communication[J].Journal of electronics&Information Technology,2008,30(10):2 435-2 438.

[6]吕铁军,郭双冰,肖先赐.调制信号的分形特征研究[J].中国科学E辑,2001,31(6):508-513.LV Tiejun,GUO Shuangbing,XIAO Xianchi.Fractal box feature research of modulated signal[J].Science in china(Series E),2001,31(6):508-513.

[7]赵春晖,马爽,杨伟超.基于分形盒维数的频谱感知技术研究[J].电子与信息学报,2011,33(2):475-478.ZHAO Chunhui,MA Shuang,YANG Weichao.Spectrum sensing in cognitive radios based on fractal box dimension[J].Journal of electronics&Information Technology,2011,33(2):475-478.

[8]张葛祥,胡来招,金炜东.雷达辐射源信号脉内特征分析[J].红外与毫米波学报,2004,23(6):477-480.ZHANG Gexiang,HU Laizhao,JIN Weidong.Intra-pulse feature analysis of radar emitter signals[J].Journal of infrared and millimeter waves,2004,23(6):477-480.

[9]Zheng X,Wang J,Wu Q,et al.A novel cooperative spectrum sensing algorithm in cognitive radio systems[J].Journal of communications and networks,2009,11(2):115-121.

[10]焦传海,王可人,冯辉.认知无线电中基于自相关矩阵的协作盲感知[J].电路与系统学报,2011,16(1):12-19.JIAO Chuanhai,WANG Keren,FENG Hui.Cooperative blind spectrum sensing based on autocorrelation matrix for cognitive radio[J].Journal of circuits and systems,2011,16(1):12-19.

[11]Ye Z,Memik G,Grosspietsch J.Energy detection using estimated noisevariancefor spectrum sensing in cognitive radio networks[C]//IEEE Wireless Communications and Networking Conference,Las Vegas,USA,2008:711-716.