基于贝叶斯原理的小子样试验导航误差评定方法

邓新文

(中国人民解放军91388部队,广东湛江 524022)

0 引言

近年来,水下无人航行器因其出色的隐蔽性、自主性和无人作战等特点,在各国的军事领域应用越来越多。无人航行器技术的飞速发展对航行器性能考核工作提出了更高的要求。长期以来,经典的试验分析与评估方法主要是以大子样试验为前提,但是,大子样试验是以昂贵的研制和试验费用以及试验周期长为代价的。如何通过小子样的试验来评估航行器导航误差(CEP)就成为了实践中急于研究解决的课题。小子样误差评定问题究其实质就是:在验前样本信息的基础上,如何利用标准试验现场少量的样本信息进行统计,评估无人航行器的导航误差。而贝叶斯定理是利用验前样本信息,通过有限样本来获取关注信息的普遍方法。1984年9月美军就采用贝叶斯小子样理论对“潘兴Ⅱ”导航的精度进行了评估[1],而以后的“天空闪光”导弹由于具有很强的技术继承性,作战鉴定次数只有6发,极大地节约了试验成本和时间,成为贝叶斯理论应用的经典范例。无人航行器通常采用自主导航加GPS组合导航方式,自主导航系统由惯导单元和多普勒计程仪构成,GPS用于校准自主导航误差。无人航行器的导航计算模块根据惯导单元测量的姿态数据和多普勒计程仪测量的绝对速度实时推算航行器经纬度坐标。自主控制模块依据当前位置与目标位置的相对关系,自行调整航向、航速、深度等航行参数引导航行器到达目标位置。航行器当前的推算位置与目标位置偏差不大于某一范围即位置控制范围时,航行器认为到达该点。虽然对于在无线电波不能到达的水下位置,无法用无线电手段直接测量航行器在目标点的定位误差,但只要获得了推算位置与GPS等校准设备获取的实际位置之间的偏差即导航误差就可以评估航行器到达目标点的定位误差。据了解,目前国内外还没有一种行之有效的方法来考核和验证航行器导航误差。这里提出一种利用贝叶斯原理通过有限小子样来评定导航误差的方法。

1 背景

1.1 CEP概念

一般用CEP来衡量导航误差。CEP简单来说等于无人航行器以概率0.5进入以目标点为圆心的圆域的半径r。CEP可用概率公式表示为:

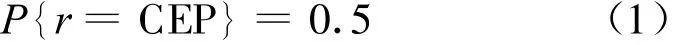
1.2 验前信息

无人航行器参加正式评定试验前,在研制过程中需进行大量的导航精度试验,这些验前信息对于运用贝叶斯理论是十分宝贵的。贝叶斯理论要求验前信息与验后信息近似服从同一总体,因此获取验前信息后,接着需要进行验前子样与验后子样的相容性检验。关于相容性检验方法可参考文献[2]。可信度用于度量验前子样与验后子样属于同一总体的可信程度。这里认为,当相容性检验通过时,验前子样的可信度近似为1。

1.3 验前子样的去相关性处理

根据以往大量试验可知,无人航行器的纵、横向偏差(ΔH,ΔL)一般服从正态分布。考虑到无人航行器纵、横向偏差的相关性,对验前子样散布中心数据首先要进行正交变换,以消除纵、横向偏差间的相关性。纵、横向偏差 ΔH,ΔL的相关系数γ可以参照弹道仿真的方法来获取。

验前子样一般具有独立性,即各次试验相互独立。考虑到验前子样μΔH散布中心数据存在系统偏差μΔH和 μΔL,则验前子样的纵、横向偏差(ΔH,ΔL)～ (μΔH,μΔL,σΔH,σΔL,γ)。应用文献[3] 给出的正交变换方法,将(ΔH,ΔL)的 CEP评定问题转换为(ΔH′,ΔL′)的 CEP 评定问题 。

2 贝叶斯评定

无人航行器导航偏差的样本空间可以划分为两个子空间,即可形成两个假设,设CEP指标为R则有:

1)根据验前数据(ΔH′,ΔL′),航行器进入以目标为圆心、半径为R的圆域,表示为H 0:r=R;

将处理后的验前子样数据(σΔH′,σΔL′)代入CEP计算公式[4-5]求出H0的概率P(H0),而H 1的概率

设 ρ= ΔH′2+ΔL′2表示正交转换后纵、横向偏差矢量的模,则 ρ1,…,ρn是相互独立的,根据(ΔH′,ΔL′)的统计分布特征计算ρ的概率密度函数为f(ρ)。当正交转换后纵向偏差的均方差与横向偏差的均方差相等,记为 σ,则 ρi(i=1,…,n)服从瑞利分布,即:

在H 0条件下,航行器进入以目标为圆心、半径为R的圆域的概率为P(H0);在H1条件下,航行器进入以目标为圆心、半径为R的圆域的概率为P(H1)。由CEP计算公式,当纵、横向偏差相等时,可得H 0条件下的方差记为σ0,H 1条件下的方差为σ1。

对于验前样本空间中的任何一个子样ρi(i=1,…,n),在H 0条件下其值小于等于R的概率为:

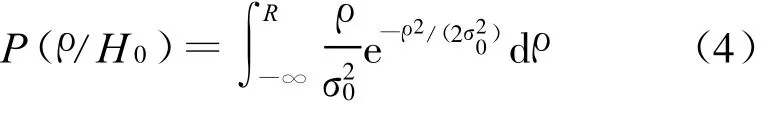
在H 1条件下其值小于等于R的概率

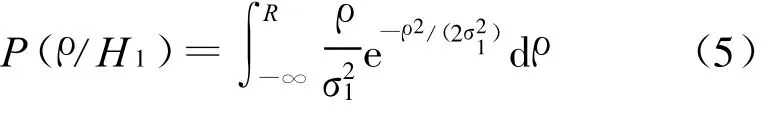
由贝叶斯定理,得验后子样ρ≤R条件下H 0成立的概率为:

采用式(6)可以根据一个样本的试验结果推断成立的概率,但还不能确定H 0是否成立。本文采用多个样本的贝叶斯推断方法来评定导航误差,样本数不大于3个,具体步骤为:

1)根据第一个样本结果,推断H0成立的概率是否小于等于0.5,如果大于0.5则认为成立,否则转至步骤2);

2)根据第一、二个样本的试验结果,推断 H0成立的概率,如果大于0.5则认为成立,否则转至步骤3);

3)根据第一、二、三个样本的试验结果,推断H0成立的概率,如果大于0.5则认为成立,否则转至步骤4);

4)重新评定。

3 小样本CEP评定实例

设无人航行器CEP指标为1%D,D为航程。验前子样有20个,通过验前子样数据的统计计算得到导航误差满足1%D的概率为0.9,即P(H0)=0.9,则 P(H1)=1-P(H0)=0.1。根据式(4)和式(5)计算得 P(ρ/H0)=0.9,P(ρ/H1)=0.1。

求1)第一个验后子样航行器且距目标点的偏差ρ小于1%D,无人航行器导航精度是否满足指标要求?2)在条件1)下如果验后第一个子样导航精度不满足指标,求无人航行器导航精度不满足导航精度指标的概率有多大?3)若第一个验后子样导航精度不满足指标,还需要几个子样就可评定导航精度?解:1)当验后子样距目标点偏差小于1%D时,无人航行器导航误差小于或等于1%D的概率为:

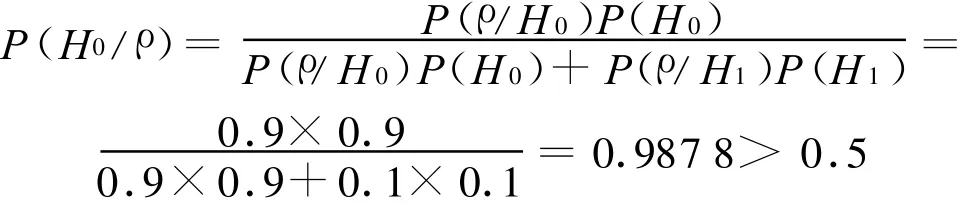
因此可判定无人航行器导航精度指标满足0.1%D的CEP。

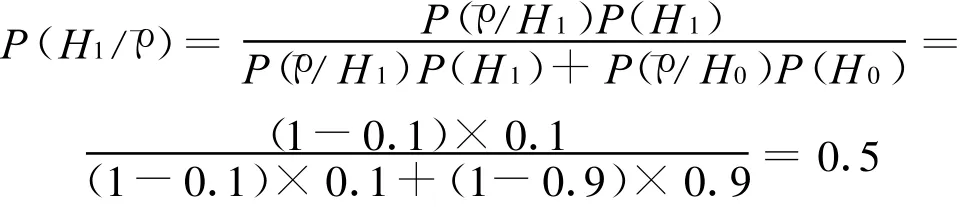
2)当验后子样距目标点偏差大于1%D时,无人航行器导航精度不满足1%D的概率为:说明根据第一子样的试验结果无法判定导航精度不满足指标要求,需要继续进行试验来评定导航指标。

3)第一个子样ρ1不满足指标,第二个子样ρ2的结果有两种可能:①不满足指标;②满足指标。

首先讨论情况①。此时无人航行器导航精度不满足指标的概率为:

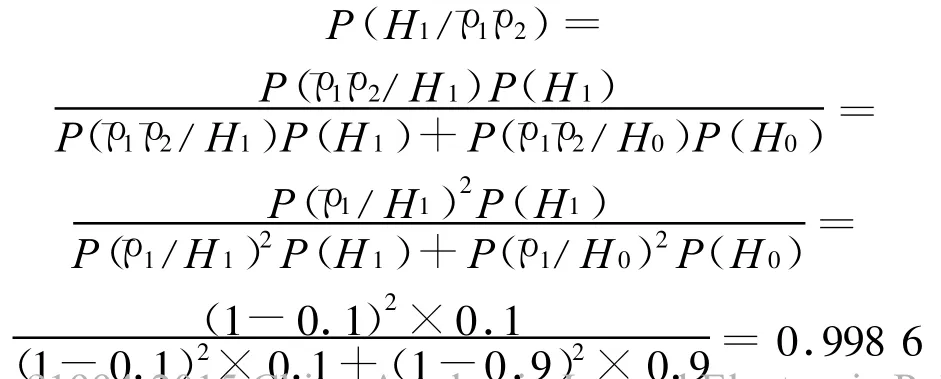
根据实际推断原理,如果前两次试验的导航精度达不到指标要求,则可判定无人航行器导航精度不满足指标。

对于情况②第一个子样不满足要求,第二个子样满足要求,则需要进行第三次试验,根据第三次试验的结果来评定导航精度是否满足指标要求。

如果第三次试验精度还不满足要求,则有

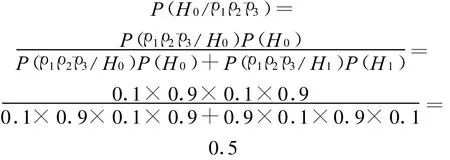
则仍无法判定导航精度是否满足要求,需重新组织进行正式的评定试验。

如果第三次试验精度满足要求,则有

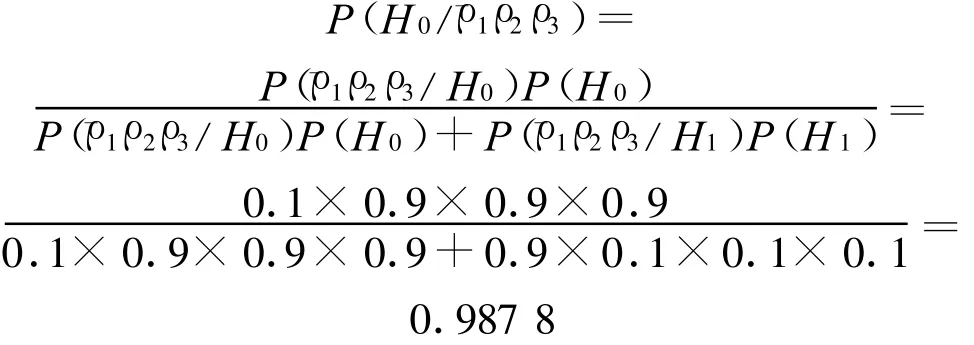
可判定导航精度满足指标要求。

实例中,贝叶斯评定过程和结果见表1,其中√表示满足,×表示不满足,/表示此次试验不进行,△表示需重新组织评定试验。

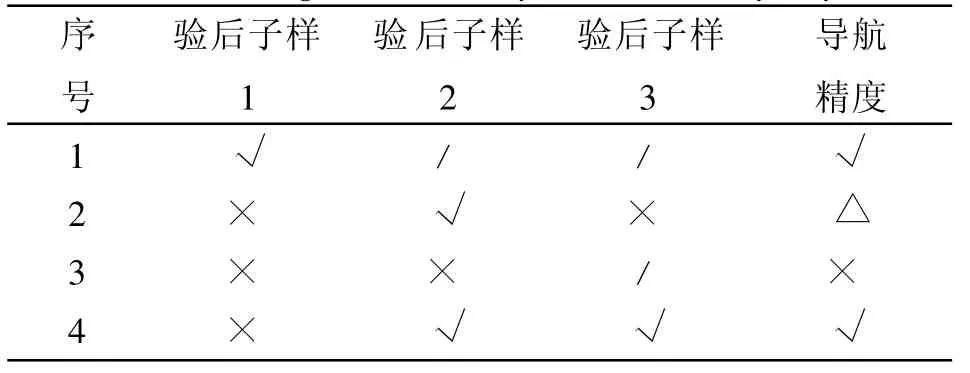
表1 运用贝叶斯理论评定导航精度Tab.1 Navigation accuracy assessment by bayes

如表1第1行,本实例只需要3个验后子样。如表1第2行所示,如果验后子样1的导航误差不大于1%D,则无需进行第二、三次试验,可直接判定精度满足1%D的CEP指标。否则,如果验后子样1的导航误差大于1%D,则需要进行第二、三次试验,接着根据验后子样2的试验结果对可能出现的以下两种情况分别进行判定。

情况1)如果验后子样2的导航误差不大于1%D,则需进行第三次试验,如果验后子样3的导航误差仍不大于1%D,则可判定导航精度满足1%D的CEP指标,如表1第5行所示;如果验后子样3的导航误差大于1%D,如表1第3行所示,则无法判定是否满足指标要求,需重新组织评定试验;

情况2)如果验后子样2的导航误差大于1%D,则可判定导航精度不满足1%D的CEP指标要求,如果表1第4行所示。

从实例可知,本方法至多经过三次试验可以判定导航精度是否满足指标要求,能够显著减小试验时间和成本,提高评定效率。

4 结论

本文提出一种无人水下航行器导航误差的小子样试验评定方法。该方法综合运用大量验前子样,对其进行相容性检验,以确定有效的验前子样,并运用统计推断理论获取验前信息。根据在验收试验中获取的验后子样获取验后信息,利用贝叶斯理论推断无人航行器满足CEP指标的概率,完成导航误差评定。实例表明:该方法在海上试验中得到了成功应用,可以大幅度减少试验成本,缩短试验时间,提高评定效率,为无人水下航行器导航误差的评定提供了一种简便而且有效的方法。

[1]WbodroofeM W,WillardD,SingPurwallaN D,et al.PershingⅡfollow-ontest:size reduced by sequential analysis AD-A 192136[R].US:Washington,2005.

[2]吴东坡,肖金友.小子样条件下弹头落点CEP计算方法[J].现代防御技术,2002,30(3):28-32.WU Dongpo,XIAO Jinyou.A method of evaluating CEP of warhead impact point on condition of small sub-sample[J].Modern Defence Technology,2002,30(3):28-32

[3]张湘平.小子样统计推断与融合理论在武器系统评估中的应用研究[D].北京:国防科技大学,2003:83-86.

[4]金忠.圆概率偏差的测定与检验[J].南京理工大学学报,1995,19(2):135-138.JIN Zhong.Estimation and test of circular error probability[J].Journal of Nanjing University of Scienceand Technology,1995,19(2):135-138.

[5]David A Shnidman.Efficient Computation of the Circular Error Probability(CEP)Integral[J].IEEE,Transactions on Automatic Control,1995,40(8):1 472-1 474.