基于磁强计/陀螺的卡尔曼滤波定姿算法

张晓霞,曹咏弘

(中北大学理学院,山西太原 030051)

0 引言

在组合导航系统中,姿态解算是一个重要的研究课题。陀螺是最常用的姿态传感器,但是高性能陀螺的体积大、价格高,限制了陀螺在某些领域的应用。近年来,MEMS陀螺由于其体积小、成本低、易于批量生产,因而在各大领域受到青睐。

对陀螺测得的三轴姿态角速率积分可以确定姿态,但其测量精度易受陀螺角速率误差的影响,会在短时间内引起较大的误差,解决该问题常用的方法是采用卡尔曼滤波器[1-3]。卡尔曼滤波器利用来自加速度计、磁强计、倾斜计等传感器的数据来补偿陀螺引起的误差。随着低成本固态惯性器件和磁传感器件的发展,利用MEMS陀螺和磁强计进行姿态探测是近年来测量系统研究的热点之一。文献[1]设计了一个利用加速度计和磁强计来补偿误差的扩展卡尔曼滤波器。结合对重力场和地磁场的测量,使用高斯-牛顿迭代法求解非线性方程组,从而获得四元数。该算法不仅使用了对重力场的测量,而且要求载体处于静止或不存在线加速度。因此,该算法具有局限性。文献[2]采用磁强计和陀螺来测量姿态角。该算法是先通过磁阻传感器来确定滚转角,再利用公式计算另外两个姿态角,从而获得姿态四元数。但在磁阻传感器测姿态角一节中,计算滚转角的公式只描述了一种特殊情形,因而具有片面性。文献[3]提出了一种采用磁强计和MEMS陀螺构建低成本姿态探测系统的方案。该算法利用“先验弹道信息”辅助磁强计的测量,获得滚转姿态角,随后利用递推算法获取另外两个姿态角,从而获得姿态四元数。该算法必须事先获得弹道的先验信息,再结合磁强计的数据对陀螺误差进行补偿,因而限制了该算法的运用。

本文针对以上算法的不足和限制,提出了一种磁强计和MEMS陀螺组合确定姿态的四元数卡尔曼滤波方法。

1 方向余弦四元数

确定弹丸的姿态就是确定载体坐标系(b)相对于惯性坐标系(n)的位置,为避免出现奇异,弹丸的姿态通常由四元数形式的方向余弦矩阵确定。式

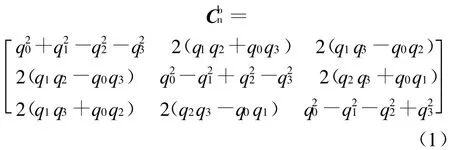
(1)中,四元数 q0、q1、q2、q3约束方程为(t)+(t)+q22(t)+q23(t)=1,方向余弦矩阵在姿态确定中起着重要作用,由此方向余弦矩阵还可以求出姿态角。

2 磁强计与陀螺组合的卡尔曼滤波定姿算法

2.1 卡尔曼滤波定姿算法的状态方程

公式(2)为描述四元数变化规律的四元数微分方程[4]:

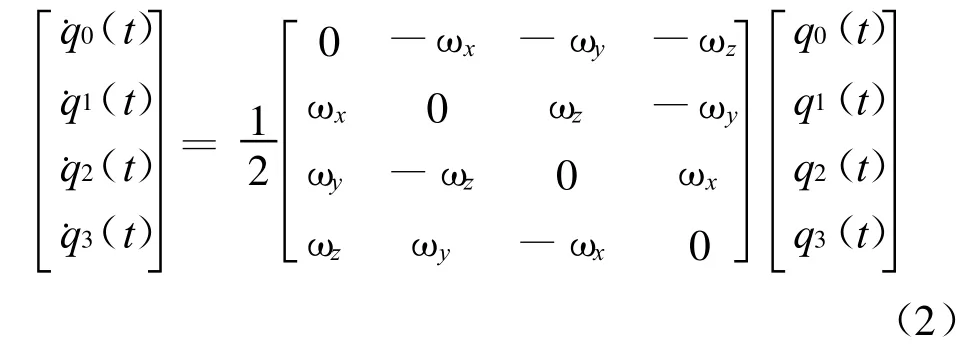
式(2)中,ωx,ωy,ωz为安装在弹轴上的陀螺测量的角速度分量。

把式(2)当做状态方程,并取q(t)=[q0(t)q1(t)q2(t)q3(t)]T为状态向量,由于该方程是连续的,应用比卡逼近法[5]将其离散化,得到:

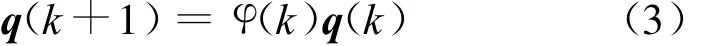
公式(3)就是离散化的状态方程。其中:

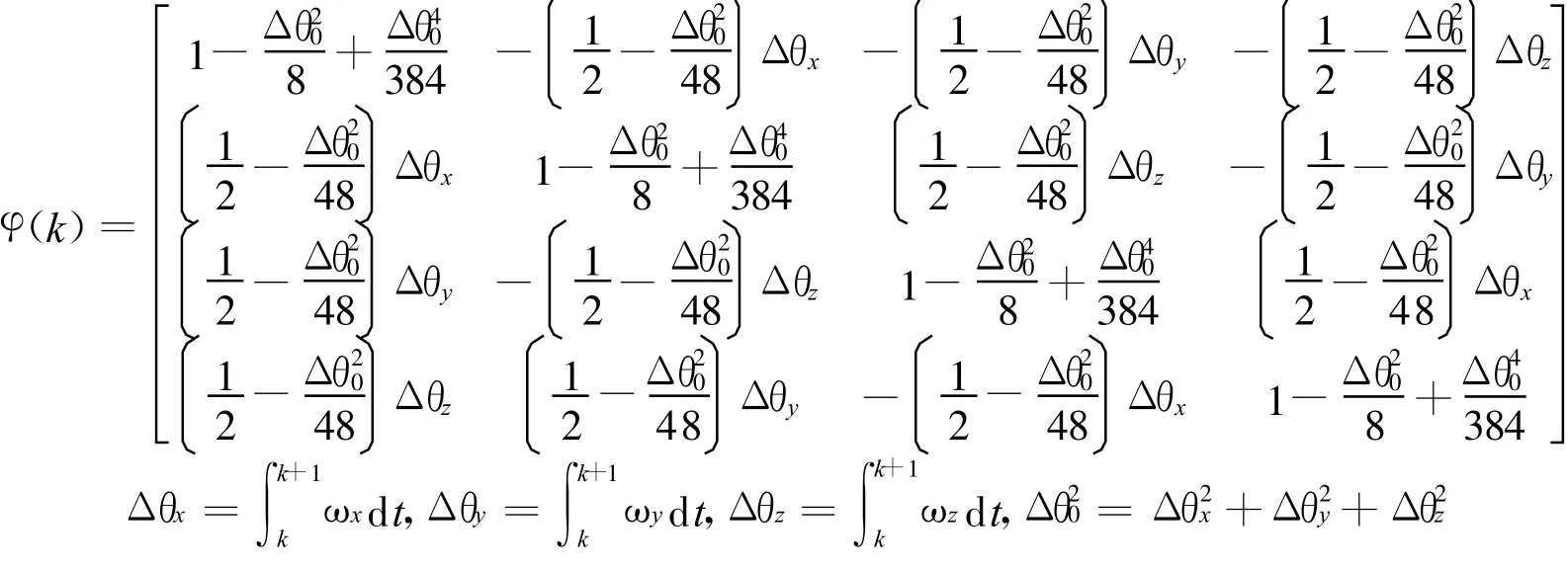
2.2 卡尔曼滤波定姿算法的观测方程

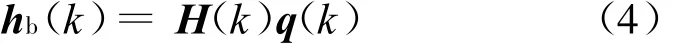
公式(4)即为观测方程,该方程的特点是H(k)矩阵中含有状态变量q(k)。其中:

2.3 卡尔曼滤波定姿算法

由于实际问题都是含有噪声的,所以反映实际问题的状态方程和观测方程如下:

式中,W为均值为零方差为Q的系统白噪声,V为均值为零方差为R的量测白噪声,且W与V不相关。T为4阶单位阵。

下面给出卡尔曼滤波器递推算法[6]:预测、估计误差方差阵分别为:

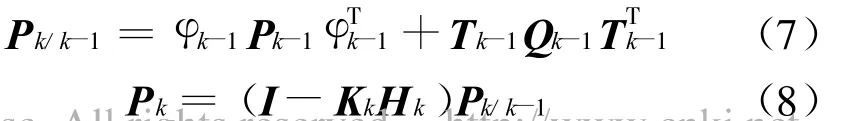
增益矩阵为:

预测、估计状态分别为:

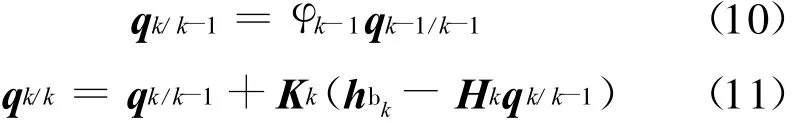
卡尔曼滤波是一种递推算法,该算法充分利用陀螺输出的角速率信号和磁强计输出的地磁信号,适当权衡两方面的信息,得到对状态q(k)的最优估计,且状态每一次更新估计都是由前一次估计和新的输入数据计算得到,因此,只需储存前一次的估计,即可实现实时处理。

3 仿真实验

以工程实际问题为仿真背景,对由陀螺和磁强计构成的组合测试系统进行数值仿真。仿真参数如下:仿真时间为20 s,算法采样周期为0.01 s。取太原为实验地,该地区磁倾角I=55°,磁偏角α=4°,垂直分量为:0.43×10-4T,水平分量为:0.31×10-4T。

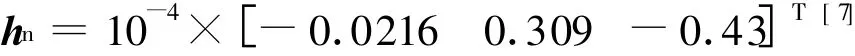
仿真中:假定陀螺为均值为零,方差为0.1(°)/s的白噪声,磁强计为均值为零方差为0.000 1T的白噪声,卡尔曼滤波器初值分别为:

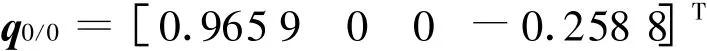
其对应的均方误差阵为:

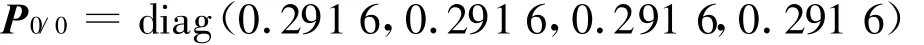
仿真实验结果如图1—图3所示。

从仿真实验结果可知:运用卡尔曼滤波算法进行最优估计姿态角误差不随时间积累,被控制在一定范围之内。偏航角误差保持在±0.5°之内,俯仰角误差也在±0.48°,而滚转角误差也被控制在±0.5°。因此,上述模型解算姿态角算法简单,易于操作,从一定程度上抑制了误差的积累,解算精度有了明显提高。

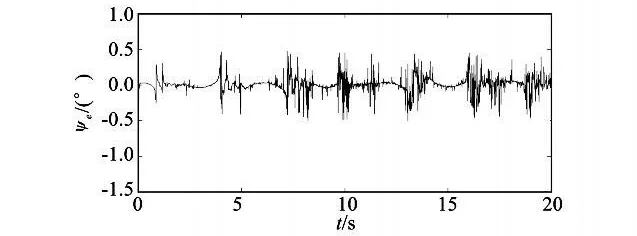
图1 偏航角误差曲线图Fig.1 Error curve of yaw angle

图2 俯仰角误差曲线图Fig.2 Error curve of pitch attitude

图3 滚转角误差曲线图Fig.3 Error curve of roll angle

4 结论

本文提出了一种基于磁强计与陀螺组合确定姿态的卡尔曼滤波算法。该算法利用陀螺测量的姿态角速率,结合磁强计输出的地磁分量,运用卡尔曼滤波算法对三个姿态角同时进行最优估计,而不需要先验假设。仿真结果表明:估计误差较小且不随时间积累,即算法可行。应该指出的是:影响陀螺磁强计组合姿态测量精度的因素有很多,在这里仅考虑了白噪声对系统的影响,其他因素的影响有待于进一步的研究。

[1]黄旭,王常虹,伊国兴,等.利用磁强计及微机械加速度计和陀螺的姿态估计扩展卡尔曼滤波器[J].中国惯性技术学报,2005,13(2):27-30.HUAN Xu,WANG Changhong,YI Guoxing,et al.Extended Kalman Filter for IMU attitude estimation using magnetometer,MEMS accelerometer and gyroscope[J].Journal of Chinese Inertial Technology,2005,13(2):27-30.

[2]崔敏,马铁华,段精婧,等.基于磁强计和陀螺的弹箭飞行姿态测试方法[J].弹箭与制导学报,2010,30(6):85-87.CUI Min,MA Tiehua,DUAN Jingjing,et al.Missile/rocket flight attitude test method based on magnetometer and gyroscope[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(6):85-87.

[3]鲍亚琪,陈国光,吴坤,等.基于磁强计和 MEMS陀螺的弹箭全姿态探测[J].兵工学报,2008,29(10):1 227-1 231.BAO Yaqi,CHEN Guoguang,WU Kun,et al.Research on attitude determination using magnetometers and MEMS inertial sensors[J].Acta Armamentarii,2008,29(10):1 227-1 231.

[4]刘建业,曾庆化,赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010.

[5]邓正隆.惯性技术[M].哈尔滨:哈尔滨工业大学出版社,2006.

[6]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社,2004.

[7]曹咏弘,祖静,林祖森,等.基于加速度计与磁强计组合的子弹姿态虚拟测试[J].测试技术学报,2004,18(S5):42-45.CAO Yonghong,ZU Jing,LIN Zusen,et al.Virtual test of attitude of bullet based on the accelerometer and magnetometers combination[J].Journal of Test and Measurement Technology,2004,18(S5):42-45.