水下结构物低频振动相关性及声辐射特性分析

关珊珊，曹为午，陈 明

(武汉第二船舶设计研究所，湖北 武汉 430064)

0 引言

水下结构物推进器激起的结构声辐射对总体噪声水平有重要影响。推进器的激振力通过尾部轴承和推力轴承传递给结构引起水下辐射噪声，随着频率的提高，推进器产生的激振力急剧下降［1］，水下结构物的较高振型难以激励出来，因此推进器激振力引起的噪声主要是低频噪声。在低频段其量级甚至可能超过推进器自身的噪声水平，是水下结构物的主要噪声源之一。

振动相关性普遍存在于水下结构物低频总振动中，对于由于推进器运行引起的水下结构物的低频振动，纵向和横向(垂向)振动的相关性研究具有重要意义。本文基于有限元边界元理论给出水下结构物低频动力学模型及求解方法［2］，讨论了舷间、舷外附连水以及大型机组基座、舱内铺板、设备等对航行器低频振动特性的影响。在此基础上，研究了推进器通过轴系纵向激励引起的低频弯曲振动与纵向振动的相关性，并进行声辐射计算分析。研究结果对理解推进器交变力作用下的水下航行器低频声辐射的形成过程有实质性的意义。

1 基本原理

流固耦合力学的一个最重要特征是流体与固体两相介质之间的相互作用，即可变形的固体在流体荷载的作用下会产生变形或运动，而变形或运动又反过来影响流场的状态，从而改变流体荷载的分布和大小［3－4］。正是这种两相介质之间的相互作用将在不同条件下产生形式各异的流固耦合现象。

1.1 水下弹性结构物振动有限元矩阵方程

真空中含有阻尼的弹性结构振动的有限元矩阵方程可表示为［5］:

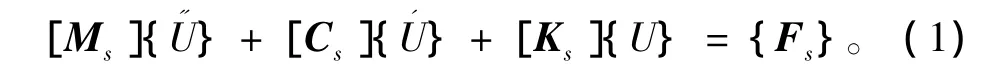
其中:［Ms］为结构质量矩阵;［Ks］为结构刚度矩阵;［Cs］为结构阻尼矩阵;{Fs}为结构载荷力向量。

当 {Fs}=0，并取［Cs］=0，则有

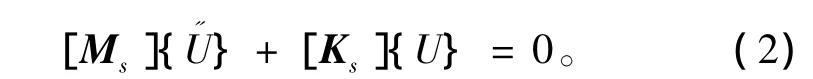
利用本征向量的正交性，可以给出真空中结构的本征模态和对应的本征值、模态频率。

当弹性结构置于声学介质中时，在流体与结构的交接面S上流体与结构之间存在着相互作用，声压对结构产生一个面力的作用。根据虚功原理可将该面力等效移置到单元节点上，于是，弹性结构与声场的耦合振动矩阵方程为:

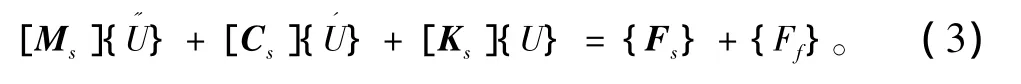
式中:{Ff}=［R］T{P}。

将式(1)和式(3)联立，可写成统一的矩阵方程:

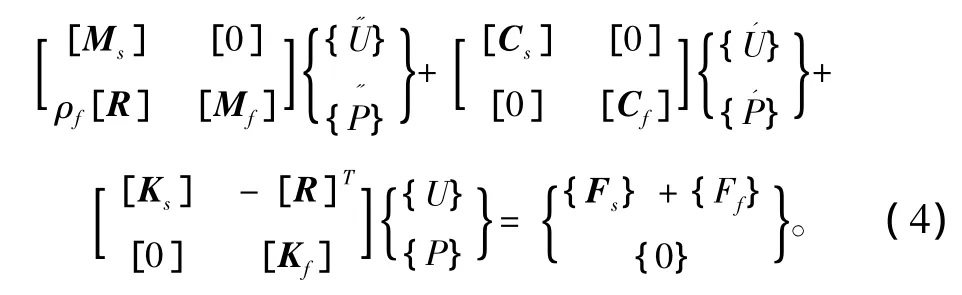
根据式(4)可以得到结构表面S节点处的位移和声压。当将边界∑上的声边界阻尼取为全吸收时(即满足远场条件时，在该边界上的声阻抗为平面波阻抗)，可近似计算在无界流体区域内弹性结构与流体的耦合振动和声辐射问题。

对于求解系统固有频率时，可以将系统视为无阻尼的自由系统。式(5)可写成:

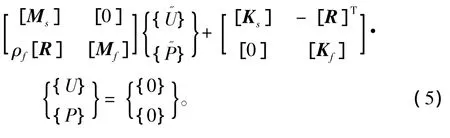
1.2 耦合振动特性的求解

传统的FEM/BEM法求解水下结构物振动声辐射，是利用有限元法(FEM)求解出结构在流固耦合情况下的响应，即结构在受到外部激励情况下的表面位移或速度，然后再利用边界元法(BEM)求解出结构周围的流场在此响应下的声压［6］。由于整船模型非常复杂，采用有限元进行离散后，离散过程中所形成的刚度阵［K］及质量阵［M］相当庞大，求解动力方程时的计算工作量比较大。整船在真空中的振动特性，由于所形成的［Ks］和［Ms］矩阵为对称阵，动力方程式(2)的求解较易。但与附连水耦合后，动力方程变为式(5)，动力方程中的耦合刚度阵和质量阵为非对称阵，矩阵一旦庞大，完全采用有限元求解流固耦合动力响应方程具有很大困难，且极易出现奇异解。对于流固耦合下结构的特征频率和振型，完全采用FEM获取也存在相同的问题。

本文现利用结构“干模态”求解结构在流场中的“湿模态”，避免了利用有限元求解大型流固耦合方程，即忽略流体刚度，此时流场中结构振动控制方程式(5)可写为式(6)，式中{Ug}为与流场耦合后的结构位移。由有限元求解方程式(2)获得结构刚度阵Ks、质量阵Ms以及振型{U}。采用由“干模态”下的整型{U}来解耦式(5)中的刚度阵Ks、质量阵Ms以及Mf。此时，真空中的结构刚度阵Ks、质量阵Ms相对于真空中的振型{U}解耦。

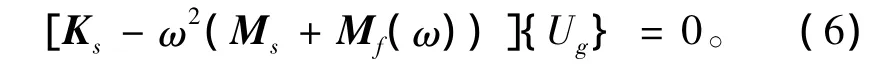
2 水下结构物低频振动特性

建立水下结构物有限元模型，包括:内壳、外壳、舷间结构、隔舱壁以及内部结构、设备、大型基座、舱内大型铺板以及电机等设备，如图1所示。讨论舷间、舷外水以及大型机基座、铺板、设备等对低频振动的影响，以“干模态”第一阶弯曲频率为基准归一化，计算结果见表1。

图1 数值模型Fig.1 Finite element model

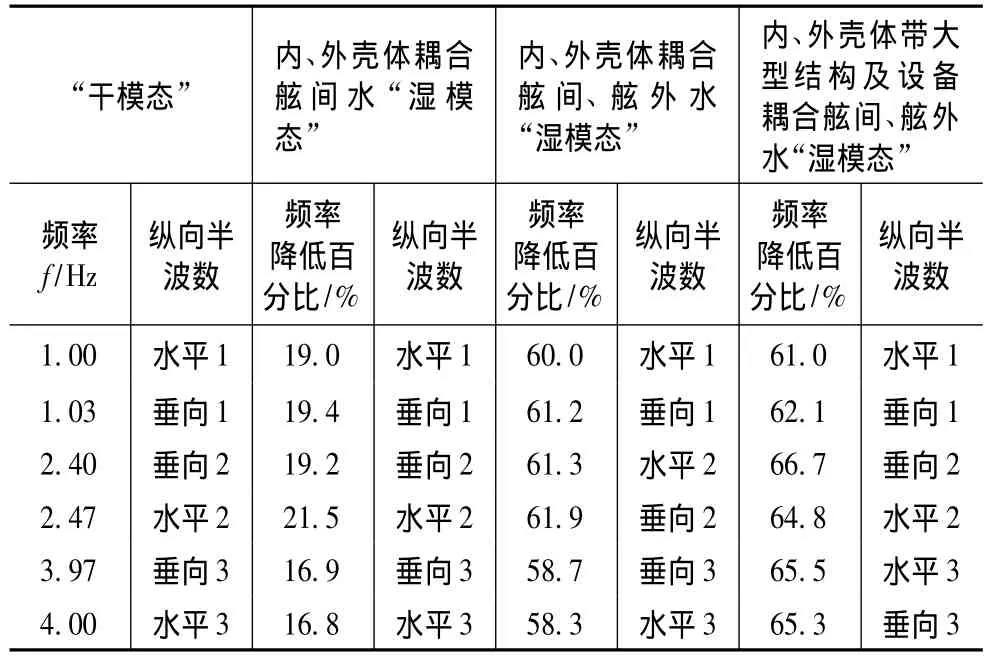
表1 低频振动固有频率对比Tab.1 Comparison of characteristic frequencies of low models

从表1对比可知，耦合舷间水后固有频率较“干模态”中的略低，在与舷外流体耦合后其固有频率变化较大，“湿模态”固有频率接近于“干模态”固有频率的一半;大型基座、铺板等结构及设备等对一阶弯曲(横向、垂向)模态频率影响不大，随着纵向半波数增加，影响逐渐增大。

3 推进器纵向交变力引起的各向振动声辐射相关性

结构物总体弯曲振动与纵向振动的相关性评估，对理解在推进器交变力作用下引起低频声辐射的振动形成过程有着实质性的意义。

结构物尾端在受推进器纵向单位交变力作用下时，进行结构表面测点的各向振动特性分析。振动计算结果见图2，声辐射特性计算结果见图3。从图中分析可知，振动相关性普遍存在于结构总振动中，由于弯曲振动具有比纵向振动小得多的波长，因此，它们对横剖面的刚度中心和质量中心沿纵向长度局部的偏离反应敏感。

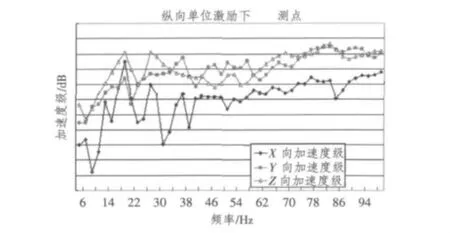
图2 推进器纵向激励下测点振动加速度谱线Fig.2 Vibration accelerations of the surface point of a vessel by prepeller vertical-excited

图3 推进器纵向激励下辐射声压级Fig.3 Raiation of a vessel by prepeller vertical-excited

4 结语

水下结构物推进器激起的结构声辐射对总体噪声水平有重要影响。在水下结构物声振特性计算分析中，应充分考虑舷间、舷外水的耦合作用，尤其是舷外水的耦合作用。

由于实际的水下结构物结构在满足总体稳性的预先前提下，其剖面的刚度中心和质量重心有一定的偏离。因此，在推进器的力作用下，从轴承传递给结构的干扰力的纵向分量与结构物中轴的不重合，以及结构物本身的刚度中心与质量中心的不重合，会导致结构物的弯曲振动。由于弯曲振动具有比纵向振动小得多的波长，它们对横剖面的刚度中心和质量中心沿纵向长度局部的偏离反应敏感，由于这种相关性在水下结构物振动特性中普遍存在。因此，在推进器力作用下，低频振动声辐射不仅仅取决于推进器作用于作用力(纵向、横向及垂向)的特性及量值，而且还决定于结构物不同振动形式间的相关性。

［1］陆鑫森，金咸定，刘涌康.船体振动学［M］.北京:国防工业出版社，1980.195 －198.

［2］彭旭，骆东平.船舶结构建模及水下振动和辐射噪声预报［J］.噪声与振动控制，2003，12(6):9 －11.PENG Xu，LUO Dong-ping.The modeling of the ship and numerical simulation of coupled vibro-acoustic behavior by FEM/BEM［J］.Noise and Vibration Control，2003，12(6):9 －11.

［3］FAHY F.Sound and structural vibration:radiation，transmission and response［M］.Academic Press，London，1985.

［4］DOWELL E H， GORMAN G F， SMITH D A.Acoustoelasticity:general theory，acoustic natural modes and forced response to sinusoidal excitation，including comparisons with experiment［J］.J.Sound Vib，1977，52(4):519－542.

［5］叶先磊，史亚杰.ANSYS工程分析软件应用实例［M］.北京:清华大学出版社，2003.18 －34.

［6］孙焕初，张立洲，许强，等.无奇异边界元法［M］.大连:大连理工大学出版社，1999.3－5.