大型发电机现场动平衡影响系数分析及应用

俞 辉，常 强，冷 杰

(1.辽宁省电力有限公司大连培训中心，辽宁 大连 116000;2.东北电力科学研究院有限公司，辽宁 沈阳 110006)

某国产空冷汽轮发电机组启动后发电机前轴承及滑环处小轴承振动偏大，现场动平衡后，振动大幅减小，但滑环处小轴承振动仍超标。2008年8月，电厂决定在停机间歇再次进行动平衡调整。

为了提高动平衡的准确性、确保平衡调整一次成功、减少电厂损失，需要对以往的平衡数据进行分析[1]。

1 影响系数法动平衡原理

机组轴系振动符合标准时，可看作一个线性动力系统，输入为各加重平面的加重量，输出为各振动测点的工频振动值。输入和输出值均为有幅值和相位的向量，在计算时用复数表示。在第i个平面零度角位置添加单位质量引起的第j个测点振动值称为i平面对j测点的影响系数。

用影响系数法进行动平衡分2步:首先在选定平面上添加试重，计算出影响系数;然后根据影响系数求解出平衡配重。

在试验中，由于影响机组振动的因素较多，并且允许添加试重的次数有限，很难获得准确的影响系数，从而导致平衡失败。因此对现有数据分析与甄别、合理出具选择与处理将决定平衡工作的成败[2－3]。

2 机组以往平衡概况

该机组轴系共4个转子，9个轴承[4]，图1为轴系示意图。

图1 轴系示意图

2007年机组首次启动后，7号瓦、9号瓦振动偏大，具体数据见表1。

表1 机组首次启动发电机振动数据

2007年11～12月，进行了4次现场动平衡调整，具体如下:

a. 11月10日，低发对轮加重766 g∠338°，机尾小盘去重270 g∠138°;

b. 11月12日，低发对轮去掉上次加重，添加配重400 g∠83°，机尾小盘加重90 g∠145°;

c. 12月1日，机尾小盘加重91 g∠165°;

d. 12月1日，机尾小盘去掉上次加重，再加重 90 g∠278°。

经过以上配重调整后，发电机振动明显好转，具体数据见表2。

表2 现场平衡后发电机振动数据

3 影响系数计算

机组以往平衡过程中，为了减少启动次数，假设在低发对轮上加重不会显著影响9号瓦振动，前2次平衡调整为同时在低发对轮和机尾小盘上加重。这种假定有时会带来大误差。因此，为了求得准确的影响系数，应选取在机尾小盘单独加重的数据计算。

后2次配重调整是单独在机尾小盘上加重。因此以第2次加重后的状态作为初始状态，可以求得3组影响系数。

计算影响系数时，首先要保证所选数据的准确性。一般要求数据选取段机组振动值比较平稳，不存在其它影响振动的因素，如动静碰磨、转子热弯曲等，由于现场动平衡任务的紧迫性，这种要求往往难以达到，以致数据中含有非动平衡因素成分。由此计算结果会有较大误差。此时可选取一段数据求复数平均值后再计算，能一定程度上提高计算精度[5]。

选取3次加重后振动数据中较为平稳的一段求平均值，计算结果见表3。

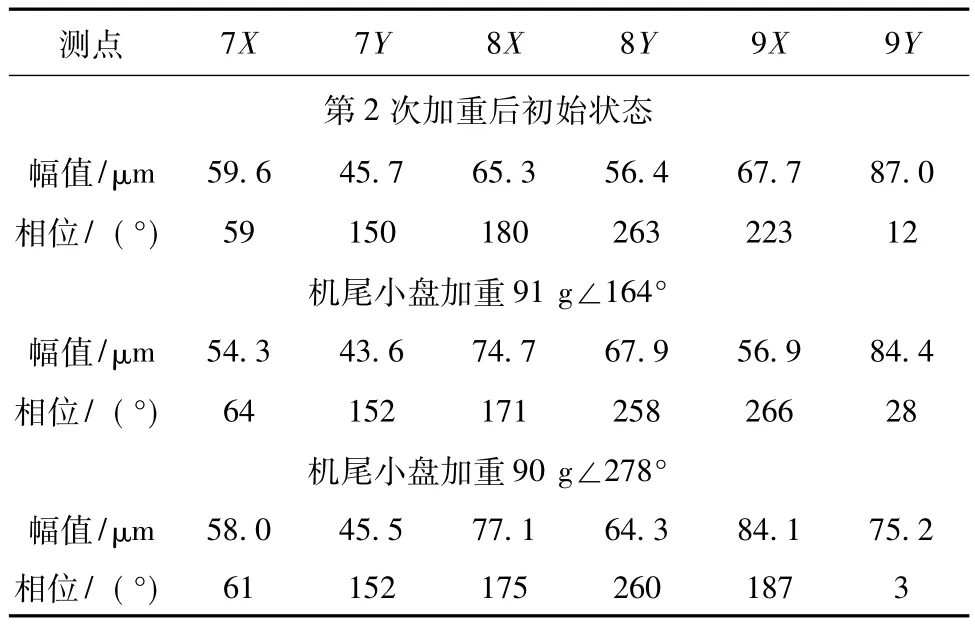
表3 后3次加重对应的工频振动值

把这3组数据两两组合，可以求出3组影响系数，计算结果见表4。

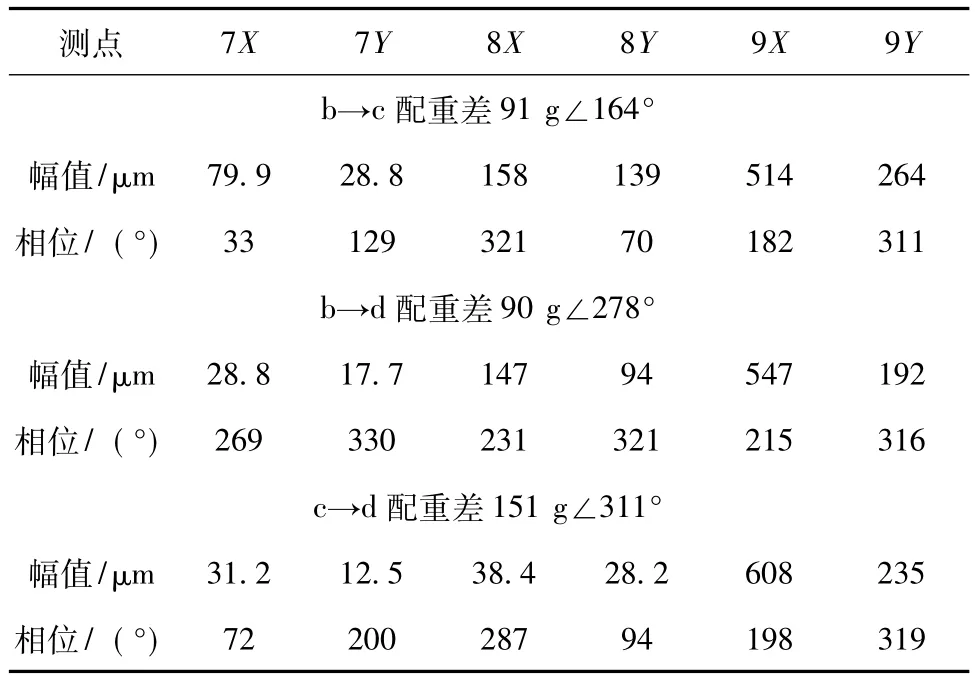
表4 机尾小盘加重的影响系数

4 影响系数分析

求出影响系数后，对计算结果进行分析，剔除不合理数据。

由表4可知，机尾小盘加重后7号瓦、8号瓦影响系数的幅值和相位都比较分散，差别很大。

根据影响系数计算原理，在机组轴系振幅不是很大、且轴承没有失稳的情况下，不平衡激振力与振动响应呈线性关系[6]。7号瓦、8号瓦的3组影响系数如此分散，说明选取的数据段中存在影响7号瓦、8号瓦振动的其它因素，计算结果不可靠，不能用于动平衡计算。也说明在机尾小盘加重对7号瓦、8号瓦振动影响较小。

表5 机组带负荷后工频振动数据

表6 预计平衡后机组剩余振动

表7 平衡后机组实测振动

机尾小盘加重后，9号瓦影响系数的幅值和相位比较接近，可靠性较高。

由式 (2)可知，若选取的数据存在一定误差，当作为除数试重较大时，计算结果的误差相对较小。

由表4可知，第3组数据一方面配重差较大，计算结果可靠性高;另一方面7号瓦、8号瓦的影响系数非常小，表明机组在2次运转中，发电机状态变化较小，数据可靠性高，因此这组数据的精度要高于其它2组，可用于动平衡计算。

5 平衡调整结果

机组带负荷运行后，振动发生一定程度的变化，9号瓦振动显著增大。2008年7月23日，机组负荷为509 MW，测得的振动值见表5。

经过平衡调整后，预计可大幅降低9号瓦振动，而不会显著影响7号瓦、8号瓦振动。经过动平衡计算后，确定机尾小盘加重量为180 g∠184°，加重后机组预计剩余振动见表6。

2008年8月3日，在机组停机间歇时间完成动平衡调整。机组启动后实测振动值见表7。可知实测与预测剩余振动值非常接近。由于实测振动值是通频振幅，往往含有显著的非工频成分，因此通常比工频值大。根据以往的测试数据，9X轴振中含有约20～30 μm的2倍频振动，扣除此影响后，9X轴振的工频振幅与预测值非常接近。

6 低发对轮加重对9号瓦振动的影响

在首次平衡调整中，假定低发对轮上的平衡调整对9号瓦轴振影响很小，进行2处平衡调整，现在利用振动数据来验证假定是否合理。

根据假定，认为前2次平衡调整中，9号瓦轴振变化全部是由机尾小盘平衡调整引起的，以此计算机尾小盘加重时9号瓦轴振的2组影响系数，计算结果见表8。

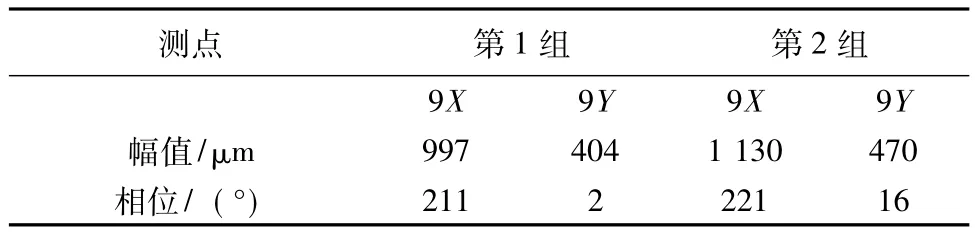
表8 含有低发对轮加重干扰的影响系数

比较表4与表8中的影响系数，可知假定低发对轮加重干扰影响很小时，计算得出的影响系数幅值和相位与机尾小盘单独加重计算得出数据有很大差别。这表明低发对轮加重会对9号瓦轴振造成很大影响，上述假定不合理，存在较大计算误差。

7 结论

a. 目前大型机组各转子之间均采用是刚性联轴器，干扰很大，假定忽略其相互影响，计算结果存在较大误差，在添加平衡试重时，应尽可能在1次平衡调整中采用单平面加重，以获得精度较高的影响系数。

b. 应选取机组工况稳定、无其它故障因素影响的数据计算，并通过对一段数据求平均数的方法尽可能控制随机误差。

c. 得到计算结果并进行分析与甄别时，首先选择加重较大的影响系数，其可靠性更高。如果在同一平面几次加重后计算所得的影响系数相差很大，应注意试验中是否存在其它显著影响振动的故障。该加重平面对要处理的测点振动影响较小，应考虑更换加重平面。

[1]施维新.汽轮发电机组振动及事故[M].北京:中国电力出版社，1998.

[2]陆颂元.汽轮发电机组振动 [M].北京:中国电力出版社，2000.

[3]张学延.汽轮发电机转子外伸端质量不平衡引起的振动分析 [J].热力发电，2004，33(10):55－58.

[4]钟一谔，何衍宗，王 正，等.转子动力学 [M].北京:清华大学出版社，1987.

[5]费业泰.误差理论与数据处理[M].北京:机械工业出版社，2004.

[6]陆颂元.大型汽轮发电机组现场高效动平衡的策略与技巧[J].中国电力，2002，47(3):1－5.