SIFT特征匹配的辐射畸变图像相对校正新方法
周可,秦世引
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
SIFT特征匹配的辐射畸变图像相对校正新方法
周可,秦世引
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
针对常规相对辐射校正方法对未配准的主从图像对校正效果欠佳的问题,在分析了辐射畸变图像的成因与特点以及相对校正的优势之后,提出了一种基于SIFT特征匹配的相对辐射校正算法.从SIFT特征的不变性出发,分别提取主从图像对的SIFT特征并进行匹配,对匹配点的灰度值进行最小二乘回归分析,得到线性变换系数,最后通过线性变换得到校正结果.实验结果表明,此方法能够有效地减小未配准主从图像对之间的辐射差异,并在复杂光照环境下的光流场计算中得到成功的应用.
未配准主从图像对;尺度不变特征变换;特征匹配;相对辐射校正;光流场
辐射畸变是指传感器在接收来自目标的电磁波辐射能时,由于电磁波在大气层中传输和传感器测量中受到传感器本身特性、光照条件等因素的影响,导致传感器测量值与目标实际的光谱辐射率不一致[1-2]的现象.实际成像过程中,普遍存在着由于光照条件等原因引起的不同时相图像间存在辐射畸变的现象.辐射畸变的存在导致许多图像不能应用于图像识别、目标检测与跟踪中,为了更好地利用目标在不同时相图像上的信息,需要对多时相图像进行辐射校正.
辐射校正是指消除同一目标在不同时相图像之间辐射畸变的过程[3].目前,辐射校正方法主要分为绝对辐射校正和相对辐射校正两大类.
绝对辐射校正方法处理时需要利用图像获取时的一些参数(例如大气能见度、太阳天顶角和传感器标定参数等),获取这些参数代价昂贵,尤其对于部分历史存档数据,获取这些参数更是不可能的.由于绝对辐射校正时需要图像获取时的参数,所以一部分卫星或航空摄影设备能够在获取图像时通过传感器记录太阳天顶角等参数,将这些参数一起传回地面保存,为图像的绝对辐射校正准备数据.
相对辐射校正是将一幅图像作为参考图像(基准图像或主图像),调整待校正图像(从图像)的灰度值,使得2幅图像上同一目标具有相同或相近的灰度分布.主图像与从图像组成一组主从图像对.相对辐射校正操作简单,且不需要图像获取时的参数.如何从不同时相的图像中准确确定同一目标的位置是相对辐射校正中的一个挑战性问题.针对这一问题,目前的解决途径是通过将主从图像对进行精确的几何配准,然后通过图像之间的坐标关系来确定目标位置.当主从图像对之间的几何配准精度偏低或未进行几何配准时,常规的相对辐射校正算法在扩大或缩小从图像的灰度分布范围的同时,会导致图像的直方图与主图像直方图有较大差异,从而导致校正效果变差.
由SIFT特征[4]的不变性可知,2幅图像上SIFT特征的匹配点在实际场景中为同一点.因此,可以通过SIFT特征提取与匹配来确定不同图像中同一目标的位置.本文提出了一种基于SIFT特征匹配的相对辐射校正算法,首先通过对主从图像对进行SIFT特征提取与匹配来进行样本点选择,再利用这些样本点进行线性相对辐射校正.
1 辐射畸变图像的成因和特点
成像过程中,输出亮度值是传感器对进入传感器的辐射能量的响应.通常,传感器正常工作在线性区,即输出亮度值与进入传感器辐射能量成正比关系.
式中:DN表示传感器的输出亮度值,DNmax表示传感器最大输出亮度值,Ls表示进入传感器的辐射值,Lmin表示传感器能够做出响应的最低辐射值,Lmax表示传感器的饱和辐射值.
在成像过程中,传感器接收到辐射能量主要有3种途径:1)光源发出的辐射能量经过目标表面反射之后进入传感器;2)部分辐射能量经过多次散射之后通过目标反射进入传感器;3)部分辐射能量不经过目标反射直接进入传感器如图1所示.

图1 辐射畸变的成因Fig.1 The formation cause of radiometric distortion
由于散射和吸收等原因,光源发出的入射辐射能量E0在照射到目标表面之前的传播过程中会发生衰减,在目标表面发生漫反射之后,进入传感器之前也会发生衰减.因此,有由光源发出的经过目标表面反射之后进入传感器的辐射能量:

式中:L1表示进入传感器的辐射能量,R表示目标表面的反射率,S表示与系统有关的系数,θ为入射角,Tθ为与入射角有关的透过率,Tφ为与反射角有关的透过率,E0为入射的辐射能量.
部分辐射能量ED经过散射之后通过目标反射进入传感器,用L2表示.

除了上述2部分辐射能量之外,还有部分辐射能量不通过目标反射而直接进入传感器,这部分能量通常称为程辐射,用Lp表示.
因此,进入传感器的总辐射能量:

在2个不同时相上获取图像时,

式(1)经过变换,可以得到Ls1与Ls2的关系如下:

在不同时相获取图像时,除了目标表面反射率R能够保持基本不变之外,其余参数都有可能发生变化,从而导致目标上同一点在不同时相图像上亮度不一致,造成辐射畸变.
从辐射畸变图像的成因可以看出,在考虑环境光照变化引起的辐射畸变时,对于不同时相的辐射畸变图像,由于相对运动的原因,同一物体上同一点的坐标关系会比较复杂,但是其灰度值满足线性关系.
2 相对校正的优势与必要条件
相对辐射校正方法按照其数学基础可分为非线性校正法和线性校正法[5-6].直方图匹配 (HM)法[7-8]是一种典型的非线性相对辐射校正方法,通过将从图像与主图像进行直方图匹配,使主从图像对具有相近的灰度概率分布,以达到减小主从图像对之间辐射差异的目的.线性相对辐射校正方法[5,9]中,同一目标在不同时相图像上灰度值满足线性关系,x和y分别表示主图像与从图像上像素的灰度值:

式中:a、b为线性方程的增益和偏移量.可通过最小二乘回归等方法估计式(2)中的参数a、b,并对从图像进行线性变换,以求得校正结果.
与绝对辐射校正相比,相对辐射校正时需要的仅仅是同一目标不同时相的图像组成的主从图像对,而不需要图像获取时的诸多参数.因此,相对辐射校正的成本低,可操作性强,给定主从图像对之后,能够自动进行辐射校正,无需人工干预.
进行相对校正时必须输入合适的主从图像对,要求目标在主从图像对上的姿态基本保持一致,目标可以在像平面内发生平移和旋转,但是不能有滚动.
3 SIFT特征提取与匹配
SIFT是一种对图像尺度变化和旋转的不变量[10-13].在构造 SIFT 特征时进行一些特殊处理,可使SIFT对图像的复杂变形和光照变化也具有较强的适应性.同时SIFT运算速度比较快,定位精度比较高.在主从图像对未进行配准时,目标可能存在平移旋转以及尺度变化,利用SIFT特征的不变性,可以很好地找到同一目标点在不同时相图像上的位置.
3.1 SIFT特征提取
3.1.1 尺度空间极值点检测与精确定位
一般而言,在合理的假设之下,尺度空间核可表示为高斯函数.设尺度因子σ可变的高斯函数为G(x,y,σ),对于图像I(x,y)而言,其尺度空间函数L(x,y,σ)可定义为如下的卷积形式[4],即


为了有效检测出尺度空间中的关键点,可用2个尺度邻近的高斯函数(为简便计,可分别取为σ和kσ)之差与待检图像进行卷积,则有

式(3)表明,此检测策略可以通过尺度空间函数L(x,y,σ)求差来实现.对于某一关键点而言,考虑尺度维因素,需要将该关键点与同一尺度下周围8邻域的像素以及相邻尺度上下对应位置的9×2=18邻域的像素,总共26个像素进行比较.
在获得大量候选特征点的基础上,通过拟合三维二次函数精确确定关键点的位置和尺度,同时去除低对比度的关键点和不稳定的边缘响应点,以增强匹配稳定性,提高抗噪声能力.
3.1.2 确定关键点方向
利用关键点邻域像素的梯度方向分布特性,为每个关键点指定方向参数,使算子具有旋转不变性.特征点(x,y)处梯度模值和方向的计算公式为

式中:L所用的尺度为关键点所在尺度.为增强梯度计算的稳定性,计算以特征点为中心邻域窗口内的梯度直方图.梯度直方图峰值处为该特征点处邻域梯度的主方向.
3.1.3 描述关键点
在以关键点为中心的16×16的窗口内,分别计算每个像素梯度的模值mij和方向θij,然后用高斯窗口对其进行加权运算,每个像素对应一个向量,长度为G(σ',i,j)*mij,G(σ',i,j)为该像素点的高斯权值,方向为θij,每个向量在4×4的子窗口范围内投影到8个梯度方向上,绘制每个梯度方向的累加值,即可形成一个8维向量.这样每个特征点就用4×4×8=128维向量来表征.最后对特征向量归一化,去除光照影响.于是,每一个关键点可以用一个128维的SIFT特征来描述.
3.2 SIFT特征匹配
进行SIFT特征匹配时,可以用2个关键点特征向量的欧氏距离作为其相似性测度.2幅图像I和I'中特征点Ii和Ij'的相似性测度为

式中:i和j分别表示2个图像中的特征点标号,F(Ii)m和F()m分别表示特征点Ii和Ij'对应的特征向量.当2个向量的欧氏距离小于阈值时认为这2个点已经匹配上.
4 基于SIFT特征匹配的相对校正策略新方法
4.1 基于SIFT特征匹配的相对辐射校正策略与算法流程
结合SIFT特征的不变性,可以利用目标上点的SIFT特征来进行样本点的选择.首先将不同时相图像上目标的SIFT特征进行匹配,取匹配点作为样本点.然后利用样本点的灰度值进行线性回归,估计线性参数.最后对从图像进行线性变换从而得到校正结果.算法的流程如表1所示.

表1 基于SIFT特征匹配的相对辐射校正算法Table 1 Relative radiometric correction method based on SIFT feature matching
4.2 算法流程的技术实现
4.2.1 样本点选择
在常规线性相对辐射校正方法中,由于其假设主从图像对已经进行了几何配准,所以在选择样本点的过程中,使用了像素点的位置信息和亮度信息.比如,图像回归法(image regression,IR)[9]将主从图像对上所有的像素都作为样本点.伪不变特征法(pseudo-invariant feature,PIF)[14-15]选择样本点的评价标准是:

式中:x(i,j)与y(i,j)分别代表主图像与从图像上像元灰度值,T1和T2为阈值.这些方法在主从图像对未进行精确配准时,选择的样本点将不符合要求,导致常规线性校正方法不适用于未配准主从图像对之间的相对辐射校正.
为了使样本点选择与主从图像对之间的配准精度无关,本文提出了一种基于SIFT特征匹配的样本点选择算法.分别对主图像和从图像提取SIFT特征,然后利用得到的SIFT特征进行特征匹配.对于能够匹配的点,认为它们是实际场景中的同一点.通过SIFT特征描述得到匹配点的坐标之后,将这些匹配点作为样本点,然后将样本点的灰度值输出,用于估计线性参数.算法流程如表2所示.

表2 基于SIFT特征匹配的样本点选择Table 2 Algorithm of sample selection based on SIFT feature matching
4.2.2 线性关系的参数估计
本文通过最小二乘回归法[16-19]来估计线性回归系数,该方法操作简单,实用性强.样本点灰度值数据集A表示为A1(x1,y1),A2(x2,y2),…,An(xn,yn),xi与yi分别代表主图像与从图像上样本点的灰度值,满足线性回归关系:

式中:代表从图像上第i个样本点灰度值的计算值.由最小二乘回归分析法可以得到

4.2.3 基于线性变换的校正结果求解
在获得线性变换参数a和b之后,对从图像进行线性变换,即可得到校正结果.线性关系为

式中:y'(i,j)为校正结果上像素(i,j)的灰度值,
y(i,j)为从图像上像素(i,j)的灰度值.
4.3 实验与评价
4.3.1 校正效果主观评测
视觉效果是评判相对辐射校正效果的最直接方法.为了便于比较,特将主图像与各种辐射校正方法对从图像的处理结果进行配准.仿真实验中,主从图像之间只存在几何位置的旋转、平移变换、灰度值的线性变换等.对于这类图像的几何配准问题,P.Vandewalle[20]提出了一种基于傅里叶频谱的配准方法.该方法将图像变换到频域,通过计算2幅图傅里叶频谱之间的相位相关性来计算旋转角,进行旋转补偿之后再计算平移向量,具有计算简单、速度快、精度可控的特点.本文选择该方法对辐射校正前的从图像及其校正结果与主图像进行几何配准.
1)高精度几何配准的辐射校正实验结果.
由于几何配准精度对传统方法的校正效果影响较大,所以先考虑高精度几何配准条件下本文方法与传统方法的辐射校正结果之比较.图2(a)、(b)给出了进行相对辐射校正前进行过精确几何配准的主从图像对及其直方图,(c)、(d)、(e)为各种辐射校正方法的处理结果及直方图.
从图2中可以看出,在高精度几何配准条件下,图像回归(IR)法、直方图匹配(HM)法以及本文方法都能够有效地使校正结果中像素的灰度分布接近于参考图像.


图2 几何配准后的主从图像对及处理结果Fig.2 The registration of master-slave image couple and the results of relative radiometric correction
2)几何配准精度欠佳时的实验结果分析.
图3中给出了进行相对辐射校正前的未配准的主从图像对.

图3 配准前主从图像对Fig.3 The unregistered master-slave image couple

图4 相对辐射校正实验结果及其直方图Fig.4 Experiment results of relative radiometric correction and their histograms
从图4中各灰度直方图可以看出,图像回归(IR)法、直方图匹配(HM)法以及本文方法都有效地增大待校正图像的灰度分布范围.但是图像回归法在增大灰度分布范围的同时也导致灰度直方图与参考图像有较大差异,而经直方图匹配法与本文方法处理之后灰度直方图与参考图像比较接近.从而表明本文方法能够有效消除图像之间的辐射差异,且有良好的鲁棒性.
4.3.2 校正效果客观评测
对于线性校正方法,可以通过比较各种方法在估计回归参数时的准确性来评价其相对辐射校正效果.实验中,待校正图像与参考图像之间满足式(2)所描述的线性关系,其中的系数a和b是已知的,因此可以通过比较校正时算法估计的系数a和b与真实值的误差来评价算法的准确性.
定义误差

式中:表示参数估计值,aj表示参数真实值,N表示实验样本数目.
在表3和表4中,a列和b列分别表示仿真时进行灰度调整时增益和偏移量的真实值,ai列和bi列分别表示配准精度高时图像回归(IR)法所估计的增益和偏移量,as列和bs列分别表示本文方法所估计的增益和偏移量.从表3和表4可以看出,在几何配准精度高时,本文方法的参数估计精度与图像回归法参数估计精度相似.

表3 几何配准精度高时参数a估计精度对比Table 3 Comparison of the accuracy of estimate parameter‘a’with high precision geometric registration

表4 几何配准精度高时参数b估计精度对比Table 4 Comparison of the accuracy of estimate parameter‘b’with high precision geometric registration
表5和表6中,a列和b列分别表示仿真时进行灰度调整时增益和偏移量的真实值,ai列和bi列分别表示几何配准误差较大时图像回归(IR)法所估计得到的增益和偏移量,as列和bs列分别表示本文方法在几何配准误差较大时所估计得到的增益和偏移量.从表5和表6可以看出,当几何配准的误差较大时,图像回归法估计的参数精度迅速下降,而本文方法的参数估计误差明显小于图像回归法,参数估计精度高.

表5 几何配准精度欠佳时参数a估计精度对比Table 5 Comparison of the accuracy of estimate parameter‘a’with low precision geometric registration

表6 几何配准精度欠佳时参数b估计精度对比Table 6 Comparison of the accuracy of estimate parameter‘b’with low precision geometric registration
均方根误差(RMSE)可用于检验图像之间的相似性,

式中:y'(i,j)与y(i,j)分别表示2 幅图像上像素(i,j)灰度值.RMSE值越小,说明参与计算的2幅图像越相似.进行RMSE计算之前,对各图像进行了几何配准.
由表7可知,校正结果与参考图像之间的RMSE值均小于从图像与参考图像之间的RMSE值,说明各算法都能有效地减小主从图像对之间的辐射差异,改善从图像与主图像的相似性.本文方法校正结果的RMSE值小于图像回归法与直方图匹配法,说明本文方法减小未配准的主从图像对之间的辐射差异的能力强于这2种传统方法.

表7 3种算法RMSE值比较Table 7 Comparison of RMSE of the processing results of three algorithms
5 复杂光照环境下面向光流场计算的校正实验结果分析
光流[21]是指图像中灰度模式的运动速度,表征了二维图像灰度变化与景物中物体结构及其运动的关系.它利用像素灰度的时域变化和相关性来确定各像素点的运动,进而分析场景中物体的结构和运动.光流场是所有光流点的集合,它是一种二维瞬时速度场,其中二维速度矢量是场景中可见三维速度矢量在成像表面上的投影.
5.1 光流原理与基本方程
Horn等人在灰度恒定假设的前提下揭示了光流的原理性定量关系,给出了光流的基本方程.他们认为在连续相邻的不同图像上,对应物上同一点的像素灰度值是相同的,此假设在连续图像序列中当灰度变化很小时近似成立.
设f(x,y,t)为t时刻在坐标(x,y)处的灰度值,u(x,y)和v(x,y)是该点光流的x和y分量.根据灰度恒定假设,在t+dt时刻,点(x,y)运动到了点(x+dx,y+dy),根据前述假设有

将式(6)的左边用Taylor级数展开得
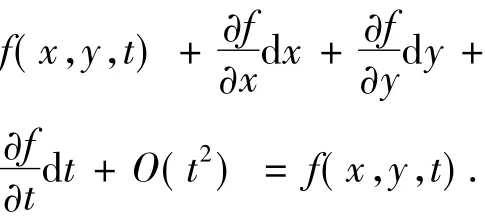
整理化简并去除无穷小可得

5.2 光流计算实验与分析
目标检测与跟踪是光流的一个重要应用.光流准确性对目标检测和跟踪的效果有显著影响.在通常的光流计算中,假设目标的灰度保持不变.然而,在实际应用中,由于遮挡、多光源、透明性以及噪声等多方面的原因,使得灰度守恒的假设条件不能满足.因此,计算得到的光流不够准确,误差过大,不能满足目标检测与跟踪的要求.图5为在环境光照变化剧烈时相邻2帧图像直接进行光流计算得到的光流图.从中可以看出,光流的分布比较混乱,误差较大,不宜用于目标检测与跟踪.

图5 辐射校正前的光流场Fig.5 The optical flow field before radiometric correction
经过对图5的分析可知灰度恒定假设是进行光流计算的一个重要前提.实际环境中拍摄到图像序列中相邻2帧图像之间不仅存在灰度分布的差异,几何位置也会存在差异.由于本文方法能够在存在几何差异的情况下对主从图像对进行有效的辐射校正,因此,选择本文方法对输入的图像序列进行辐射校正,从而使前后2帧图像中目标的亮度保持基本不变,适合于进行光流计算.
图6(a)、(b)为使用本文方法进行辐射校正之后的光流计算结果.从图中可以看出,进行辐射校正之后计算出的光流比校正前计算的光流更合理,可以应用于目标检测与跟踪中.

图6 辐射校正后的光流场Fig.6 The optical flow field after radiometric correction
6 结束语
本文对常规相对辐射校正方法中的图像回归法进行了改进,采用基于SIFT特征匹配的方法进行特征点选择,通过线性回归的方法求解线性参数之后对从图像进行线性变换得到校正结果.实验表明,在主从图像对之间的几何配准精度偏低时,本文方法的处理效果优于图像回归法以及直方图匹配法.将该方法应用于复杂环境下的光流场计算的问题中,很好地解决了由于光照变化导致的光流场计算错误问题,验证了本算法的处理效果.
[1]汤国安,张友顺,刘永梅,等.遥感数字图像处理[M].北京:科学出版社,2004:104-123.
[2]JENSEN J R.Introductory digital image processing a remote sensing perspective[M].3rd ed.Beijing:China Machine Press,2007:152-236.
[3]贺威.传感器与遥感影像的辐射校正方法探索[D].秦皇岛:燕山大学,2005:1-24.
HE Wei.The research of radiometric correction of sensor and remoto sensing images[D].Qinhuangdao:Yanshan university,2005:1-24.
[4]LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[5]朱绍攀,陈宇.大气辐射校正方法分析[J].地理空间信息,2010,8(1):113-116.
ZHU Shaopan,CHEN Yu.Methods for atmospheric radiation correction[J].Geospatial Information,2010,8(1):113-116.
[6]DENG Shubin,WU Honggan,JIANG Tao.A study on relative radiometric normalization for remote sensing dynamic monitoring[J].Remote Sensing Information,2008,4:71-75.
[7]张鹏强,余旭初,刘智.多时相遥感图像相对辐射校正[J]. 遥感学报,2006,10(3):339-344.
ZHANG Pengqiang,YU Xuchu,LIU Zhi.A study on relative radiometric correction of multitemporal remote sensing images[J].Journal of Remote Sensing,2006,10(3):339-344.
[8]吴文瑾.使用VC实现基于直方图的相对辐射校正[J].电脑知识与技术,2009,5(12):3202-3203,3206.
WU Wenjin.Relative radiometric correction with VC program based on histogram matching method[J].Computer Knowledge and Technology,2009,5(12):3202-3203,3206.
[9]丁丽霞,周斌,王人潮.遥感监测中5种相对辐射校正方法研究[J]. 浙江大学学报,2005,31(3):269-276.
DING Lixia,ZHOU Bin,WANG Rencao.Comparison of five relative radiometric normalization techniques for remote sensing monitoring[J].Journal of Zhejiang University,2005,31(3):269-276.
[10]王田甲,刘国荣.SIFT改进算法在图像配准中的应用[J].微电子学与计算机,2011,28(5):184-188.
WANG Tianjia,LIU Guorong.Improved SIFT algorithm for image matching[J].Microelectornics & Computer,2011,28(5):184-188.
[11]于丽莉,戴青.一种改进的SIFT特征提取算法[J].计算机工程,2011,37(2):210-212.
YU Lili,DAI Qing.Improved SIFT feature matching algorithm[J].Computer Engineering,2011,37(2):210-212.
[12]付永庆,宋宝森,吴建芳.边缘分类SIFT算法[J].哈尔滨工程大学学报,2010,32(5):632-636.
FU Yongqing,SONG Baosen,WU Jianfang.An improved scale invariant feature transform algorithm[J].Journal of Harbin Engineering University,2010,32(5):632-636.
[13]李萍,周荣福,刘苗.柱面全景图单点投影及配准拼接算法[J]. 自动化技术与应用,2011,30(3):36-39,60.
LI Ping,ZHOU Rongfu,LIU Miao.One-point projection and registration of cylinder panorama[J].Techniques of Automation and Applications,2011,30(3):36-39,60.
[14]郭丽峰,高小红,亢健,等.伪不变特征法在遥感影像归一化处理中的应用[J].遥感技术与应用,2009,24(5):588-595.
GUO Lifeng,GAO Xiaohong,KANG Jian,et al.Application of the pseudo-invariant feature in normalization process of the remote sensing images[J].Remote Sensing Technology and Application,2009,24(5):588-595.
[15]SCHOTT J R,SALVAGGIO C,VOLCHOK W J.Radiometric scene normalization using pseudo-invariant features[J].Remote Sens Environ,1988,26:1-16.
[16]SLEPIAN D.Linear least-squares filtering of distorted images[J].Opt Soc Amer,1967,57(7):918-922.
[17]李福金,秦志伟.最小二乘影像匹配算法设计与实现[J]. 测绘与空间地理信息,2011,34(2):190-192.
LI Fujin,QIN Zhiwei.Design and implementation of the algorithm of least squares image matching[J].Geomatics& Spatial Information Technology,2011,34(2):190-192.
[18]邱卫宁,齐公玉,田丰瑞.整体最小二乘求解线性模型的改进算法[J].武汉大学学报,2010,35(6):708-710.
QIU Weining,QI Gongyu,TIAN Fengrui.An improved algorithm of total least squares for linear models[J].Geomatics and Information Science of Wuhan University,2010,35(6):708-710.
[19]BIDAY S,BHOSLE U.Relative radiometric correction of cloudy multitemporal satellite imagery[J].World Academy of Science,Engineering and Technology,2009,51:241-245.
[20]PATRICK Vandewalle.Super-resolution from unregisted aliased images[D].Brussels,Belgium:Katholieke Universiteit Leuven,2006:31-37.
[21]HUANG Yan,ZHUANG Xinhua.Optic flow field segmentation and motion estimation using a robust genetic partitioning algorithm[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(12):1177-1190.

周可,男,1986年生,硕士研究生,主要研究方向为混叠序列图像校正与超分辨率重建.

秦世引,男,1955年生,教授,博士生导师,主要研究方向为复杂系统的智能控制、图像处理与模式识别等.作为负责人主持完成(或在研)国家攀登计划项目的子课题、国家“973”计划项目的子课题、国家“863”计划项目、国家自然科学基金项目、国防科技预研基金项目等20余项.1999年获全国优秀科技图书奖暨科技进步奖(科技著作)一等奖,1999年获国家第5届工程设计优秀软件金奖.发表学术论文180余篇,出版学术专著1部,研究生教材1部,译著2部.
A novel method for relative correction of a radiometric distortion image based on SIFT feature matching
ZHOU Ke,QIN Shiyin
(School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China)
In view of the issue of traditional relative radiometric correction methods not being able to handle the effects in dealing with unregistered master-slave image couples,systematic analysis of formation causes and radiometric distortion image characteristics was carried out and the advantages of relative corrections were investigated.Therefore,a novel relative radiometric correction method was proposed based on SIFT feature matching.Depending on their feature invariance,the SIFT features of the master-slave image couple were extracted and matched first,and then the least square regression was employed to analyze the gray values of the matching points in order to obtain the linear transformation coefficients.Finally the correction result was achieved through the linear transformation of the slave image.A series of experimental results show that the radiometric differences between the unregistered master-slave image couples may be effectively reduced by using this method.In addition,this method has been successfully applied in the calculation of an optical flow field under complex light environments.
unregistered master-slave image couple;scale-invariant feature transform;feature matching;relative radiometric correction;optical flow field
TP751
A
1673-4785(2011)06-0507-08
10.3969/j.issn.1673-4785.2011.06.005
2011-07-07.
国家自然科学基金资助项目(60875072);北京市自然科学基金资助项目(4112035);中澳国际合作资助项目(2007DFA11530).
周可.E-mail:freehawkzk@126.com.

