基于Matlab的Kalman滤波教学实践

占荣辉，鲁 敏

(国防科技大学电子科学与工程学院，湖南长沙 410073)

0 引言

雷达、声纳、导航、通信和自动控制等诸多应用中，需要对一个随机动态系统的状态进行估计，由一个测量装置对系统状态进行测量，通过记录的测量值对状态进行最优估计。对于平随机稳过程，Wiener滤波器可得到线性系统状态的最优(最小均方误差意义下)估计;而对于非线性系统或非平稳环境，Wiener滤波却不再适用。对于线性系统，只要噪声是高斯型的，通过Kalman滤波总就能得到状态的最优估计，且这种估计过程是递推进行的;即便是对于非线性系统，Kalman滤波器的扩展形式仍能适用于状态估计(此时可能是次优的)［1，2］。由于 Kalman 滤波在系统状态估计、参数估计以及状态—参数联合估计等方面应用的广泛性和表现出的突出优势，在高年级本科生或研究生开设的“统计信号处理”、“随机信号处理”和“自动控制”或其它相关课程中都将其列为重点内容进行讲解。

但是，Kalman滤波器的推导和应用涉及的数学理论强，概念抽象，且涉及到大量复杂的矩阵运算，在实际教学中学生往往感觉这一知识点晦涩难懂，对其中的分析方法和基本理论不能很好地理解与掌握。单纯通过公式的机械记忆很难正确领会问题的本质，更谈不上将Kalman滤波方法应用于解决实际问题。Matlab集数值运算、矩阵运算、符号运算和图形处理等功能于一体。且具有涵盖多个专业领域的工具箱函数，因此利用该软件可以方便地建立系统数学模型，使得许多繁琐的计算与图形绘制等工作被简单的软件包或函数调用操作所代替［3－5］。

1 Kalman滤波方程推导

本文从最优Bayes估计的理论公式出发导出Kalman滤波算式，可望从另一个角度对Kalman滤波方法作更直观的解释，同时拓宽学生的思维。

考虑下列方程所描述的线性系统:

其中，xk为系统状态(m维列向量);F为从k－1时刻到k的状态转移矩阵;H为观测矩阵;wk和vk分别为m维和n维零均值过程噪声和测量噪声。

从Bayes估计的观点看，滤波问题就是在给定观测y1:k={yi}的条件下得到时变状态量xk的估计，这要求建立后验状态分布 的概率密度函数PDF。假定初始PDF为p(x0|y0)=p(x0)，则理论p(xk|y1:k)可通过两步递推计算求得。

［预测］:假定k－1时刻状态的后验PDF设为p(x1:k－1)，则其一步前向预测的 PDF可以根据Chapman-Kolmogorov方程计算

［滤波:］在获得 p(xk|y1:k－1)的基础上，综合新近的观测yk，可通过如下的Bayes规则计算k时刻状态的后验PDF:

式(3)和式(4)构成了一个由k－1时刻后验PDF向k时刻后验PDF递推的过程，但这只是理论上的递推式。实际的求解过程依赖于具体的系统方程形式。若p(xk－1|y1:k－1)满足高斯分布，且wk和vk为相互独立的高斯噪声(其协方差分别Qk和Rk)，则可得到xk的最大后验估计为

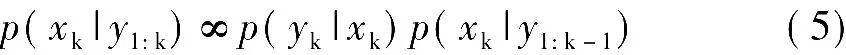
对上式取对数，得到其等价的算式为

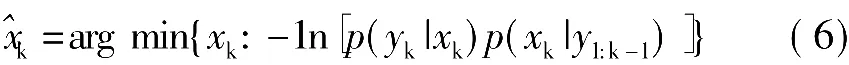
容易证明p(xk|y1:k－1)和p(xk|y1:k)可以通过解析递推求得，且满足高斯分布:

其中，

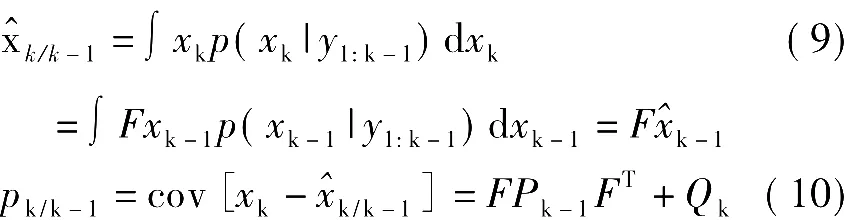
又因为

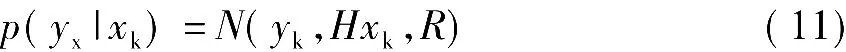
于是满足式(6)的xk等价于

对上式进一步变形，可得

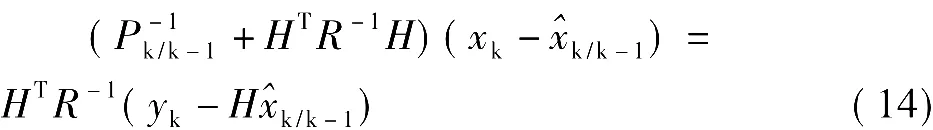
由于矩阵Pk/k－1和R均为对称下定阵，故矩阵可逆，于是由式(14)可得

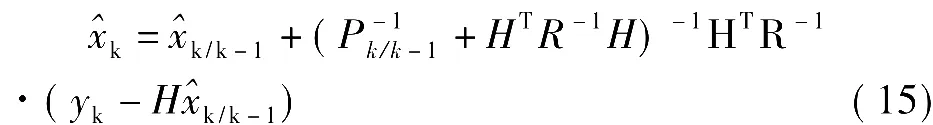
若定义

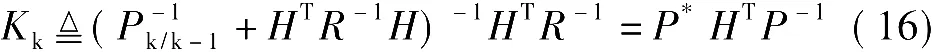
对上式进行适当的变形，可得

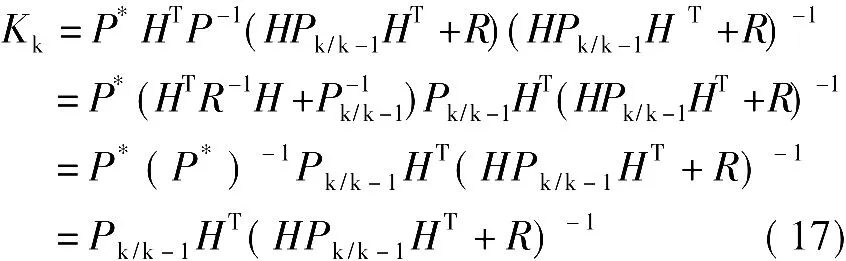
同理可得

将式(17)中的Kk代入式(18)，并采用矩阵求逆引理化简，可得

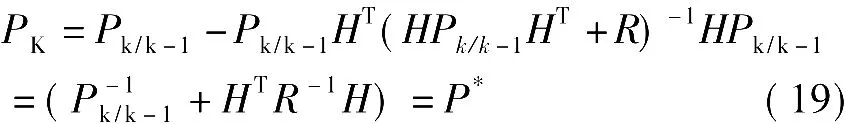
于是有

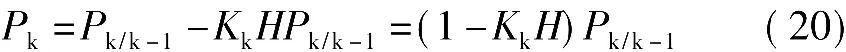
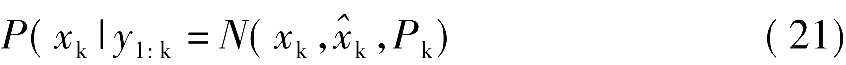
由此可得完整的Kalman滤波递推算式:

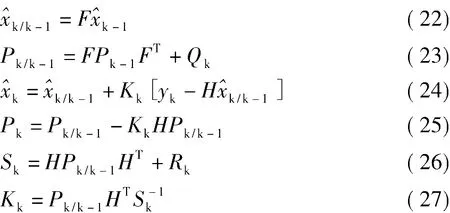
式中，Kk为卡尔曼增益，Sk为信息中vk=yk－的协方差距阵，上述结果与文献［1］中采用正交化原理导出的算式完全一致。我们只要给一的定初始条件:，通过式(22)～式(25)进行递推计算，即可动态得到状态量xk的滤波估计。

2 Kalman滤波教学实例

2.1 标量情况—状态预测

［例1］有一满足AR(1)模型的随机序列，其状态演化过程可用差分方程表示为

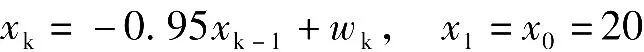
用观测方程yk=xk+vk对xk进行观测，其中的wk和vk分别是方差为Q=1和R=9的零均值高斯白噪声。试利用Kalman方程对xk进行预测，并给出状态序列测量与预测的图示结果。

假设初始状态估计及估计方差分别为^x=23和P0=9，可以得到的Matlab预测结果如图1和图2所示。

由图1和图2的结果可以看出，经Kalman滤波得到的预测精度比单纯的测量精度要高(说明了其在带噪声的测量中恢复信号的能力)。由式(22)～式(25)可知，滤波过程通过两个步骤来完成:一是预测，二是修正，即先通过式(22)和式(23)获得状态及其方差的预测，再通过式(24)和式(25)完成状态和方差的修正。且这两个步骤是交替重复进行的。状态的修正量△xk=Kkvk，故滤波结果既包含了(模型)预测的成份同时包含了测量成份，通过修正提高了估计精度，这一点在图1的结果中得到了很好的体现。

下面通过对本例的理论分析与仿真结果进行比较，来说明Kalman滤波的收敛过程。由仿真条件及式(22)～式(27)的滤波公式可知:

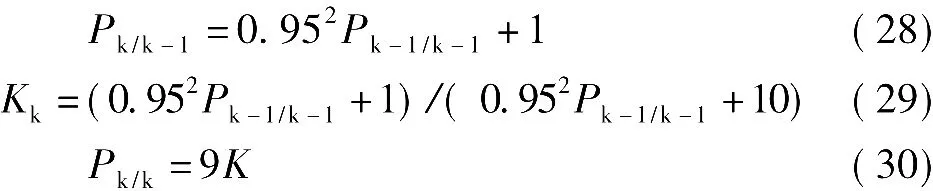
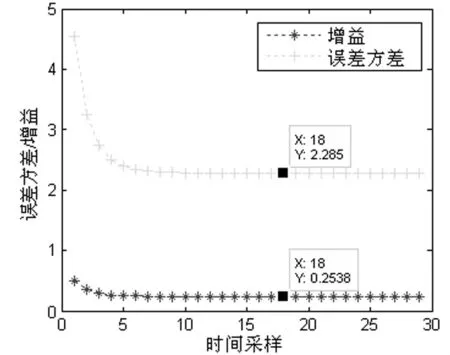
图1 Kalman滤波器预测过程

从P0/0=P0=9开始，通过式(28)～式(30)容易算出上面几个参数的理论值，如表1所示。

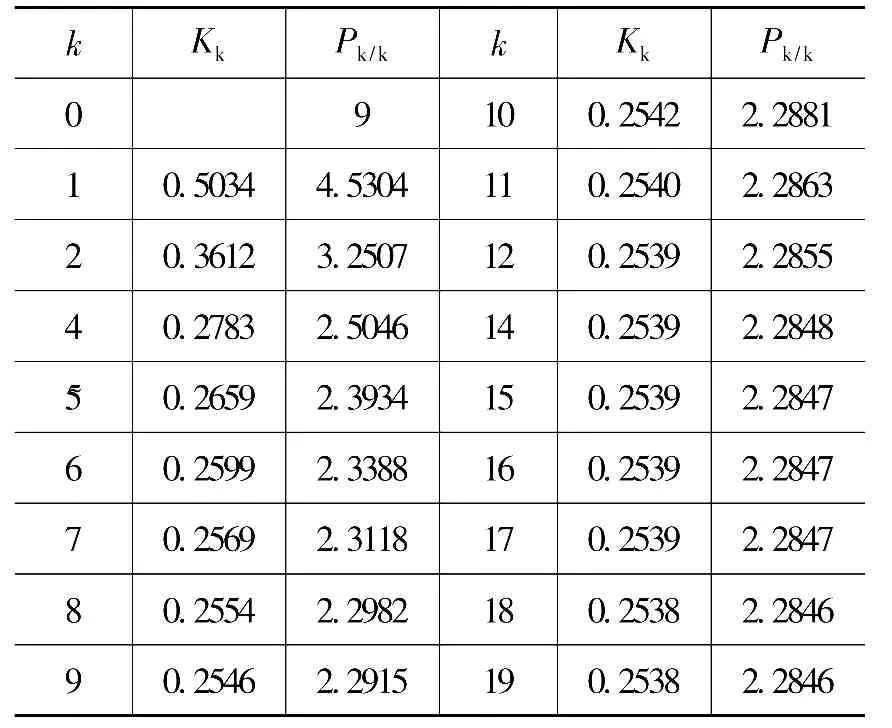
表1 误差方差与Kalman增益计算结果

若设Pk/k的稳态值(即当k→时，误差方差Pk/k趋近的稳定值)为 珔P ，则应有 Pk/k=Pk－1/k－1=珔P，进一步根据式(30)可得

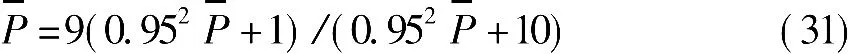
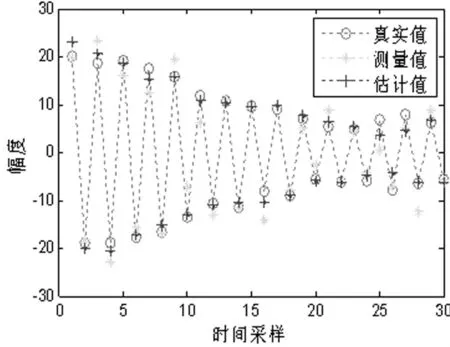
图2 误差方差和增益变化曲线

2.2 矢量情况—目标跟踪

考虑某一维坐标轴中的跟踪滤波问题，目标的运动状态可描述为

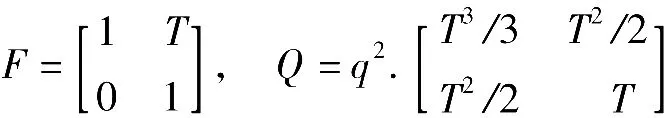
式中，T为采样间隔(观测周期)，q2为扰动噪声方差。

传感器测量方程为

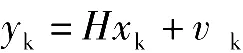
其中，H=［1 0］为测量矩阵，v∽N(0，R)为观测噪声。

［例2］目标初始位置x1=x0位于坐标原点，初始速度在［6，10］之间均匀分布，T=0.5，q=1 ，R=1。试给出目标位置的跟踪过程，并评估跟踪性能。

假设状态估计及其误差协方差矩阵采用“两点法”初始化，即具有和:

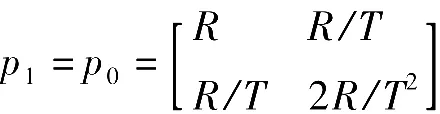
得到的Matlab目标跟踪仿真结果如图3和图4所示。

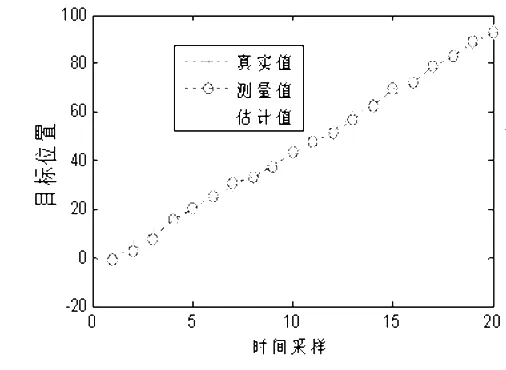
图3 目标跟踪滤波过程

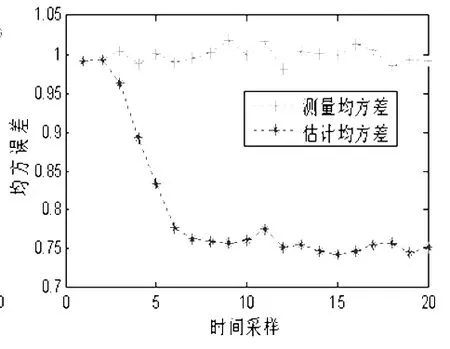
图4 目标跟踪均方差

图3和图4给出了前20个时刻目标位置的演化过程及测量与跟踪结果，这是通过5000次的Monte Carlo仿真得到的目标跟踪的性能曲线。由图中的结果可见，相比于直接测量(均方误差约为1)，通过Kalman滤波处理后，其估计精度有了较大改善(图中均方误差约为0.75)，说明了Kalman滤波在目标跟踪应用中的有效性和可行性。

3 结语

本文介绍了一种基于Matlab仿真的教学方法:我们避开了正交性原理等相关知识，从最优Bayes滤波的角度出发，导出了Kalman滤波方程;在此基础上结合两个典型的应用实例，给出了完整的Kalman滤波算法实现程序及相应的实验结果。

教学实践证明，应用Matlab仿真工具辅助的Kalman滤波教学，可以有效帮助学生加深对基本概念和基本原理的理解，将其注意力集中于对基本分析方法的掌握上，从而真正领悟解决实际问题的思路和技巧。通过可视化工具的应用，使讲授的内容形象化和具体化，有效提高了授课效率;通过具体实例的讲解和现场仿真实现，扩展了学生的思维空间，提高了学生解决实际问题的能力，改善了教学质量。

［1］ Steven M.Kay著.罗-鹏飞等译.统计信号处理基础-估计与检测理论［M］.北京:电子工业出版社，2003.

［2］ Eli Brookner.Tracking and Kalman Filtering Made Easy［M］.New York:John Wiley＆ Sons，1998.

［3］ 张刚，贺利芳，何方白等.基于Matlab的“数字信号处理”课程教学探索［J］.北京:高等教育研究，2007，24(2):45-46.

［4］ 杜世民，杨润萍.Matlab在“信号与系统”教学中的应用研究［J］.南京:电气电子教学学报，2009，31(6):89-91.

［5］ 罗军辉，罗勇江，白义臣等.MATLAB7.0在数字信号处理中的应用［M］.北京:机械工业出版社，2005.

［6］ 张旭东，陈明泉.离散随机信号处理［M］.北京:清华大学出版社，2005.