关于互易二端口的若干思考
于歆杰
(清华大学电机工程与应用电子技术系,北京 100084)
二端口网络是“电路原理”课程教学中理论性比较强的内容,公式较多,概念较多,容易出错。在笔者教学实践中,有学生问到,理想变压器的T参数满足互易二端口的条件,因此四个参数中只有三个是独立的,那如何用三个电阻构成的T型网络或Π型网络来构造其等效网络呢?这个问题乍一听,让笔者很是无措了一阵。原因在于用理想变压器的T参数来构造T型等效电阻网络或Π型等效电阻网络将获得三个无穷大电阻或0值电阻。由此引发了笔者对互易二端口定义的深入思考,形成了这篇文章。本文所有变量和参数均是在拉普拉斯变换域中讨论的。
1 关于互易二端口定义的几种方法
现行电路教材中,对互易二端口的处理方式有如下几种:
(1)根据端口外特性定义[1]。对于如图1所示的二端口来说,我们可以发现和是该二端口两对可以现实存在的支路量,如果它们之间满足
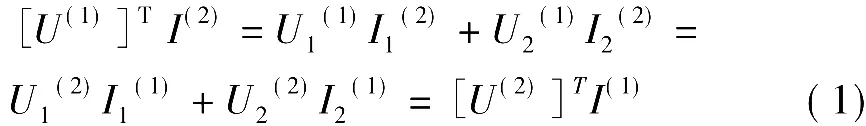
则称其为互易二端口。U(1)和I(1)被称为一对容许偶,U(2)和I(2)是另一对容许偶。
(2)根据二端口参数定义[2-4]。如果某二端口有Z参数,且Z12=Z21,则该二端口为互易二端口。类似地,还可以给出基于其余五种二端口参数的互易二端口判据。
(3)根据构成二端口网络的元件定义[5]。仅包含线性非时变电阻、电容、电感、互感和理想变压器的二端口称为互易二端口。
(4)根据互易定理定义[6,7]。满足互易定理的二端口为互易二端口。这里所指的互易定理,是指仅含线性电阻R、电感L、电容C和一个激励源构成的电路,在仅交换激励与响应的位置后,激励和响应之间构成比例关系的陈述[4,6,8,9]。
(5)对互易二端口未给出明确定义[8,9]。

图1 二端口网络
本文接下来从“互易”二字的本质出发,讨论上述各种定义之间的关系。
2 根据端口激励响应间关系定义
顾名思义,如图1所示的二端口互易性质指的是如果激励e(excitation)在端口A,响应r(response)在端口B,那么同值激励换至端口B,换至端口A的响应值不发生变化。满足互易性质的二端口称为互易二端口。这里需要指出,换至端口B的激励只不过在数值上保持不变,在激励形式上需要根据换前端口B的响应形式而定(电压响应变换为电流源激励,电流响应变换为电压源激励)。即互易的含义为:激励与响应的位置(两个端口间)与形式(电压与电流)互换后,如果激励的数值不变,则响应的数值保持不变。此外,如果响应为电压,我们总假设与其相连的二端口的入端运算阻抗为无穷大,即可用开路电压来表示响应;如果响应为电流,我们总假设与其相连的二端口的入端运算导纳为无穷大,即可用短路电流来表示响应。
如果我们假定激励的方向总是按照图中所示参考方向施加,响应的参考方向为信号和能量传递的自然方向(即电压响应上正下负,电流响应从端口流出)。则依据激励的不同形式和位置,可以有如图2所示的如下八种情况的互易二端口。

图2 互易二端口网络
1)激励e为1侧电压源,响应r为2侧短路电流(前提是2侧允许短路)。互换后,激励为2侧电压源(从1侧换至2侧,从电流响应换至电压激励),响应为1侧短路电流(从2侧换至1侧,从电压激励换至电流响应)。其前提是1侧允许短路,如图2(a)所示。
2)激励e为1侧电流源,响应r为2侧开路电压(前提是2侧允许开路)。互换后,激励为2侧电流源(从1侧换至2侧,从电压响应换至电流激励),响应为1侧开路电压(从2侧换至1侧,从电流激励换至电压响应)。其前提是1侧允许开路,如图2(b)所示。
3)激励e为1侧电压源,响应r为2侧开路电压(前提是2侧允许开路)。互换后,激励为2侧电流源(从1侧换至2侧,从电压响应换至电流激励),响应为1侧短路电流(从2侧换至1侧,从电压激励换至电流响应)。其前提是1侧允许短路,如图2(c)所示。
4)激励e为1侧电流源,响应r为2侧短路电流(前提是2侧允许短路)。互换后,激励为2侧电压源(从1侧换至2侧,从电流响应换至电压激励),响应为1侧开路电压(从2侧换至1侧,从电流激励换至电压响应)。其前提是1侧允许开路,根据图2(d)所示。
5)激励e为2侧电压源,响应r为1侧短路电流。根据图2(a),这与第1种情况相同。
6)激励e为2侧电流源,响应r为1侧开路电压。根据图2(b),这与第2种情况相同。
7)激励e为2侧电流源,响应r为1侧短路电流。根据图2(c),这与第3种情况相同。
8)激励e为2侧电压源,响应r为1侧开路电压。根据图2(d),这与第4种情况相同。
图2清晰地表明了实际可能存在的四种互易二端口。容易验证,图2中的四种互易二端口满足式(1),即第2节给出的基于端口激励响应间互易的定义满足第1节给出的基于容许偶的定义。式(1)更具普遍性,但抽象程度较高,不易理解“互易”的含义。
从本节的讨论还可以看出,具有互易性质的二端口,信号和能量从两个方向传递的性质是相同的。这一点有可能使得互易定理在实际中得到应用。
从互易的本质属性(即激励与响应在位置、形式进行互换后,如果激励保持原值,响应也保持原值)出发,也可以定义二端口的对称性。即激励的同侧响应和对侧响应在激励与对侧响应进行位置、形式的互换后且激励保持原值的前提下均保持不变。限于篇幅,这里不再赘述。
3 根据二端口参数定义
图1所示的二端口共有四个端口支路量,需要二个独立方程实现用二个支路量描述另外二个支路量,因此总共有六种方程,即Z参数、Y参数、H参数、反H参数、T参数和反T参数方程:
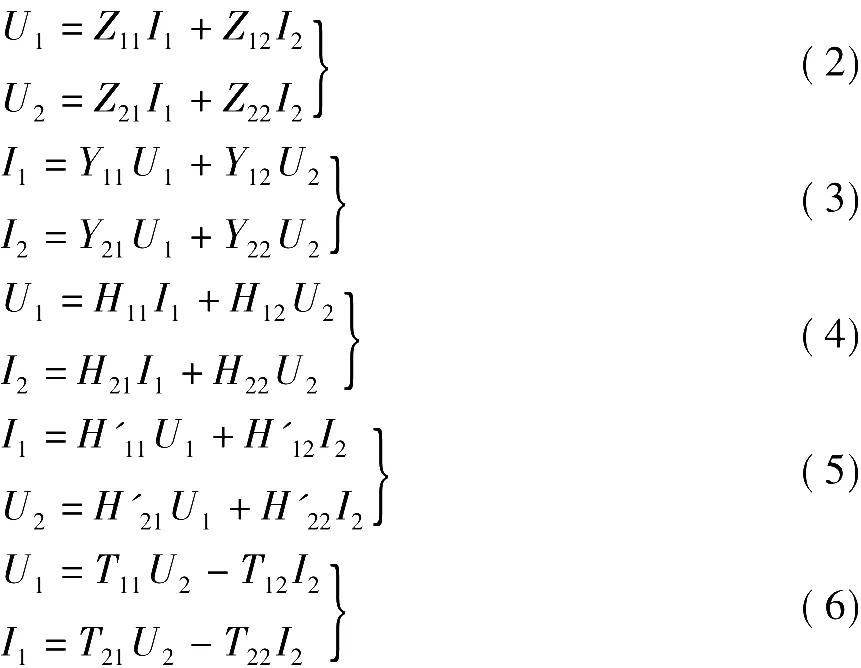

下面我们根据图2和式(2)~式(7)分别推导几种参数对应的互易条件。
1)如果二端口有Y参数,根据图2(a),可知左图2侧电路r=-I2=-Y21U1=-Y21e(U2=0),右图1侧电路r=-I1=-Y21U2=-Y12e(U1=0)。
因此具有Y参数的二端口是互易二端口的充要条件为Y12=Y21。
2)如果二端口有Z参数,根据图2(b),可知左图2侧电路r=U1=Z21I2=Z21e(I2=0),右图1侧电路r=U1=Z12I2=Z12e(I1=0)。因此具有Z参数的二端口是互易二端口的充要条件为Z12=Z21。
3)如果二端口有反H参数,根据图2(c),可知左图2侧电路r=U2=H'21U1=H'21e(I2=0),右图1侧电路r=-I1=-H'12I2=-H'12e(U1=0)。因此具有反H参数的二端口是互易二端口的充要条件为H'12=-H'21。
4)如果二端口有H参数,根据图2(d),可知右图1侧电路r=U1=H12U2=H12e(I1=0),左图2侧电路r=-I2=-H21I1=-H21e(U2=0)。因此具有H参数的二端口是互易二端口的充要条件为H12=-H21。
5)如果二端口有T参数,根据图2(d),可知左图2侧电路r=-I2=I1/T22=e/T22(U2=0),右图1侧电路 I2=T21/T22U2,r=U1=(T11-T12T21/T22)U2=(T11-T12T21/T22)e(I1=0)。具有T参数的二端口是互易二端口的充要条件为T11T22-T12T21=1。
6)如果二端口有反T参数,根据图2(c),可知右图1侧电路r=-I1=I2/T'22=Te/T'22(U1=0),左图2侧电路 I1=-T'21/T'21U1,r=U2=(T'11-T'12T'21/T'22) ,U1=(T'11-T'12T'21/T'22)e(I2=0)。因此,具有反T参数的二端口是互易二端口的充要条件为 T'11T'22-T'12T'21=1。
通过本节讨论可知,如果二端口有某种参数,则根据端口变量互易特性定义的互易二端口与根据二端口参数定义的互易二端口完全等价。以图2(b)所示的情况2和式(2)所示的Z参数为例。在讨论端口变量互易特性时,我们假设与其相连的二端口的入端运算阻抗为无穷大,因此响应可用开路电压表示。这个假设在在讨论Z参数时等价于1侧和2侧允许开路。于是可求出二端口的Z参数(开路参数),其等价的互易条件为Z12=Z21。其余可依此类推。
类似地,如果在图2中标出激励的同侧响应,结合式(2)∽式(7),也可以给出对称二端口参数的定义形式。限于篇幅,这里也不再赘述。
4 互易元件和互易二端口
电路中有些基本元件本身就是四端元件,如果其构成二端口,则根据参数可判断其是否为具有互易性质的元件。比如,理想变压器具有T参数,且满足第3节讨论的条件,因此其为具有互易性质的元件。互感具有Z参数,且满足第3节讨论的条件,也具有互易性质。
对于二端元件来说,也可以仿照第2节讨论的激励与响应互换的思想来定义其互易性质。不过在二端元件中,不存在位置的互换,只存在形式的互换。对于关联参考方向下的线性非时变电阻R来说,设激励为电流源I,响应为电压U=RI。接下来激励与响应的形式互换,即电压形式的响应换为电流形式的激励I,电流形式的激励换为电压形式的响应U=RI。显然,线性非时变电阻为具有互易性质二端元件。容易验证,零状态的线性非时变电容和电感也为具有互易性质的二端元件。不难验证,独立源和受控源不具备互易性质。
具有互易性质的元件简称互易元件,不具有互易性质的元件简称非互易元件。
有了上述基础后,即可讨论第1节中互易二端口的第3和第4种定义。这两种方法可以统一陈述为:仅由互易元件构成的二端口一定是互易二端口。之所以说该陈述包含了第4种定义,是指互易定理证明过程中(特勒根定理或回路法),势必利用该二端口内部元件的互易性质,才能得到端口变量的互易性质。事实上,图2已经给出了互易定理的四种情况。
需要指出,从构成元件和互易定理出发,并非得到互易二端口的定义,而是其充分条件。如图3所示的二端口包含非互易元件(受控源),不满足互易定理,但由于其Y参数矩阵满足Y12=Y21因此为互易二端口。
可以将互易二端口的几种定义方式总结如下:
方式(1):根据端口变量的互易特性定义。一般性的表述为式(1),有明确互易行为(前提是响应端口能够被开路或者短路)的表述见第2节。此为互易二端口的充要条件。

图3 含非互易元件、不满足互易定理的互易二端口
方式(2):如果二端口有某种参数,则该参数的互易条件与方式(1)等价。此亦为互易二端口的充要条件。
方式(3):由互易元件构成的二端口是互易二端口。满足互易定理的二端口是互易二端口。这两个陈述均为互易二端口的充分条件,即确定的为互易二端口的一个子集。图3所示电路即为包含非互易元件、不满足互易定理的互易二端口。
5 几组相互关联的概念
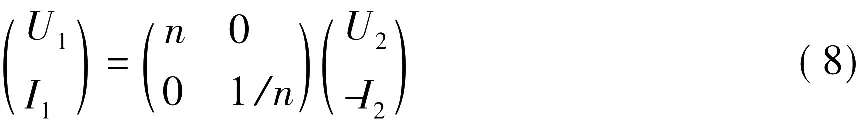
易知,其满足第3节讨论的条件,即理想变压器是互易元件(或互易二端口)。但引言部分提出的问题在以下几个方面存在概念性缺陷:
(1)根据互易定理,由线性非时变电阻构成的二端口一定是互易二端口,但反之不一定成立,即互易二端口不一定由线性非时变电阻构成;
(2)理想变压器本身的参数仅有一个n,而非常规互易二端口的三个独立参数;
(3)理想变压器本身是基本电路元件。关于互感和理想变压器是否电路基本元件,学界认识不尽相同。本文采用互感和理想变压器是电路基本元件这一说法。如果能够用电阻元件构成的网络来替代其外特性,其不可能为电路基本元件。
最后还需要区分一下无源二端口和互易二端口。所谓无源二端口,是指在图1所示参考方向下,设端口电压电流在-∞时为0,对任意的t值均有
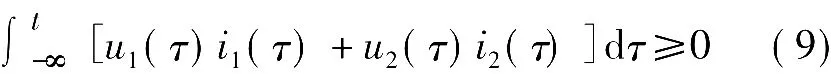
回到本文一开始的问题中来,对于理想变压器来说,有T参数方程(以同名端在同侧为例):
此处端口变量为时域值。
回转器有Z参数方程:
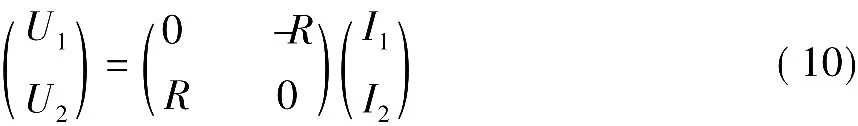
代入式(9)中被积部分得

因此回转器为无损元件,当然是无源元件。但是根据第3节的讨论可知,其为非互易元件。也就是说,无源二端口不能导出互易二端口。
反过来,互易二端口也不能导出无源二端口。
[1] 肖达川.线性与非线性电路[M].北京:北京科学出版社,1992
[2] [美]狄苏尔,葛守仁著,林争辉译.电路基本理论[M].北京:北京人民教育出版社,1979
[3] [美]James Nilsson and Susan Riedel.Electric Circuits(7th)[M].Pearson,2005
[4] 于歆杰,朱桂萍,陆文娟.电路原理[M].北京:北京清华大学出版社,2007
[5] 李瀚荪.简明电路分析基础[M].北京:北京高等教育出版社,2002
[6] 周守昌.电路原理(第2版)[M].北京:北京高大学等教育出版社,2004
[7] 周庭阳.n端口网络[M].北京:北京高等教育出版社,1991
[8] 江缉光.电路原理[M].北京:北京清华大学出版社,1997
[9] 邱关源.电路(第四版)[M].北京:北京高等教育出版社,1999

