两种三相电路总视在功率计算公式的关系

李自成，谭延良，周新云，赵不贿

(江苏大学电气信息工程学院，江苏镇江 212013)

三相电路的有功功率、无功功率和视在功率是“电工技术”课程的一个重点内容，而三相电路总视在功率的计算则存在争议。下面是一道关于三相电路总视在功率计算的非电类专业大学本科考试的选择题。

［选择题］三相电路如图1所示。在下列式子中，表示三相负载总视在功率的为()。

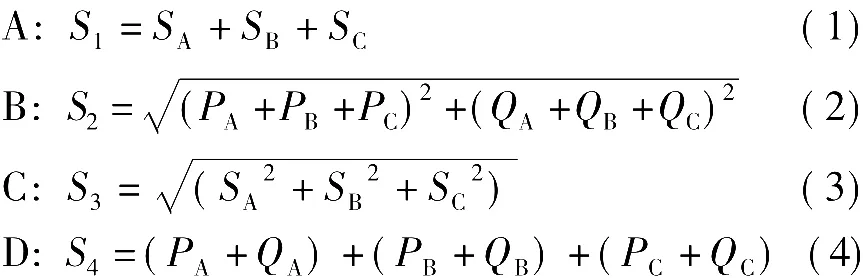
本文从此题入手，探讨了S1和S2之间的关系。

图1 负载星形连接的三相三线制电路

1 三相电路总视在功率的计算

1.1 三相电路的有功、无功和视在功率

根据文献［1］，三相电路的总有功功率为

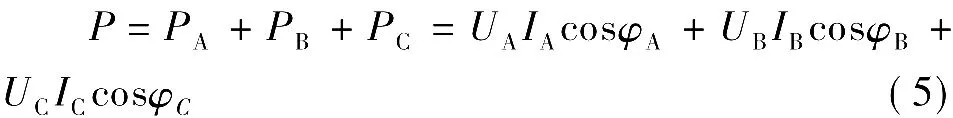
当负载为对称负载时，有

三相电路的总无功功率为

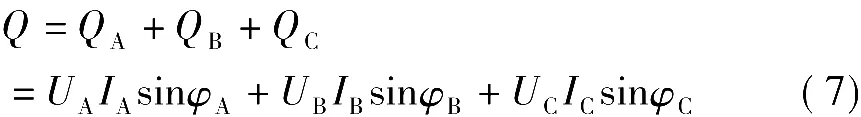
当负载为对称负载时，有

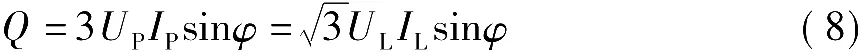
三相电路的总视在功率为

当负载为对称负载时，有

其中:

PA、PB和PC分别为各相负载的有功功率;

QA、QB和QC分别为各相负载的无功功率;

SA、SB和SC分别为各相负载的视在功率;

UA、UB和UC分别为三相相电压的有效值;

IA、IB和IC分别为三相相电流的有效值;

φA、φB和φC分别为三相负载的阻抗角;

UP和IP分别为相电压和相电流的有效值;

UL和IL分别为线电压和线电流的有效值;

φ为对称负载的阻抗角。

1.2 上述选择题的求解

由于所得的式(1)与式(9)不一致，故选择题中的A不正确。

由于式(2)所示

S2=与式(9)相同，故选择题中B正确。

由于式(3)与式(9)不一致，故选择题中C不正确。由于式(4)为S4=(PA+QA)+(PB+QB)+(PC+QC)=P+Q与式(9)不一致，故选择题中D不正确。

根据文献［1］，认为正确答案应为B。那么，答案A是否正确呢?实际上，答案A和答案B都是正确的。S1和S2是三相电路总视在功率的两种定义。就电力系统而言，S1更适合表示供电设备的容量或者损耗，如一些电工手册［2，3］就采用该公式;S2表示流量的概念。在系统潮流分析和稳定计算中所应用的绝大多数是复功率的概念，即使用S2，因而在多数《电工技术》和《电路》教材以及电工手册中都使用此公式。

那么，S1和S2之间存在什么关系呢?

2 S1和S2的关系

2.1 理论分析

根据式(1)可得

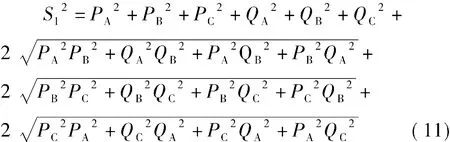
根据式(2)可得

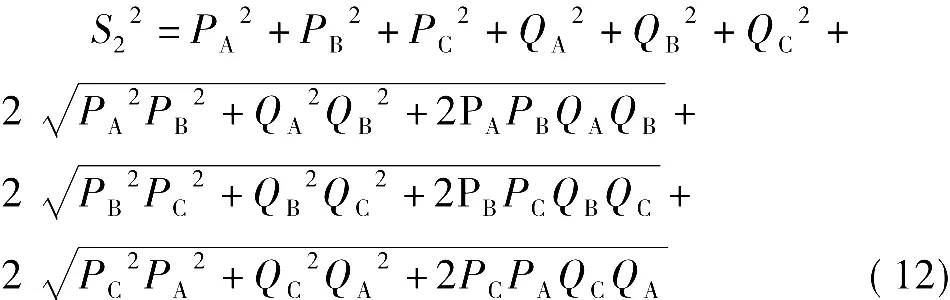
当负载为对称负载(ZA=ZB=ZC)时，PA=PB=PC，并且QA=QB=QC。比较式(11)和式(12)可得S12=S22，从而有 S1=S2。当负载为非对称负载时，要使S1=S2，必使

由上式可得到PA/QA=PB/QB=PC/QC，则有ctgφA=ctgφB=ctgφC，从而 φA=φB=φC。故当负载为满足φA=φB=φC的非对称负载时，S1=S2。

当负载为不满足φA=φB=φC的非对称负载时，比较式(11)和式(12)，因为有

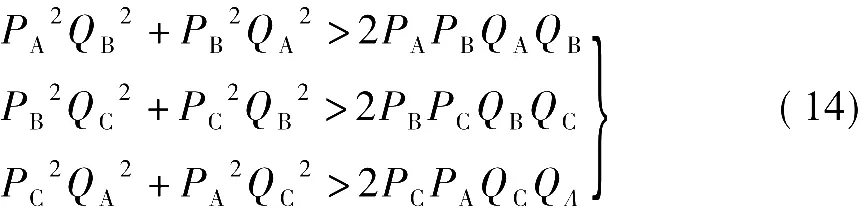
所以S12＞S22，从而有 S1＞S2。

2.2 计算示例

我们假设ZA=ZB=ZC=3+j4 Ω，则有

所以有S1=S2。

［示例2］满足φA=φB=φC的非对称负载计算

我们 假 设 ZA=10∠600Ω，ZB=15∠600Ω，ZC=30∠600Ω，则有

所以S1=S2。

［示例3］不满足φA=φB=φC的非对称负载计算

我们假设ZA=10∠00Ω，ZB=10∠300Ω，ZC=10∠600Ω，则有

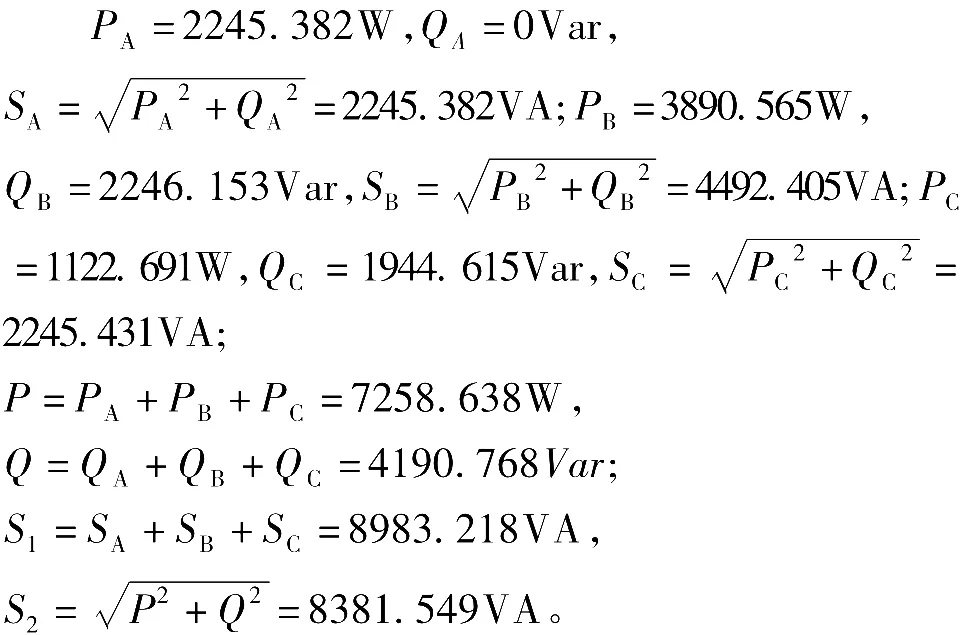
所以 S1＞S2。

2.3 不同示例负载时的功率图

图2(a)为对称负载时的功率图。图中的S1和S2为同一线段，即有S1=S2。

图2(b)为非对称负载满足φA=φB=φC时的功率图。图中的S1和S2为同一线段，即有S1=S2。

图2(c)为非对称负载不满足φA=φB=φC时的功率图。图中的S1为一折线，而S2为一线段显然S1＞S2。

3 结语

S1=SA+SB+SC和是两种计算三相电路总视在功率的公式。理论分析、计算示例和功率图都证实:当负载为对称负载时，S1=S2;当负载为满足φA=φB=φC的非对称负载时，S1=S2;当负载为不满足φA=φB=φC的非对称负载时，S1＞S2。

2 不同示例负载时的功率图

［1］ 周新云.电工技术［M］.北京:科学出版社，2005年2月.

［2］ 牛新国.电工技术常用公式与数据手册［M］.北京:金盾出版社，2001年8月.

［3］ 方大千等.简明电工速查运算手册［M］.北京:中国水利水电出版社，2004年9月.