土的应力应变关系中柔度矩阵的研究

卢 曦，施维成

(1.江苏技术师范学院 数理学院，江苏 常州213001;2.常州工学院土木建筑工程学院，江苏 常州213002)

在描述土的应力应变关系时，经常使用下式:{ dε}=[C]· { dσ}，式中:{dε}为应变增量;［C］为柔度矩阵;{dσ}为应力增量。

主应力空间中的柔度矩阵［C］第i行第j列的元素Cij表示当j方向施加单位应力增量，而其它方向应力增量为0时，在i方向所产生的应变增量［1］。主对角线元素Cii表示在i方向单向加荷时该方向上所产生的变形，非主对角线元素Cij(i≠j)表示在j方向单向加荷时i方向上所产生的变形。大量试验结果表明，在单向加荷的应力路径下，加荷向产生压缩变形［2］，且侧向变形量一般要小于加荷向变形量，所以土的柔度矩阵［C］要满足主对角线元素为正和主对角线元素占优势这2个条件［3-4］。殷宗泽等从塑性柔度矩阵主对角线元素与非主对角线元素之间的关系出发，证明了以经典塑性理论为基础的弹塑性模型的土体应力-应变柔度矩阵不能满足主对角线元素应占优的条件［5］。笔者将从代数学角度得出柔度矩阵同时满足主对角线元素为正和主对角线元素占优势这2个条件时，柔度矩阵行列式的特点。

1 土的柔度矩阵行列式特点

为简单起见，这里研究用主应力表示的柔度矩阵［C］，其可写成一个3×3的矩阵:

在描述土的应力应变关系时，［C］需要满足主对角线元素为正和主对角线元素占优势这两个条件，用数学表达式可以表示成:

下面探讨此时柔度矩阵［C］的行列式特点。

1.1 行列式非0

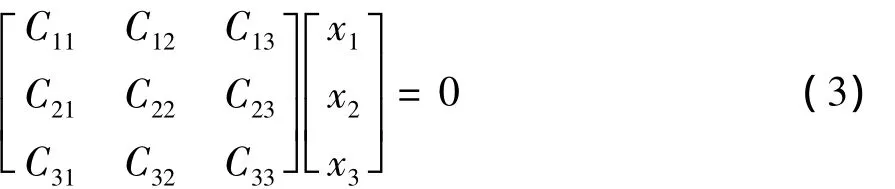
将式(3)展开并移项可得:

将式(4)等式两边取绝对值，并由绝对值三角不等式可得:

1.2 行列式大于0

根据行列式的定义，不妨按［C］的行列式第1行展开，可得:

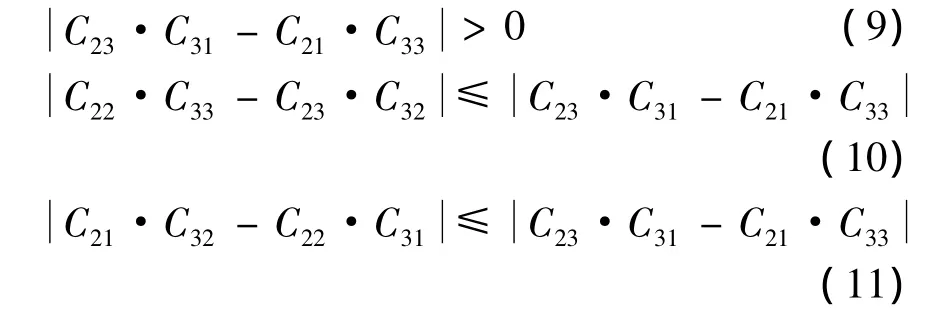
对不等式(10)、式(11)两端同时乘以 -1，可得:

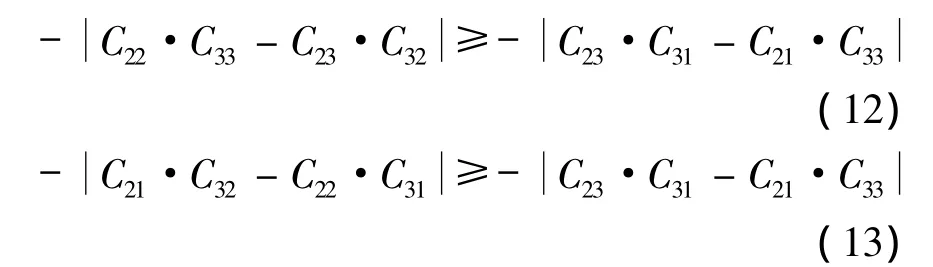
由式(2)可知，柔度矩阵主对角线元素占优时，有:

由绝对值三角不等式，并结合式(12)、式(13)可得:

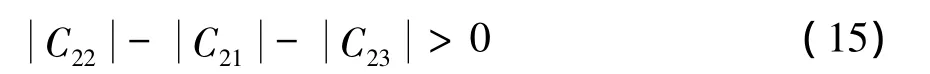
由式(9)、式(14)、式(15)可知:

而根据行列式的性质，有:

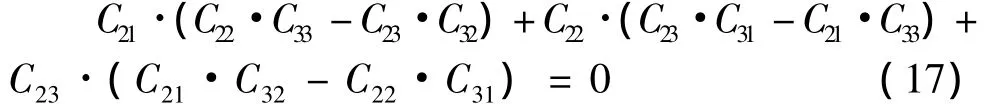
式(16)与式(17)矛盾，故不可能是3者中的最大值。

由式(2)可知，主对角线元素为正时，Cii＞0，即主对角线元素C11＞0，C22＞0，C33＞0。主对角线元素为正且主对角线元素占优时，有C22＞，因此:

由绝对值三角不等式，并结合式(12)、式(13)可得:

由式(2)可知，柔度矩阵主对角线元素占优时，有:

结合式(18)～式(20)，可得:

以上证明过程显示，［C］需要满足主对角线元素为正和主对角线元素占优势这两个条件，则其行列式必定大于0。

2 传统弹塑性模型的塑性柔度矩阵

由以上分析可见，式(21)可以作为评价土的本构模型合理性的一个方法。对于土的应力应变关系［6］，应用研究最为广泛、最被普遍认可的是弹塑性理论，在该理论框架内已经建立了包括剑桥模型［7］在内的很多模型。下面对传统弹塑性模型的塑性柔度矩阵［Cp］［8］进行分析:

［Cp］的行列式为:

将式(23)进行行列式展开，可得:

可见，传统弹塑性模型的塑性柔度矩阵行列式等于0，不能满足主对角线元素占优的条件，因此基于传统弹塑性理论建立的本构模型在描述土的力学性质时有其局限性。

3 结语

土体的力学性质决定了其柔度矩阵要满足主对角线元素为正和主对角线元素占优这2个条件。使用代数学方法研究了主应力表示的柔度矩阵，证明了这2个条件同时满足时，土的柔度矩阵行列式必大于0。因而，行列式是否大于0就可以作为判断土的本构模型合理性的一个方法。用这种方法对传统弹塑性模型的塑性柔度矩阵进行了研究，发现传统弹塑性模型的塑性柔度矩阵行列式等于0，不能满足主对角线元素占优的条件，在描述土的力学性质时有其局限性。

［1］张坤勇.考虑应力各向异性土体本构模型及其应用研究［D］.南京:河海大学，2004:54-55.

［2］施维成，朱俊高，何顺宾，等.粗粒土应力诱导各向异性真三轴试验研究［J］.岩土工程学报，2010，32(5):810-814.SHI Wei-cheng，ZHU Jun-gao，HE Shun-bin，et al.Stress induced anisotropy of coarse-grained soil by true tri-axial tests［J］.Chinese Journal of Geotechnical Engineering，2010，32(5):810-814.

［3］殷宗泽，徐志伟.土体的各向异性及近似模拟［J］.岩土工程学报，2002，24(5):547-551.YIN Zong-ze，XU Zhi-wei.Anisotropy of soils and its approximate simulation［J］.Chinese Journal of Geotechnical Engineering，2002，24(5):547-551.

［4］钱家欢，殷宗泽.土工原理与计算［M］.2版.北京:中国水利水电出版社，1996:73-74.

［5］殷宗泽，卢海华，朱俊高.土体的椭圆-抛物双屈服面模型及其柔度矩阵［J］.水利学报，1996(12):23-28.YIN Zong-ze，LU Hai-hua，ZHU Jun-gao.The elliptic-parabolic yield surfaces model and its softness matrix［J］.Shuili Xuebao，1996(12):23-28.

［6］沈珠江.土的弹塑性应力应变关系的合理形式［J］.岩土工程学报，1980，2(2):11-19.SHEN Zhu-jiang.The rational form of stress-strain relationship of soils based on elasto-plasticity theory［J］.Chinese Journal of Geotechnical Engineering，1980，2(2):11-19.

［7］徐舜华，徐光黎，程瑶.土的剑桥模型发展综述［J］.长江科学院院报，2007，24(3):27-32.XU Shun-hua，XU Guang-li，CHENG Yao.Review of Cam-Clay model for soils［J］.Journal of Yangtze River Scientific Research Institute，2007，24(3):27-32.

［8］殷宗泽，朱俊高，刘汉龙，等.土工原理［M］.北京:中国水利水电出版社，2007:247-249.