基于小波变换的目标检测关键算法研究
曹 量, 李太君
0 引言
小波变换是近年得到广泛应用的数学工具。与傅里叶变换、Gabor变换相比,小波变换是空间和频率的局域变换,因而能有效地从信号中提取信息。它通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,解决了傅里叶变换不能解决的许多困难问题,因而被誉为“数学显微镜”[1]。基于小波变换具有低熵、去相关、“变焦”和选基灵活等特性并且在图像去噪和边缘检测中有突出的贡献,对目标检测中的这2个重要基础做了深入的研究,提出了改进的小波局部自适应算法,给出了高斯小波模极大值边缘检测方法。
1 小波分析的原理
设函数ψ(x)满足,用尺度因子S对ψ(x)进行放缩得到一组函数ψS(x)=ψ(x/S)/S,则在位置x处,函数f(x)的尺度为S的小波变换定义为:

其中ψ(x)称为小波函数,式(1)称为连续小波变换式。
如尺度S以二进方式离散取值,S=2i(i为整数),则可得到相应的二进小波变换

1.1 小波去噪原理
[2-3]。设一个被噪声污染的信号的基本模型为:

式中s(t)是信号,n(t)是一个服从的宽平稳高斯白噪声。令WTn(a,b)是n(t)的小波变换,a是尺度因子,b是平移因子,则有:

而:
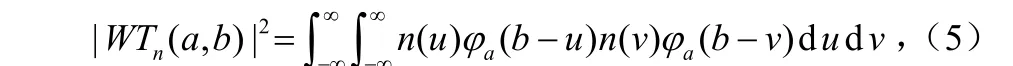
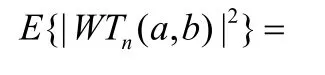
可看出,噪声小波系数的平均功率与尺度a成反比。可证明,对于所有尺度,噪声n(t)的小波变换离散细节信号系数的方差随着尺度的增加也会有规律地减小,即其中Da,Da-1为方差。而信号s(t)小波变换的值在跳变处随着尺度a的增加均表现出明显的峰值,其符号正负则决定于此阶跃是正跳变还是负跳变。
因为正交小波变换是线性变换,所以对观测g作离散小波变换,得到的小波系数y=Wg(W为二维正交小波换算子)仍由两部分组成,一部分是信号f对应的小波系数x=Wf,另一部分是噪声n对应的小波系数v=Wn,即y=x+v。Donoho[4]提出的小波阈值去噪方法在最小均方误差意义上是有效的并且可达到较好的视觉效果,它主要的理论依据为属于Besov空间的信号在小波域内其能量主要集中与有限的几个系数中,而噪声的能量却分布于整个小波域内,经小波分解后信号的系数要大于噪声的系数,因此采用阈值的办法可把信号系数保留,而使大部分噪声系数减少至0。
1.2 小波模极大值边缘检测原理
参考文献[1,5]。定义θ(x,y)为二维平滑函数,它在整个平面上的积分为1并且它在x和y为无限远处收敛到0。定义两个小波函数ψx(x,y)和ψy(x,y)为:

这样,图像f(x,y)的小波变换的两个分量在尺度为S时定义为:
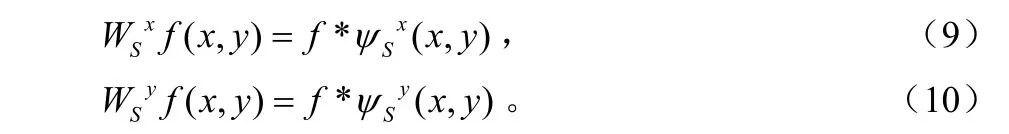
对于二进小波变换,就有:

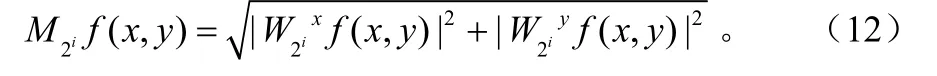
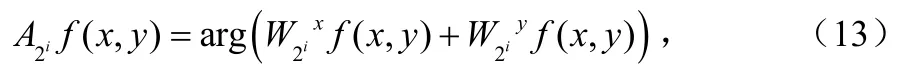
2 局部自适应阈值去噪算法
小波变换系数间存在一定的相关性[6]:①在相同的尺度下,重要的小波系数“聚集”在某些区域,如图像的边缘一般是重要的小波系数出现的区域,这种相关性称为尺度内的相关;②在不同的尺度(分辨率)下,图像特征对应着许多大数值的小波系数,这些系数之间应存在相关性,称其为尺度间的相关。这种相关性是小波变换分解过程中内在因有的,反映多尺度性。
这里依据尺度内的相关性提出一种改进的局部自适应阈值去噪算法。因为噪声图像小波系数的方差域局部平滑并且变换缓慢,所以高频子带中的每个小波系数X(i,j)的方差与邻域(一般先择方形领域)内的小波系数的方差具有高度相关性[2]。这样,可以选择(i,j)处小波系数的M×M邻域来估计X(i,j)的方差,估计的计算式可写为:
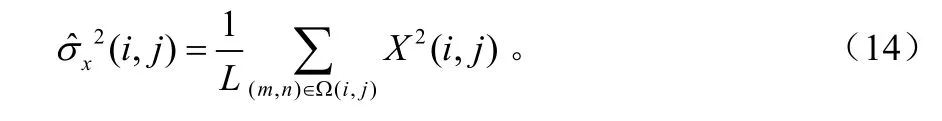

半软阈值法通过双阈值克服了硬阈值的过“扼杀”高频系数,使重构信号产生较小的均方差。半软阈值法[7]的阈值函数为:

比例萎缩法[8]根据最小均方差准则(MMSE),可以得出从X(i,j)中恢复S(i,j)的理想函数式
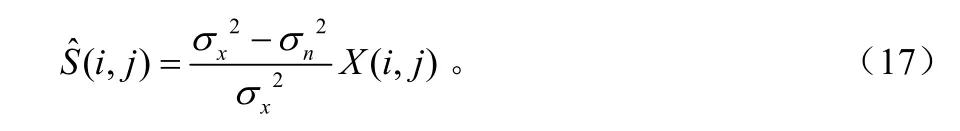
结合半软阈值法和比例萎缩法提出改进后的局部自适应的阈值函数:
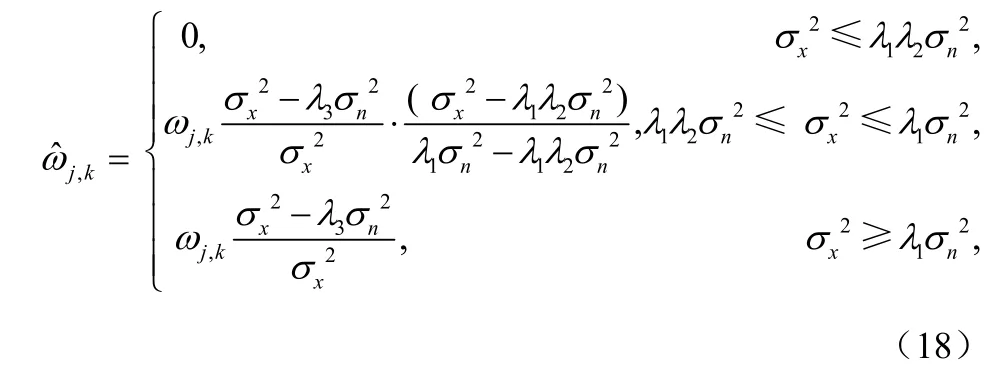
3 高斯小波模极大值边缘检测算法
Mallat[9]指出,使用平滑函数的一阶导数的极值进行检测优于使用二阶导数的零交叉检测。由于高斯函数的一阶导数具有很好的边缘检测的能力,现选择二维高斯函数的一阶导数作为小波函数。二维高斯函数的表达式为:,θ是一维高斯函数。θ(x,y)分别对x,y方向求偏导,并取相反数,得到:
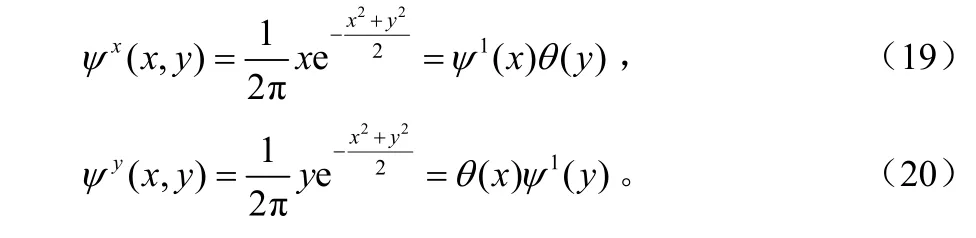
ψ1是对应于高斯函数一阶导数的一维小波。容易证明满足小波函数的容许条件,是一个二维小波。
高斯小波模极大值边缘检测的步骤为[7]:
①选定二维高斯平滑函数θ(x,y)为尺度函数,由式(19)、式(20)求出θ(x,y)在尺度S上的一阶编导数和作为小波函数;
②用式(9)、式(10)对图像进行小波变换,求得小波变换在S尺度上的两个分量
④根据直方图统计特性选定自适应阈值:将求得的模极大值边缘图像进行归一化,将图像划分成1 024个灰度级进行直方图统计,对灰度级从1/1024开始进行循环对边缘点个数进行累加,当累加得到的边缘点个数最终小于边缘点总数的k(0<k<1)倍时,则将该处的灰度值作为自适应阈值;
⑤用双阈值对边缘图像进行非极大值抑制,高阈值为第四步产生的自适应阈值,低阈值一般为高阈值的0.5倍,高于高阈值一定是边缘,低于低阈值一定不是边缘,高低阈值之间判断8领域是否都高于高阈值否则不是边缘点;
⑥对边缘图像进行边缘连接和边缘细化处理,输出边缘图像。
4 实验结果及分析
参考文献[10]。以大小为256×256,灰度级为256的lena图像为例,在Matlab中进行仿真。
这里边缘检测前的去噪算法选用db8小波基对图像进行5级分解。db8小波基支集长度长,消失矩和正则性高。消失矩阶数大,小波能量集中,正则性好,则二维图像重构后就越平滑。对于多层分解的小波系数,层数越大,噪声能量会变得越小。由于阈值的自适应性,每一层的噪声和图像有用信息都会被最大程度的进行分解。当λ1=1.9,λ3=0.6图像去噪效果较好,加噪方差为0.01时的实验结果如图2所示。

图1 图像去噪结果比较
采用峰值信噪比(PSNR)和均方误差(MSE)在加噪方差分别为0.005、0.01、0.02时对去噪算法的效果进行定量分析比较,实验结果如表1所示。
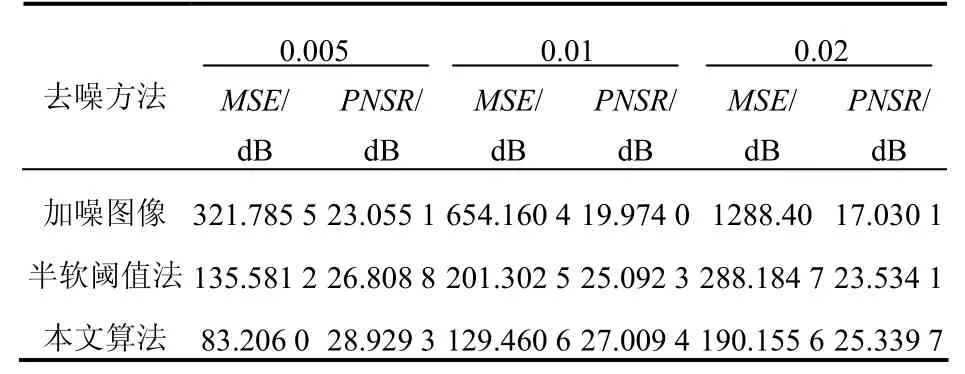
表1 图像去噪峰值信噪比和均方误差的比较(单位:dB)
当尺度S=21时这里算法的实验结果如图 2(d)所示。根据图2所示比较结果,这里的边缘检测算法明显优于传统的Roberts算子、Sobel算子等,与经典的Canny算子的检测结果相比,在眼睛、帽子和头发上的细节信息多一些,其装饰更为真实。但在少部分弱边缘存在断线的情况,笔者分析这里主要的原因是阈值处理不当引起的过“扼杀”所致。

图2 图像边缘检测结果比较
5 结语
在分析噪声的小波特性和小波去噪原理的基础上,根据小波变换系数尺度内的相关性提出了一种新的局部阈值策略,还结合半软阈值法和比例萎缩法提出了一种改进的小波局部自适应阈值图像去噪算法;在分析了小波模极大值边缘检测原理的基础上,给出了二维高斯函数模极大值边缘检测的方法,提出了用直方图的统计特性进行自适应阈值的选取,并通过双阈值策略进行非极大值抑制。实验结果也表明了这里算法相对于传统算法的优越性,为图像分析等后期的目标检测工作打下了坚实的基础。
参考文献
[1]章毓晋.图象分割[M].北京:科学出版社,2001.
[2]赵继印.小波自适应比例改进算法在图像去噪中的应用[J].光电工程,2006,33(01)81-84.
[3]金彩虹. 基于图像边缘信息的多小波阈值去噪方法[J].通信技术,2008,41(12):247-249.
[4]DONOHO D L,JOHNSTONE I M.Adapting to Unknown Smoothness via Wavelet Shrinkage[J].Journal of the American Statistical Association,1995, 90(12):1200-1224.
[5]王青竹.多层次自适应空间系数高斯小波图像边缘检测[J].中国图像图形学报,2009,14(07):1348-1353.
[6]董立文.一种基于小波变换的图像去噪方法[J].鞍山科技大学学报,2004,27(03):212-215.
[7]赵继印.基于半软阈值法的图像小波去噪方法[J].大庆石油学院学报,2004,28(01):63-66.
[8]MIHCAK M K,KOZINTSEV I,RAMCHANDRANK.Low-complexity Image Denoising based on Statistical Modeling of Wavelet Coefficient[J].IEEE Trans On Signal Processing, 1999,6(12):300-303.
[9]MALLTA S G,ZHONG S.Characterization of Signals from Multiscale Edges[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(07):710-732.
[10]何劲.基于Curvelet变换与小波包变换联合的图像去噪算法[J].通信技术,2008,41(01):140-142.

