太阳能烟囱自然通风的一维稳态模型

苏亚欣，柳仲宝

(东华大学 环境科学与工程学院，上海201620)

自然通风是一种热压或风压来驱使空气流动而进行的通风换气方式。与机械通风相比，自然通风不消耗常规能源，具有节能的特点。合理的自然通风设计能够改善室内空气品质，提高室内环境的舒适性等优点[1－2]。然而自然通风的驱动力，即热压与风压，与机械驱动力相比却较为微弱，因而在一定情况下自然通风的使用受到了限制。太阳能烟囱是一种利用热压强化自然通风的有效方法。

太阳能烟囱将自然通风和太阳能相结合，在太阳能烟囱的上部安装有太阳能集热器，用于吸收太阳能，加热烟囱内的空气产生因浮升力而导致的抽吸作用，使冷空气从建筑物的下部进入，热空气从烟囱上部排出，在建筑物内形成空气流动，达到室内通风降温的目的。很多作者对不同形式的太阳能烟囱的自然通风热特性进行了实验测试[3－7]，发现太阳能烟囱的综合性能与当地日照条件、太阳射线入射角以及太阳能烟囱的结构参数等因素有关。模型研究也吸引了不少研究人员的注意。Ong等[8]基于一维稳态传热模型，在忽略玻璃盖板和集热墙的导热热阻的基础上，建立了一个由玻璃盖板、集热墙和烟囱内的空气的热平衡方程，计算了烟囱内的空气流量、集热效率以及玻璃盖板和墙体平均温度等参数。Bansal等[9]应用该模型，在对玻璃表面与室外空气的对流换热系数以及空气质量流量表达式中一个比例系数进行修正之后，计算了太阳能烟囱的空气流量随太阳辐射强度的变化。Mart1′－Herrero等[10]在Ong等[8]模型的基础上进一步提出了一个非稳态模型。Bassiouny等[11]应用 Ong等的模型[8]和CFD模拟对比研究了相同的太阳能烟囱的自然通风特性。

上述模型忽略了玻璃盖板和集热墙的内部导热热阻。然而，由于集热墙材料的导热系数通常比较小，在一个表面受到较强的太阳辐射而另一个表面暴露于空气中时，必然会引起墙体内部的温度梯度。在忽略了此温度梯度的前提下的数学模型将使会产生一定的误差。本文考虑了玻璃盖板和集热墙的内部导热热阻，在分析太阳能烟囱的各个换热过程的能量平衡的基础上，建立一个修正的太阳能烟囱自然通风的数学模型。

1 太阳能烟囱的物理和数学模型

1.1 物理模型

太阳能烟囱物理模型如图1所示，主要由玻璃盖板、集热墙以及空气通道所构成。烟囱的高度为2m，宽度为0.45m，空气通道夹层厚度在0.1～0.3m之间变化，下部空气入口的高度为0.1m。烟囱的外层为厚度为4mm的玻璃盖板，太阳辐射照射到玻璃盖板后，一部分被玻璃吸收，其余部分穿透玻璃，到达集热墙。集热墙表面附加一层对太阳辐射吸收率较高的选择性涂层，集热墙吸收入射太阳辐射后温度升高，从而加热夹层内的空气，使空气形成向上运动的自然对流，从烟囱顶端流出至室外。室内空气则通过集热墙下部的入口流入空气通道，从而使室内的空气形成自然通风。

1.2 数学模型

整个太阳能烟囱的能量平衡关系包括集热墙和玻璃盖板对太阳辐射的吸收及其内部的导热过程、空气在太阳能烟囱内被集热墙和玻璃盖板加热的自然对流换热过程。集热墙和玻璃盖板厚度与其高度和宽度相比较薄，可视为大平板一维稳态导热，集热墙和玻璃盖板的热物性参数为常数。夹层内的空气对太阳辐射不吸收，室内空气温度与室外环境空气温度保持恒定，空气的物性参数假设是温度的函数。此外，天空视为具有当量温度的黑体，平均入射太阳辐射强度H(W／m2)为常量。图2为太阳能烟囱的传热过程的示意图。

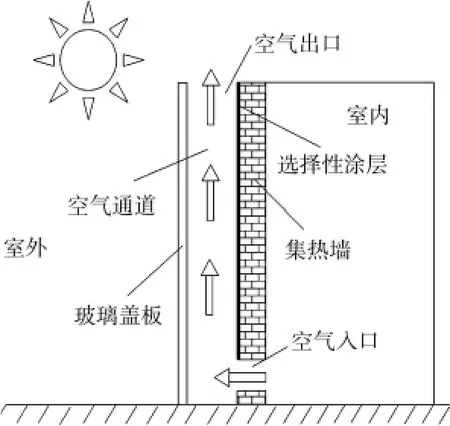
图1 太阳能烟囱的物理模型

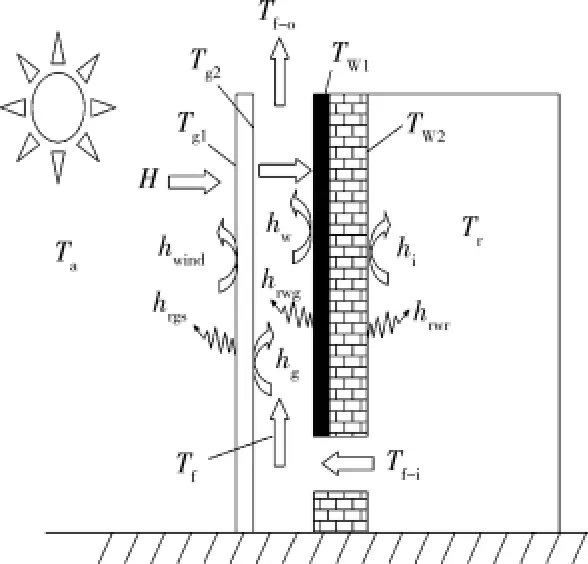
图2 太阳能烟囱的传热过程

1.2.1 玻璃盖板内、外表面的能量平衡方程 玻璃盖板外表面接受来自太阳的辐射能以及与室外环境空气进行对流换热，并以导热的形式把热量传递到玻璃盖板内表面。玻璃盖板内表面与夹层内的空气进行对流换热，同时与集热墙外表面进行辐射换热。分析其换热过程的能量平衡，可得玻璃盖板内、外表面的能量平衡方程分别为：

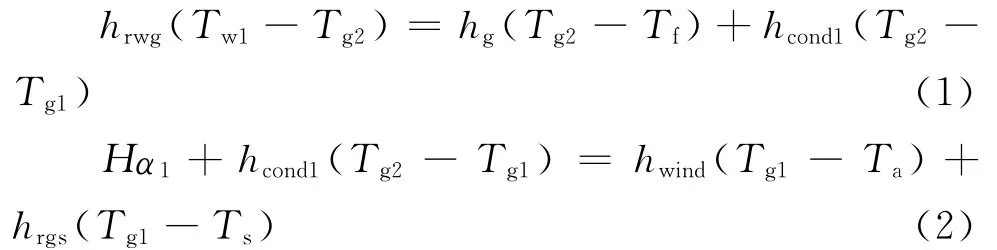
式中各参数计算如下：

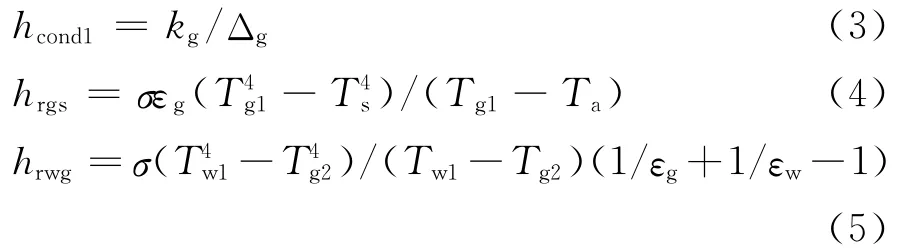
天空温度采用下面的公式计算[12]：

室外空气与玻璃外表面的自然对流换热系数为[13]：

通道空气与玻璃的自然对流换热系数hg＝Nu采用下面的经验公式计算[14]：

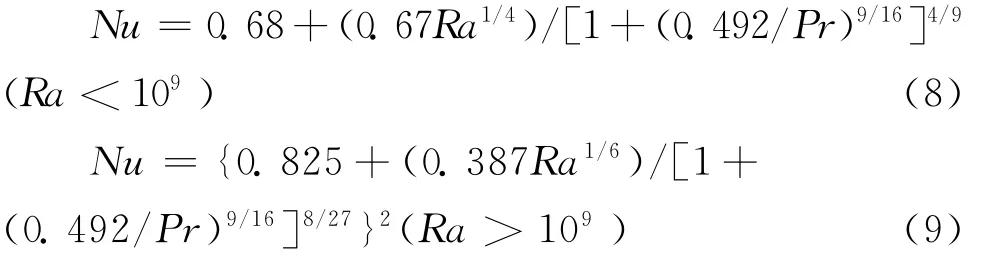
1.2.2 通道夹层内空气的能量平衡方程 通道夹层内的空气与玻璃盖板内表面以及集热墙外表面通过对流换热而被加热，能量平衡可表示为：

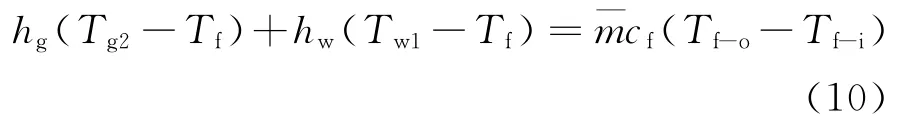
式中集热墙外表面的自然对流换热系数hw＝，Nu按式(8)、(9)计算。

实验研究[15]表明烟囱的进、出口空气温度与烟囱通道夹层内平均空气温度有如下关系：

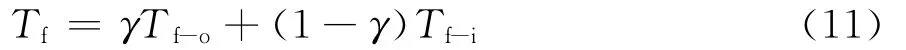
式(11)代入式(10)，得：

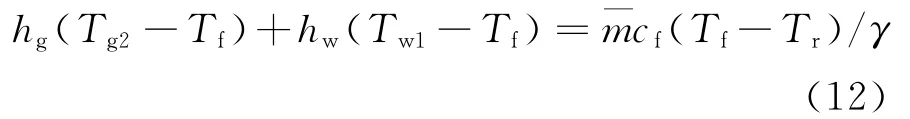
式中平均温度计算因子γ＝0.74[15]。

烟囱通道内的空气质量流量¯m由下式计算[16]：

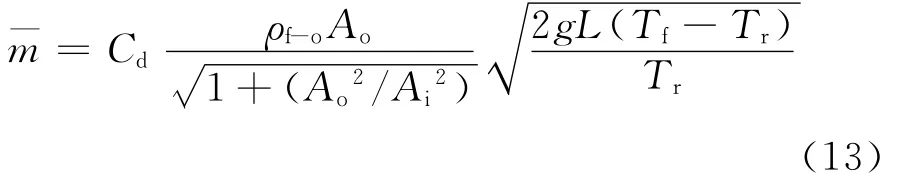
式中流量系数Cd＝0.57[17]。

1.2.3 集热墙内、外表面的能量平衡方程 集热墙外表面的换热过程包括它对太阳辐射的吸收、与通道内空气的对流换热、与玻璃盖板内表面的辐射换热以及集热墙内的一维稳态导热，集热墙内表面的换热过程包括它与室内空气的对流换热、与室内空间的辐射换热以及集热墙内的一维稳态导热。分析其换热过程的能量平衡，可得集热墙内、外表面的能量平衡方程分别为：

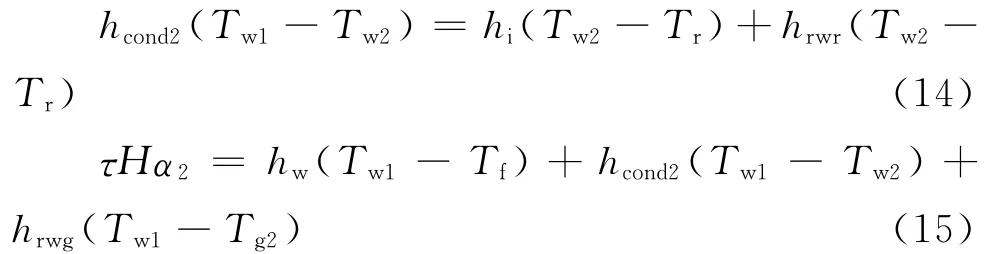
式中：

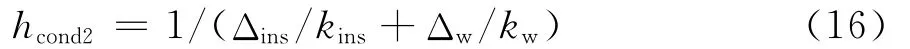
集热墙对室内空气的辐射换热系数为：

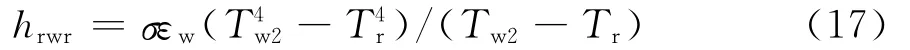
1.2.4 空气的物性参数 在太阳能烟囱数学模型中，空气通道内空气温度的变化范围在300～350K之间，所以通道内的空气物性参数可以假定为空气温度的线性函数，计算如下[14]：

2 结果与分析

应用上述模型，对图1所示的太阳能烟囱的自然通风进行了模型计算，并与文献[8]的简化模型结果及实验测试结果进行对比。

2.1 模型结果可靠性验证

文献[8]对图1所示的太阳能烟囱自然通风时玻璃盖板、集热墙以及烟囱内的空气平均温度进行了实验测试。实验过程中为了保证集热墙的热吸收效率，在集热墙的室内侧增加50mm厚的绝热材料以减少集热壁面热损失。使用铜－康铜热电偶(＋0.5℃)测量集热墙、空气以及玻璃盖板的温度，在集热墙表面布置了5个测点，空气通道高度上布置了7个测点，而玻璃盖板表面只布置了1个测点。烟囱进出口处的空气流速使用热线风速仪(＋0.03 m／s)进行测量。本文用上述修正模型对文献[8]的测试工况进行了计算，并将模型结果与其测试结果以及文献[8]的简化模型结果进行了对比，如图3－图12所示。从结果对比来看，本文的修正模型的计算结果与实验测试结果的趋势一致。当空气通道的厚度为0.1m时，文献[8]对通道内的空气平均温度的模型计算结果比实验结果低1.6℃(相对误差为4.72%)，本文的修正模型结果比实验结果低0.8℃(相对误差为2.36%)，如图3所示；文献[8]对集热墙平均温度的模型结果与实验结果的误差为4.5℃，而本文的结果与实验结果的误差为3.1℃，如图4所示。本文的修正模型同样提高了对通道内空气质量流量的计算结果，如图5所示，空气通道厚度在0.1～0.3m范围内时，模型结果与实验结果的相对误差为10.96%～17.65%，比原模型的相对误差(23.65%～30.66%)有一定的提高。

与文献[8]的简化模型相比，本文的模型结果整体上更加接近对应的实验数据，表明本文的修正模型具有可靠性并在一定程度上提高了模型的预测准确度。

2.2 太阳能烟囱结构参数对自然通风特性的影响

太阳能烟囱主要的结构参数是其空气通道的厚度，其大小影响通道内的空气在受热后的自然对流流动与换热过程，从而影响自然通风的效率。利用上述数学模型，对图1所示的太阳能烟囱进行了结构参数的计算，图3和图4为太阳能烟囱内的空气平均温度、集热墙平均温度随烟囱内空气通道厚度变化的计算结果，其中实验数据取自文献[8]。

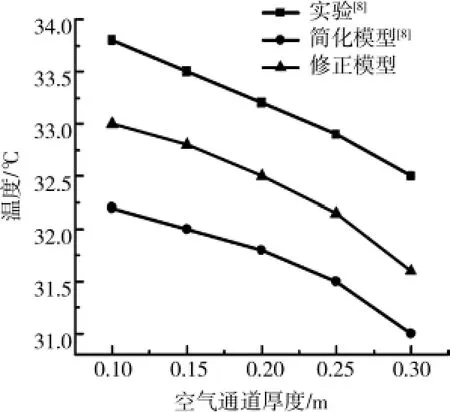
图3 空气温度随空气通道厚度的变化(太阳辐射强度H＝200W／m2，Ai＝0.045m2)

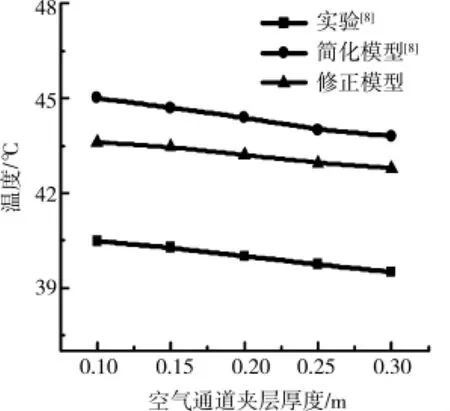
图4 集热墙温度随空气通道厚度的变化(太阳辐射强度H＝200W／m2，Ai＝0.045m2)

由图3和图4的结果看到，玻璃盖板的温度、空气的温度以及集热墙的温度均随着通道厚度的增加而降低，而通风量则随着空气通道厚度的增加而增大，如图5所示。这表明随着空气通道厚度的增加，太阳能烟囱的自然通风能力得到一定的增强。当空气通道的厚度超过一定值后，通风量则不再增加。

太阳能烟囱通道内空气的自然对流过程受太阳能加热作用而加强，同时通道壁面对空气的阻力随着气流速度和空气黏度的增大而增大。在相同辐射强度下，空气吸收太阳能而升温，其黏度随之增加。当空气通道厚度较小时，空气黏度增加的程度较高，从而使通道壁面对空气的阻力也增加。随着空气通道厚度的增加，通道内的空气质量增多，使得空气的温升减缓，从而降低了空气黏度，使空气阻力下降，从而使空气的速度增大，因此增大了通道内的空气质量流量，同时使得玻璃和集热墙表面的对流换热系数增加，使得玻璃和集热墙的温度降低。当空气通道的厚度超过一定值后，由于截面积的增大对速度的影响超过了太阳辐射的加热对空气所受浮力的影响后，则空气的流速将难以继续增加，从而使得通道内的空气质量流量不再增加。因此合理的太阳能烟囱设计存在一个最佳的空气通道厚度。

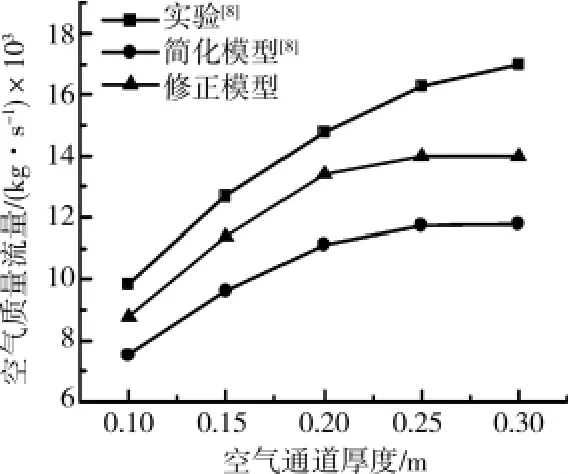
图5 空气质量流量随空气通道厚度的变化(太阳辐射强度H＝200W／m2，Ai＝0.045m2)

2.3 太阳辐射强度对自然通风特性的影响

太阳辐射强度影响通道内空气的温升，从而影响了自然通风的热压。图6－图8给出通道空气的温度、集热墙的温度以及通风量均随太阳辐射强度的变化结果。随着太阳辐射强度的增大，集热墙温度升高，通过自然对流换热过程使通道内的空气被加热而升温，空气所受浮升力的增强使得空气向上运动的速度增大，从而使通道内的空气流量增加，自然通风作用得到了加强。当H＝200W／m2时通道内的空气温度为33℃，当H＝600W／m2时通道内的空气温度升高为38.2℃。

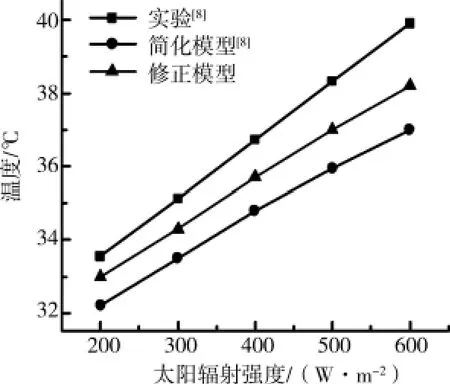
图6 空气温度随太阳辐射强度的变化规律(空气通道厚度d＝0.1m，Ai＝0.045m2)

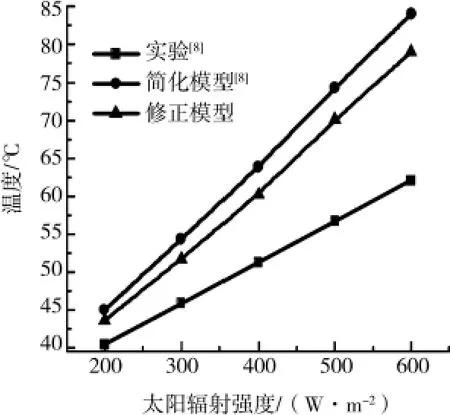
图7 吸热墙温度随太阳辐射强度的变化规律(空气通道厚度d＝0.1m，Ai＝0.045m2)

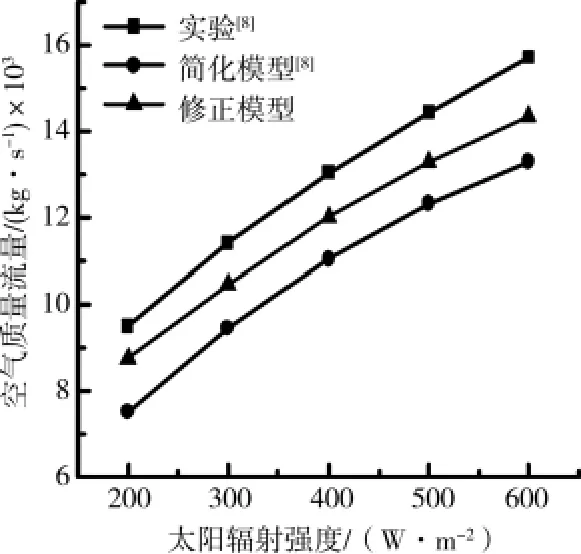
图8 空气质量流量随太阳辐射强度的变化规律(空气通道厚度d＝0.1m，Ai＝0.045m2)

2.4 集热效率的变化

太阳能烟囱的集热效率计算如下[8]：

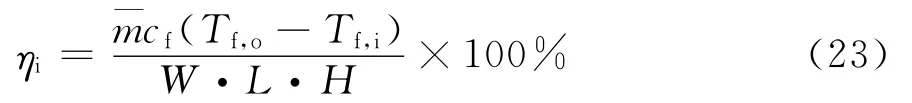
它表示太阳能烟囱所吸收的太阳辐射与入射到太阳能烟囱的总太阳辐射的比。

图9和图10分别示出了太阳能烟囱的集热效率随空气通道厚度以及太阳辐射强度的变化结果。当空气通道的厚度在0.1～0.3m范围内变化时，本文的模型结果与实验数据的相对误差为14.9%～18.1%，与原模型的相对误差(22.91%～26.76%)相比，修正模型的结果有一定的改善，如图9所示。模型结果同时表明，随着通道厚度的增加，集热效率增大。随着太阳辐射强度的增大，集热效率增大。通道厚度和太阳辐射强度增加后，使烟囱内的自然对流过程得到一定的强化，因而增强了通道内的自然对流(通风)过程。

2.5 对修正模型的进一步讨论

在本文修正模型中，烟囱通道内的空气温度采用了一个平均值，并用于计算玻璃盖板和集热墙的能量平衡。此外，烟囱通道内玻璃盖板和集热墙表面的对流换热系数也采用的平均值。然而在空气流经集热墙表面被加热的过程中，空气的温度将逐渐升高，同时在集热墙和玻璃内表面上形成的空气边界层的变化也将影响局部的对流换热系数的变化。在计算空气、玻璃以及集热墙的能量平衡的时候，采用一个合理分布的局部空气温度以及局部换热系数将有助于进一步提高模型的计算结果。

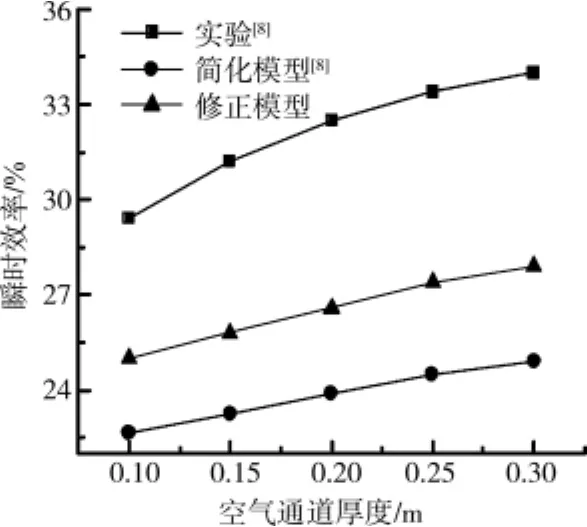
图9 集热效率随空气通道厚度的变化规律(太阳辐射强度H＝200W／m2，Ai＝0.045m2)

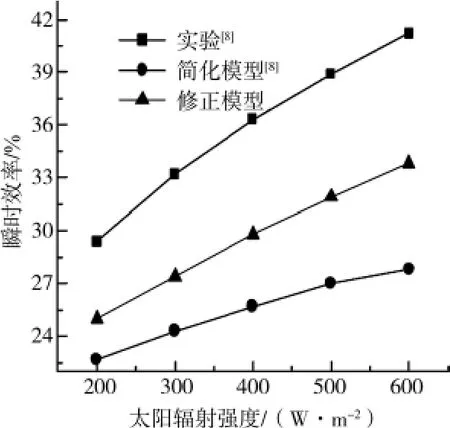
图10 集热效率随太阳辐射强度的变化规律(空气通道厚度d＝0.1m，Ai＝0.045m2)

3 结 论

在文献研究的基础上，考虑了盖板玻璃和集热墙的导热热阻的影响，应用一维稳态传热模型对太阳能烟囱自然通风的数学模型进行了修正。修正模型的计算结果与文献相关实验测试结果的对比表明本文的修正模型具有可靠性。同时与文献的简化模型的比较表明，本文的修正模型提高了计算结果的准确性。模型计算结果表明太阳能烟囱的自然通风量随着空气通道厚度的增加而增大，达到一定值后保持不便。因而太阳能烟囱设计存在一个最佳的空气通道厚度。

[1]FORDHAM M.Natural ventilation[J].RenewableEnergy，2000，9：17－37.

[2]万鑫，苏亚欣.现代建筑中自然通风技术的应用[J].建筑节能，2007，35(9)：9－12.WAN XIN，SU YA－XIN.Application of natural ventilation to modern architecture design [J].Construction Conserves Energy，2007，35(9)：9－12.

[3]AFRIYIE J K，NAZHA M A A，RAJAKARUNA H，et al.Experimental investigations of a chimneydependent solar crop dryer[J].Renewable Energy，2009，34：217－222.

[4]CHEN Z D，BANDOPADHAYAY P，HALLDORSSON J，et al.An experimental investigation of a solar chimney model with uniform wall heat flux[J].Building and Environment，2003，38：893－906.

[5]李安桂，郝彩侠，张海平.太阳能烟囱强化自然通风实验研究[J].太阳能学报，2009，30(4)：460－464.LI AN－GUI， HAO CAI－XIA，ZHANG HAI－PING.Experimental study on solar chimney for natural ventilation[J].Acta Energiae Solaris Sinica，2009，30(4)：460－464.

[6]ARCE J，JIMENEZ M J，GUZMAN J D，et al.Experimental study for natural ventilation on a solar chimney[J].Renewable Energy，2009，34：2928－2934.

[7]MATHUR J，MATHUR S，ANUPMA.Summer performance of inclined roof solar chimney for natural ventilation[J].Energy and Buildings，2006，38：1156－1163.

[8]ONG K S，CHOW C C.Performance of a solar chimney[J].Solar Energy，2003，74：1－17.

[9]BANSAL N K，MATHUR J，MATHUR S，et al.Modeling of window－sized solar chimneys for ventilation[J].Building and Environment，2005，40：1302－1308.

[10]MART1′－HERRERO J，HERAS－CELEMIN M R.Dynamic physical model for a solar chimney[J].Solar Energy，2007，81：614－622.

[11]RAMADAN BASSIOUNY，NADER S A，KOURA.An analytical and numerical study of solar chimney use for room natural ventilation[J].Energy and Buildings，2008，40：865－873.

[12]DUFFIE J A，BECKMAN W A.Solar Energy Thermal Process[M].New York：John Wiley ＆Sons Inc.，1974.

[13]MCADAMS W H.Heat Transmission[M].3rd ed.New York：McGraw－Hill，1994.

[14]INCROPERA F P，DEWITT D P.Fundamentals of Heat and Mass[M].4th ed.New York：John Wiley ＆Sons Inc.，1996.

[15]HIRUNLABH J，KONGDUANG W，NAMPRAKAI P，et al.Study of natural ventilation of houses by a metallic solar wall under tropical climate[J].Renewable Energy，1999，18(1)：9－19.

[16]BANSAL N K，MATHUR R，BHANDARI M S.Solar chimney for enhanced stack ventilation[J].Building and Environment，1993，28：373－377.

[17]FLOURENTZOU F，ROULET C A.Natural ventilation for passive cooling：measurement of discharge coefficients[J].Energy and Buildings，1998，27：283－292.