在数学教学中培养学生数学逻辑思维习惯

严亚娣

（中山市中等专业学校 广东 中山528400）

在数学教学中培养学生数学逻辑思维习惯

严亚娣

（中山市中等专业学校 广东 中山528400）

首先阐述了在职业中专培养学生数学逻辑思维能力的必要性，分析了数学知识讲授与培养学生数学逻辑思维的关系。然后着重剖析了构建数学知识网络对培养学生数学逻辑思维能力的作用以及激发学生的数学研究精神对培养学生数学逻辑思维习惯的意义。最后还讨论了培养学生数学逻辑思维能力的教学心理和激励机制。

数学；逻辑思维；能力；习惯；开拓创新

问题的缘起

学数学，部分中专学生容易陷入“现买现卖”的功利误区，即希望学到或记住几条数学公式，以便日后用来“代入”计算。这种学数学观念的结果往往是对数学知识囫囵吞枣，浮光掠影，不求甚解，记不住，不会用，考试时勉强通过，考试后前功尽弃。这是任何一位数学教师都不愿见到的结果。

我们不要求学生都能成为某行业专家，但我们却有责任让每个中专生通过短短的几年学习逐步成为创新的好手。创新，绝非标新立异，异想天开，更不能违反规律，主观蛮行；创新，应是在严密的逻辑思维基础上的开拓，在严密的科学精神指导下的变革。我们要培养创新型人才，首先就得培养学生的科学精神，培养他们的逻辑思维能力，培养他们学会分析事物，找到事物发展的客观规律，再按规律进行开拓创新。创新是现代人一种不可或缺的素质。因此，学数学，绝不仅是学几条数学公式、定理，以方便计算，更重要的是要通过对数学知识循序渐进的学习，逐步学会数学逻辑思维方法，形成逻辑思维习惯，并把这种思维方法用于日后的数学学习中，进而推广到其他领域，作为创新的基础。这种意义是远远超越于数学学习本身的。

数学知识是培养数学逻辑思维的载体

笔者认为，学习文化科学知识的目的不外是：扩大视野，开拓智力。无视野之扩大无以开拓智力，不开拓智力无以进一步扩大视野，前为载体，后为目的，相辅相成，不可分割，互为辩证统一体。因此，数学知识是培养数学逻辑思维的载体。也就是说，数学逻辑思维的培养必须通过学习数学知识，而学习数学知识的根本目的在于培养数学逻辑思维能力与习惯并反过来促进进一步学习数学知识。

知识与思维能力不能通过DNA得以遗传。数学逻辑思维方法需要在循序渐进地学习数学的过程中不断总结，才能逐步领悟、掌握和形成习惯。而数学逻辑思维模式形成后则不仅能促进对数学知识学习的深入，更可以开拓和发展新的数学知识。数学史上这种先例是不可胜数的。其中一个突出的例子是笛卡儿创立直角坐标系，把变量与变量的关系几何化。后来的数学家们沿着笛卡儿这种逻辑思维的路子，把变量的关系研究得越来越深入细致，并开拓出了函数、解析几何、微积分等数学分支，继而又把这种逻辑思维方法推广到诸如化学、物理、天文、地理、生物乃至经济、社会各个领域，引来了人类文明的一次巨大飞跃。

学生必须在数学知识的学习中学会数学逻辑思维方法，逐步形成数学逻辑思维习惯，这样才有可能成为创新型人才，这已是毋庸置疑的结论。为此，数学教师在教学中，除了要把数学知识传授给学生外，还要对学生揭示在这些数学知识中隐含着的数学家们的逻辑思维方法，让学生领悟、掌握、形成习惯、会运用。在讲授数学概念、定理、公式时要这样做，在解例题、习题时，更要引导学生通过分析，运用逻辑思维方法，找到问题解决的切入口，最后得到合乎逻辑的解法，并鼓励学生在逻辑思维的基础上，另辟蹊径，创新解法。

如高中三角中角度单位弧度制的引进，一般只重视单位的定义、弧度制与度分秒单位制的换算等。教师不妨提出这样的问题：为什么角度单位要用弧度制？其实，弧度制把角度变成了实数，那么，三角函数与角度之间的关系就变成了两个实数集合的映射关系了。这才是采用弧度制的根本理由。

又如一道简单的不等式题：

可见，小问题也可以寓于数学逻辑思维方法的应用中，这是我们在教学上不可忽视的。

构建数学知识网络是培养学生数学逻辑思维能力的重要手段

现今数学课本中的内容，集中外古今数学家研究之大成。数学知识纵连成线，横联成面，形成一个严密的网络体系，各知识点如同一个个网结点，彼此按一定的逻辑关系联系着并不断向外延伸。然而饭只能一口一口吃，课也只有一节一节上，分章分节使知识明晰化，条理化，但也容易割裂各知识点的逻辑联系。每个孤立的知识点犹如一捧明珠，学生手掬时往往也有部分散落在地。教师有责任“在授珠的同时也给学生一根可以把珠子穿起来的红线”。所以，数学教师不仅要把数学知识教给学生，还应引导学生构建数学知识网络，以便让学生牵一点而动全体，在数学领域纵横捭阖，融会贯通。为了引导学生构建知识网络，可以采用如下几个办法：

（一）在教学中注意数学知识点的纵向联系

在单元讲授的开始，先介绍本单元的知识线索，让学生明确学什么，顺序如何，要求怎样，重点在哪。例如，函数是高中数学的重头戏，不妨一开始就给出函数大单元的知识线索：函数的定义和表示（解析法、列表法、图像法）→函数的性质（函数值、定义域、值域、奇偶性、单调性、周期性、分段性等）→各初等函数（正比例函数、反比例函数、一次函数、二次函数、幂函数、指数函数、对数函数、三角函数、反三角函数）。重点在运用函数性质研究二次函数、指数函数、对数函数、三角函数及其图像。

在讲授某一数学定理、公式时，不能只要求学生“背熟、默出”，而要让学生习惯于运用数学的逻辑思维，环环紧扣，步步说理，弄清公式定理的来龙去脉，即怎样来，意义怎样，如何应用，最后在理解的基础上记忆、运用。

等比数列前n项和公式的推证用到了数列求和的一个重要方法——错项差法，可引导学生推证。

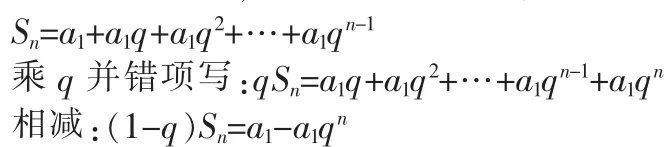
经过推证，学生既清楚了公式的来源、意义，易于记忆结果，也从中学到了求数列前n项和的一种方法。

（二）在教学中，重视数学知识的横向联系

知识点的横向联系，是指数学不同单元知识间的联系，即所谓综合性。加强知识点的横向联系，是构建知识网络的重要环节。

例如，在初等函数教学中，我们应让学生做到把变量、函数、图像、方程、不等式交织在一起，形成一个鲜明的网络体系，这样，将会收到使学生对数学融会贯通、运用自如的效果。

例如一道简单的不等式题：x2-2x-3＞0，求解。

设变量x，y，建立函数y=x2-2x-3

求二次方程x2-2x-3=0的判别式Δ=（-2）2-4·1·（-3）=16＞0

求二次方程x2-2x-3=0的根x1=-1，x2=3

画出y=x2-2x-3的函数图像（图略）

原不等式x2-2x-3＞0，即y＞0，图像在x轴上方部分对应的x的范围，即为不等式x2-2x-3＞0的解集。

由此，直接写出原不等式的解集为{x|x＜-1或x＞3}。

（三）注重知识的归纳与对比

人类智慧的提升，文明的发展，不在于单纯的劳动，而在于劳动实践后的反思和总结，以及在反思和总结基础上的开拓。学习一个单元，一个知识点，乃至做一道数学题后，教师都要引导学生进行归纳与总结，让学生形成习惯。归纳，就是要整理知识，整理思路，整理方法，强化思维的逻辑性。除用提纲式归纳外，可以在必要时应用表格。例如把圆锥曲线（包括椭圆、双曲线、抛物线）的标准方程、几何参数、图像等编列成表格是常用的归纳方法。其他数学知识，也可以做一些尝试。

另一个行之有效的方法就是对比。对比，也就是把两种相关联的数学知识的异同点进行比较，借以明晰概念，区分思路，巩固记忆。笔者曾尝试把“指数函数性质”与“对数函数性质”对比授课，也曾尝试把“图形法”与“坐标法”对比进行向量单元的教学，均收到效率高、学生掌握好的效果。

（四）有意识地引导学生逐步学会数学知识总结

知识总结，开始不妨由教师做，逐步引导学生自行总结，再放手让学生自己做。学生一旦形成了总结习惯，是终身受用的。

努力激发学生数学研究精神是培养学生数学逻辑思维习惯的关键

诸如前述，逻辑思维能力是一种素质，是成为创新型人才的基础。数学研究精神，也就是要多思，从多种角度去思考，分析和解决数学问题，并在这基础上生发、开拓、创新，形成数学逻辑思维习惯。不可讳言，中专学生比较缺乏数学研究精神。功利性地学数学固然不能培养数学逻辑思维能力；题海战术使学生忙于应付，结果是懂的重复做，不懂的仍不懂，也难以引发学生的数学研究精神。有时，精选的少量简单数学题，引导学生多角度分析，一题多解，多变，解题后反思和总结，却是引发学生研究精神、形成数学逻辑思维习惯的有效手段。

比如简单的参数不等式ax+b＞0（a，b∈R），求关于x的解集。

这是没有研究参数a，b的正、负、0所致。

正确解法是：ax+b＞0，由同解性质知ax＞-b成立接着要引导学生讨论a和b

当a=0时，即0x＞-b，左边必恒为0

当b＞0时，0＞负数，x∈R

当b≤0时，0＞正数，或0＞0，x∈Ø

可设置思考题：可否用图像法解？如何解？

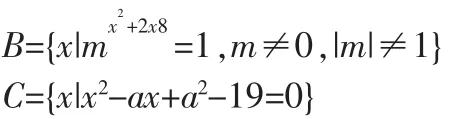
且A∩C≠Ø，B∩C=Ø，求实数a的值

本题的逻辑思维路线应是：

1.解出A，B：

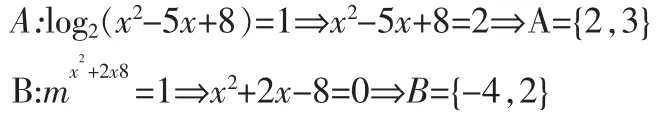
2.利用交集条件求C的部分元素

3.把x=3代入C求a

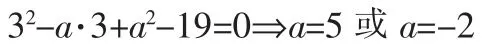
至此好像解完了，但漏去了检查结果是否符合条件，故有：

4.把a代回C检验

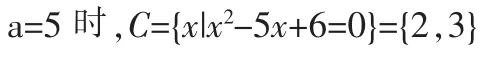
不符合条件B∩C=Ø，故舍去

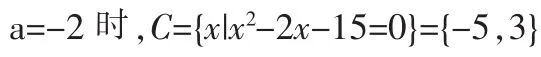
符合题设条件，综上得a=-2。

培养学生的数学逻辑思维习惯的教学心理和激励机制

培养学生的数学逻辑思维习惯是一项系统工程，除上述方面外，还需从学生的数学学习心理着手，适当设置使学生自觉养成数学逻辑思维习惯的激励机制。为此，在教学上应做到：

（一）循序渐进，复旧引新，化繁为简，化难为易，化抽象为具体，使学生易切入，明其理，可操作

学习，首先要有兴趣，有了兴趣，才能有注意，才能产生求知欲与学习的热情。中专学生学数学的最大障碍在于对数学的“畏难”心理。上述做法正是针对这种心理的重要方法。破除了“畏难”心理障碍，学生对数学发生了兴趣，进而才会“乐学”数学。

课本的内容，经过专家的审定，已是十分严密。然而教师的教学是一种再创造，教师应从具体学习者的实际出发，在大纲及教材统制下，合理调整教学方法，以使所教内容为学生易懂、会用。

例如，现行中等职业教育《数学》（基础模块）中，对函数是这样定义的：“在某一变化过程中有两个变量x和y，设变量的取值范围为数集D，如对于D内的每一个x值，按照某个对应法则f，y都有唯一确定的值与它对应，那么，把x叫做自变量，把y叫做x的函数，数集D叫做函数的定义域”。

这定义对于没有介绍“映射”概念的教材系统来说，应该说是完整与严密的。但从学生角度去想，这样的定义不易学，不易懂，不易记，更不好操作。教师很有必要把它分解开来，再让学生在理解的基础上记忆。笔者认为可作如下分解：（1）函数是两个变量间的关系，即变量x通过某种变换f变换为变量y，记作（2）当变量x取某一可能数值时，变量y有且仅有一个数值与之对应 （即在直角坐标上有且仅有一个对应点）；（3）x称为自变量，y称为x的函数，记作y=f（x）；（4）y=f（x）的具体解析式称为函数解析式或函数方程式；（5）当x取某一可能数值x=a时，对应的y值 （可从代入具体函数式中求出）称为x=a时的函数值，记作：y=f（a）；（6）使函数式有意义的自变量x的取值范围称为函数的定义域；（7）在函数的定义域范围内，函数y的取值范围称为函数的值域；（8）函数的定义域与值域可用区间符号表示。

在以上各点中穿插适当的例子，再回头读课本的定义，学生就明白易懂了。

（二）精选例题、习题

一题多变，逐步引导，由浅至深，由单一到综合要精选例题、习题，掌握好“习题有一定思考性又是大多数学生可解的”这个分寸，让学生有学习的成就感。不要追求高深难题，也不要用题海压迫学生学习。

（三）做好经常性的总结

一单元、一节课授毕要总结，一题解完也要梳理思路，对比正误，明晰方法，让学生有法可依，有路可循，有念可悬，有境可拓。

[1]张大均.教育心理学[M].北京：人民教育出版社，2005.

[2]邱亚明，崔永红.职校生数学学习障碍成因分析[J].职业教育研究，2010，（10）.

[3]鲁军兵.职高数学课激趣方法初探[J].职业教育研究，2010，（10）.

[4]李文林，任辛喜.数学的力量——漫画数学的价值[M].北京：科学出版社，2007.

[5]熊亚飞.创设问题情境，培养数学学习兴趣[J].中等职业教育，2010，（9）.

[6]聂新桥.读刊有感——引领学生跨越思维的障碍[J].数学教学，2010，（10）.

[7]黄另竹.对中职学生数学学习兴趣培养的探讨[J].中等职业教育，2010，（9）.

G710

A

1672-5727（2011）11-0106-03

严亚娣（1961—），女，湖北武汉人，中山市中等专业学校教师，中学高级教师，研究方向为中职数学教学。