基于卡尔曼滤波器的频率源远程校准技术研究

左建生，董 莲，陆福敏，张树生

（1.上海市计量测试技术研究院，上海 201203；2.中国计量学院机电学院，浙江 杭州 310018）

0 引 言

目前时间频率源的远距离校准成为研究的热门问题，如何利用GPS共视法更好地实现远距离的校准，数据处理和计算方法是提高精度关键步骤之一。GPS共视法就是在A、B两地同时跟踪同一颗卫星，在相同的时刻跟踪相同的卫星，用相同的软件处理方法处理数据，将两地的GPSREF作为钟差，从而得出A、B两地的相对频率偏差。但是在GPS接收机接收过程中，由于受到电离层、对流层、天线相位中心角、电缆、实验室温度环境[1]等一系列外在因素的影响，给校准结果带来很大的误差。如果直接根据做差拟合计算得出结果作为相对原子频标频率差，进而算出相对频率漂移率和相对频率准确度，会给实际结果带来较大的影响。所以这就要求对钟差数据进行滤波，尽量消除外在因素的影响。

目前国际上通常采用的是Vondrak滤波方法对钟差数据进行滤波。该文在LabVIEW软件平台上实现了对钟差数据的卡尔曼滤波，方法简单易行，通过计算结果显示滤波前与滤波后的曲线对比。结果表明，滤波后的曲线更平滑，结果更精确，更能接近实际结果。

1 基于钟差数据的卡尔曼滤波模型

一般振荡器的输出信号可以描述为

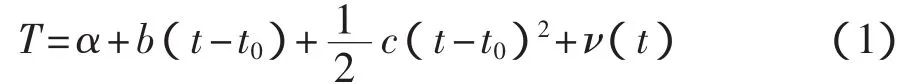
式中：α——初始相位；

b——频率偏移；

c——频率老化系数；

ν（t）——原子钟的噪声[2-3]。

一般情况下，在太阳、大气的扰动及接收机附近的强干扰影响下，来自GPS接收的钟差比对数据中，由于GPS信号在传输过程中受电离层、对流层等的影响，钟差数据是一个离散的数据序列，包含很强的噪声，其allan方差可能是信号的几倍甚至几十倍，所以钟差数据序列并不能真实反映实际性能指标。卡尔曼滤波（Kalman）算法是一个不断预测和修正的过程，无需储存大量的钟差数据，当接收到新的观测值时，它可以通过前一个采样时间的估计值和观测值来预测当前值。利用卡尔曼滤波选择a、b、c 3个状态建立常加速运动模型，假设状态变量的概率近似服从均匀分布，用输入为白噪声的相关模型来表示。由于原子钟差的运动特性，可以采用初始非零均值和修正瑞利分布的相关模型代替一般的滤波模型[4]，再进而对其离散。

离散动态系统[5-6]为

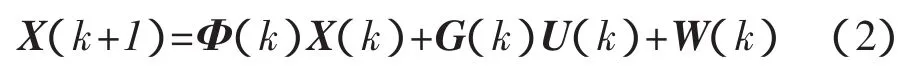
其中：

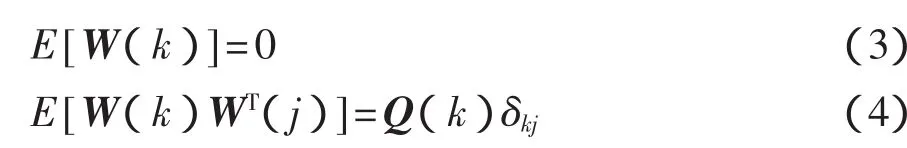
量测方程为

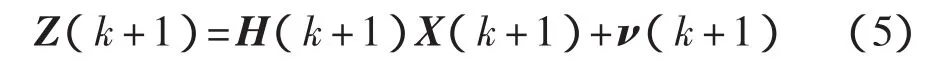
其中：

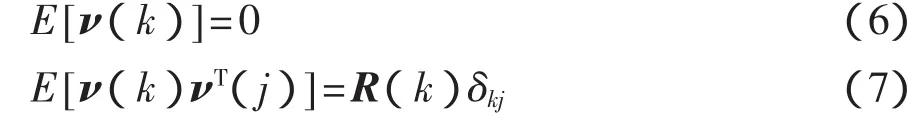
在共视比对系统中得到本地原子钟间的钟差REFGPS1，通过对异地接收机数据的可共视记录的REFGPS2项作差，可得到含噪声的钟差数据序列。该连续数据序列中2个钟差数据的时间间隔为一次全长共视的时间960 s[7]，其观测量是含噪声的钟差数据，必须进行滤波处理才能提高比对精度。通过建立不变离散系统的状态空间用式（2）和式（5）进行表述，确定初始状态后，可进行递推的方法得到状态方程的解。假设在k时刻钟差真实值用X（k）表示，其滤波值为X^（k/k）和X（k）的协方差矩阵为P（k/k），这样滤波方程可表示如下：

Kalman滤波的状态预测方程为

预测协方差矩阵为

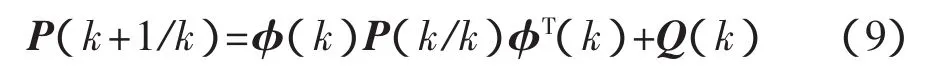
量测预测值为

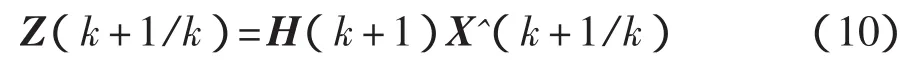
信息协方差矩阵为

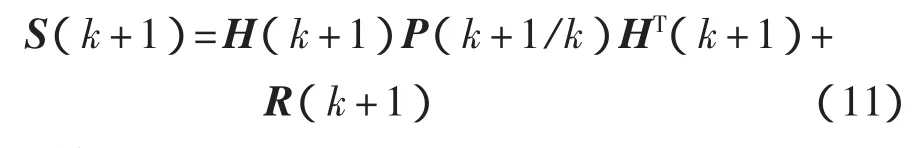
增益矩阵为

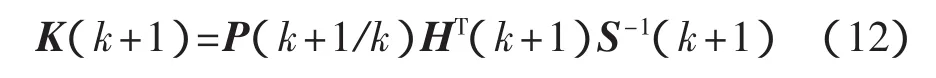
状态滤波值为

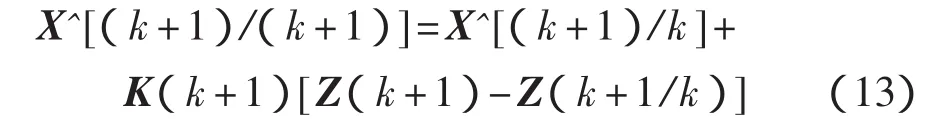
滤波协方差矩阵为

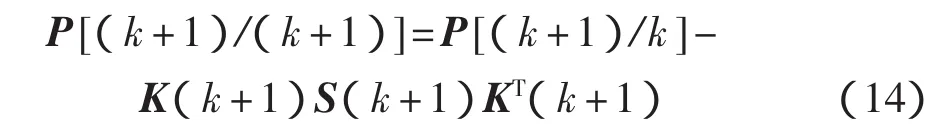
2 Kalman滤波器在LabVIEW中的实现

使用LabVIEW软件设计的Kalman滤波器程序相对简单、易懂[8]，既可实时观测到读取的钟差数据序列，又可实时观测到钟差数据与滤波数据之间的对比。当钟差数据偏差较大时，就用该时刻的Kalman滤波估计值来代替当前误差较大的接收值[9-10]，从而给出更精确的相对频率偏差、相对频率漂移率、相对频率稳定度以及相对频率准确度等。

（1）从计算程序中读取共星、共时情况下得到的钟差数据序列。建立系统模型，对滤波参数进行设置。模型噪声和观测噪声的协方差矩阵取值，应根据实际数据，进行尝试比较[11]。经在程序中反复比较得出：当模型噪声和观测噪声的协方差矩阵取值为 Q=[0.025]、R=[1]时，滤波效果是最好的，滤波值也是比较接近实际结果。

（2）对当前时刻的钟差数据与滤波估计值进行比较，当钟差数据偏差较大时，就用当前的滤波估计值来代替钟差数值，这样处理的数据更加准确。对滤波出来的数据再进行拟合计算，会得出更加准确的相对频率漂移率。

（3）图像显示和数据保存，将原钟差数据序列和对应的滤波估计值都显示在图像上，同时将数据保存到数据库中。钟差数据序列和滤波数据分别保存，方便校准方和被校准方查看数据、校准结果以及剔除的偏差数据。

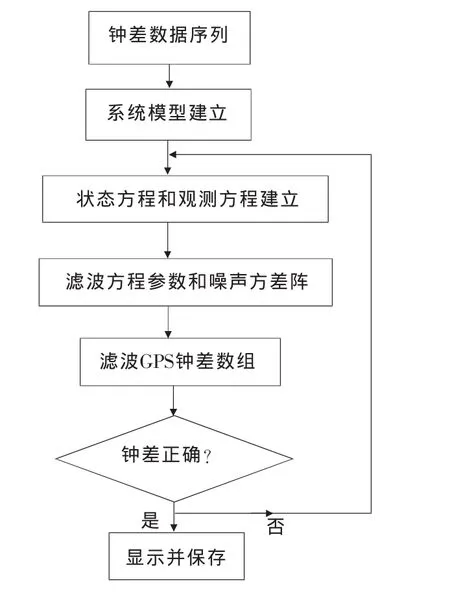
图1 卡尔曼滤波流程图

Kalman滤波流程图如图1所示，程序设计如图2所示。

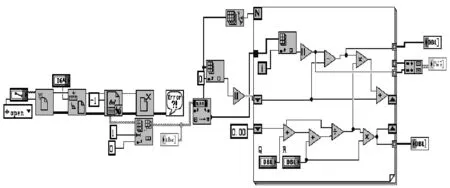
图2 卡尔曼滤波器程序

3 比对结果

2009年11月22日到12月22日的数据，与中国计量科学研究院进行了远程氢原子校准的数据，用编的软件对钟差数据序列进行滤波，表1是部分原始钟差数据序列滤波前与滤波后进行的对比。从表中1可以看到滤波后数据更加趋近实际值，剔除偏差较大的数据可以得到更加准确的钟差数据，有利于得出更加准确的校准结果。

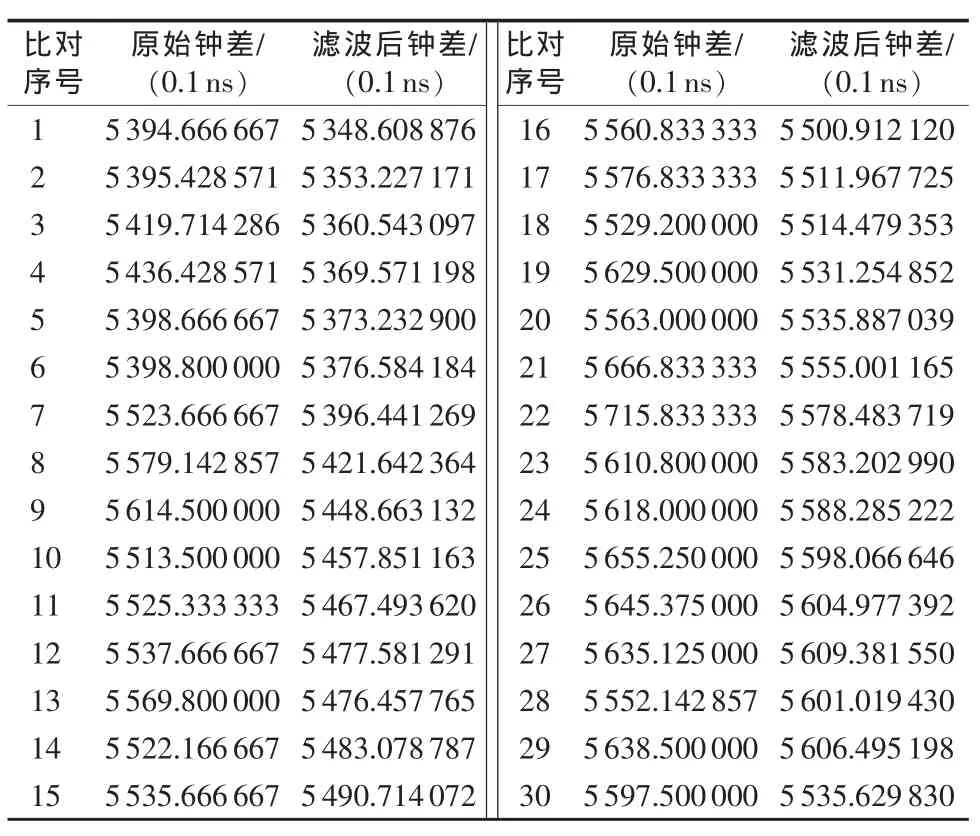
表1 滤波前后钟差数据对比

在图3中，虚线代表滤波前钟差数据序列，实线为滤波后的钟差数据序列。从图3中，可以看到滤波之后的钟差数据相对集中，波动不像原始钟差数据那样波动较大，从而使结果更加准确。

4 结束语

该文通过对卡尔曼滤波理论的深入研究，并结合时间频率标准器在远距离校准中存在的误差问题，用LabVIEW软件建立了Kalman滤波模型，通过对离散钟差数据序列的处理和预测，更加准确地反应频率源的性能。试验数据表明，选择参数合理，有效地降低了噪声造成的误差，从而提高了校准精度。

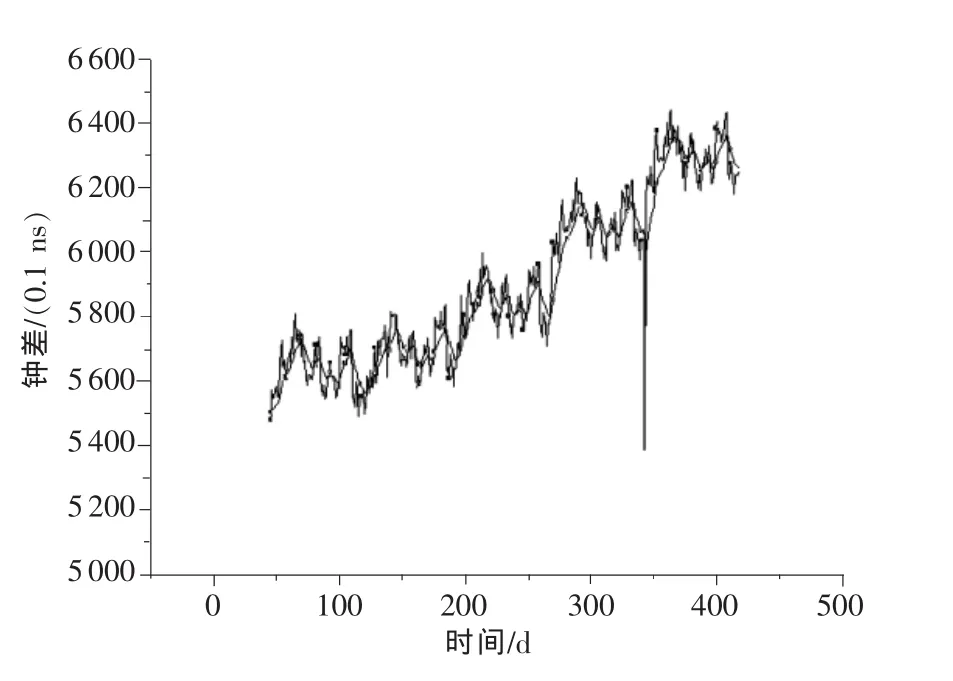
图3 卡尔曼滤波图

[1] 张守信.GPS卫星测量定位理论与应用[M].长沙：国防科技大学出版社，1996.

[2]王敏.GPS数据处理方面的最新进展及其定位结果的影响[J].国际地震动态，2007，343（7）：3-7.

[3]胡锦纶.多通道GPS定时接收机的测量数据处理方法和结果比较[J].中国科学院上海天文台年刊，2000（21）：134-139.

[4] 闫瑞丽.利用GPS信号驯服高稳晶振的误差分析[J].仪表与计量技术，2010：41-42.

[5] 范洪达，李相民.卡尔曼滤波算法的几何解释[J].火力与指挥控，2002，27（4）：48-50.

[6] 刘婵媛，陈国光.基于GPS的卡尔曼滤波技术研究[J].弹箭与制导学报，2006（4）：110-112.

[7] 杨旭海，胡永辉，李志刚，等.GPS近实时共视观测资料处理算法研究[J].天文学报，2003，44（2）：204-214.

[8] 陆文娟，王永吉，徐建军.基于卡尔曼滤波器的管道泄漏检测技术研究[J].科学技术与工程，2009，9（18）：5469-5471.

[9]杨坤明.组合导航系统的卡尔曼滤波器的设计[J].西华大学学报：自然科学版，2005，24（4）：86-88.

[10]白俊卿，卫育新.车载SINS/GPS组合导航系统的在线标定算法[J].电子设计工程，2010，18（2）：89-90.

[11]吕艳梅，李小民，孙江生.高动态环境的GPS信号接收及其算法研究[J].光电与控制，2006，13（4）：24-27.