CRC算法的应用理论研究

欧海文 李起瑞, 胡晓波 赵静

1 西安电子科技大学通信工程学院 陕西 710071

2 北京电子科技学院 北京 100070

3 北京中电华大电子设计有限责任公司 北京 100102

0 引言

在通信领域，由于数据在传输和存储过程中受到各种干扰，使信号码元发生变化，所以需要进行数据校验以确保数据的完整性。循环冗余校验CRC(Cyclic Redundancy Code)由于其具有检错效率高、原理简单、易于实现的特点得到了广泛的应用。

1 CRC算法基本原理

CRC校验码由分组线性码的分支而来，其应用主要为二元码组，由一个生成多项式(最高次幂为 r)产生，r次的生成多项式可产生r位的冗余码，所有码字的运算是封闭的。

设每个信号码元的序列为m={mn-1mn-2…m1m0}用多项式表示为：

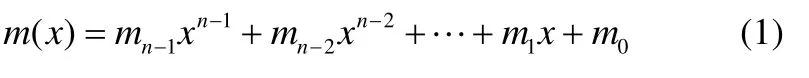
CRC编码步骤可归纳如下：

设生成多项式g(x)的最高次幂为r，上式两端乘以xr得：

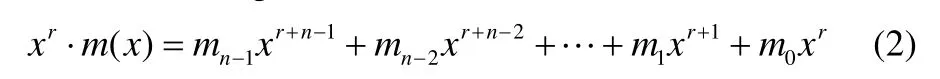
用 g(x)模 2 除xrm(x)，得商Q(x)和余式r(x)：

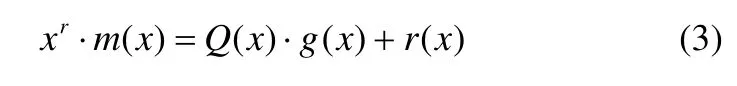
编出的码为：

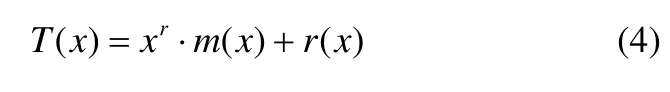
可得输出码序列为：

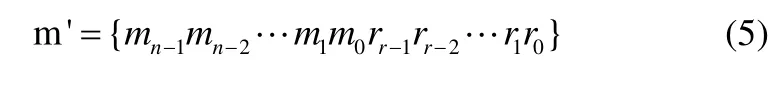
接收方校验数据有两种方法：

(1) 对原始数据采用与发送方同样的生成CRC校验码的方法生成r'(x)，然后与r(x)比较，相等则校验通过，否则认为数据传输出现差错。

(2) 对接收的数据计算m'(x)≡0modg(x)是否成立，成立则校验通过，否则认为数据传输出现差错。

2 CRC的INTI和XOROUT值

定义 1：函数CRC(INIT,m)表示以INIT为寄存器初始值，输入数据为 m计算 CRC校验值，默认CRC(m)=CRC(0,m)。

性质1：∀m∈{0,1}r,CRC(m,m)=0

性质2：∀mi∈{0,1}r,∀ai∈{0,1}∀

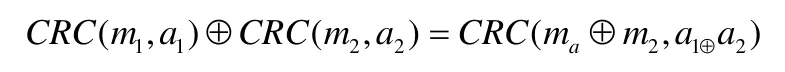
性质3：∀m，a∈{0,1}r,CRC(m,a)=CRC(a,m)

CRC算法虽然选择相同的生成多项式，但开始时寄存器中设置的初始值不同得到的CRC结果也不同。初始值对CRC算法的结构性能没有任何影响，可以任意设置，通常为了使得传输数据最前面的 0能够正确传输，会将 INIT设置为0xFFFF同时，出于相同的目的会在CRC计算完成后将寄存器中的结果异或上一个XOROUT=0x FFFF值，然后结果输出，函数表示为：CRC(m)=CRC(INIT,m)⊕XOROUT 。

3 CRC的生成多项式

生成多项式在 CRC校验中具有决定性的作用，应该指出并非任何一个多项式都可以作为生成多项式，文献[1, 2, 3]等给出了选择生成多项式的具体要求和准则。目前国际上已经公布了几种 CRC生成多项式的标准供我们使用，例如CRC-CCITT=x16+x12+x5+1，通常国际上用其反射多项式表示为0x8404，且已证明好的生成多项式的反射生成多项式也是好的生成多项式。

4 CRC可校验数据长度和性能

CRC可校验的数据位的长度是可变的，生成多项式g(x)或其某个因子为 t次本原多项式时，我们将数据位长度以2t-1为界分两种情况讨论。

4.1 缩短循环码

CRC在本质上是一种缩短循环码，在(n-i,k-i)循环码的2k个码字中挑选出前i bit为0的码字作为(n-i,k-i)缩短循环码的码字，它的码集是(n, k)循环码集的子集，所以它是一种系统循环码，当数据位长 n小于 2t- 1时，除了不具有循环码的循环性外具有循环码的全部特性。

根据有限域相关知识，生成多项式g(x)或其某个因子为t次本原多项式时，这个本原多项式能够整除的xn+1中，n的最小值是2t-1，它能产生的循环码长就为 2t-1。

以 CRC16为例，它的生成多项式g(x)=x16+x12+x5+1=(x+1)(x15+x +1)其中(x15+x+1)是本原多项式，能够整除的xn+1中，n的最小值是 215-1=32767，所以原始循环码是(32767, 32751)循环码。它保留了原始循环码除循环性的特性，也决定了用 CRC16校验时的最大信息长度平凡情况下不超过32751。

4.2 扩展缩短码

在GF(2)上，生成多项式g(x)或其某个因子为t次本原多项式时，这个本原多项式能够整除的xn+1中，n的最小值nmin=2t-1，当g(x)能整除xnmin+ 1时，g(x)定能整除xn+ 1，其中n=m∗nmin，这样由g(x)生成了一个码长大于2t-1的(n,k, r)循环码，然后从中挑选出前n-N位为全0的信息位得到(N, N-r, r)扩展缩短码，其中(m-1)nmin≺N≤n 。

5 CRC算法性能

CRC作为缩短循环码时的性能研究已经得到了较好的解决，CRC的检错性能由最小码距和编码本身的特性决定，以CRC-CCITT为例，由于其最小码距为4，则：

(1) 能纠正1bit的随机差错；

(2) 能100%检测出奇数个差错；

(3) 能100%检测出任意的2bit的随机差错；

(4) 能 100%检测出小于等于生成多项式码重dmin-1的随机差错；

(5) 能l00%检测出长度小于等于校验位长r的单个突发差错；

(6) 能以1-2-(r+1)的概率检出长度为r+1的单个突发差错；

(7) 能以1-2-r概率检出长度大于r+1的单个突发差错；

扩展缩短码和缩短循环码一样是线性分组码，易知它们具有相同的平均不可检错误概率，但二者的差错检测性能仍有稍微不同。

汉明码校验矩阵包含r重的所有码，任何两列是线性无关的，校验矩阵的线性相关性决定了(n, k)线性码分组码的最小距离，汉明码最小距离等于 3。缩短码校验多项式的列数小于汉明码校验多项式的列数，在此情况下缩短循环码的最小距离不小于 3。扩展缩短码校验多项式的列数大于汉明码校验多项式的列数，其校验矩阵至少有两列是线性相关的，所以扩展缩短码的最小距离一定等于2。

所以，CRC作为扩展循环码时将不能100%检测随机2bit错误，同样也不能纠正随机1bit错误。

6 CRC的实现及应用规范

目前，CRC的计算方法主要有串行和并行两种，实现方式也可分为软件实现和硬件实现，大量的文献对此进行了研究，但鲜有文献介绍CRC的应用规范，这里以CRC-CCITT为例对各个参数进行说明(如表1)。

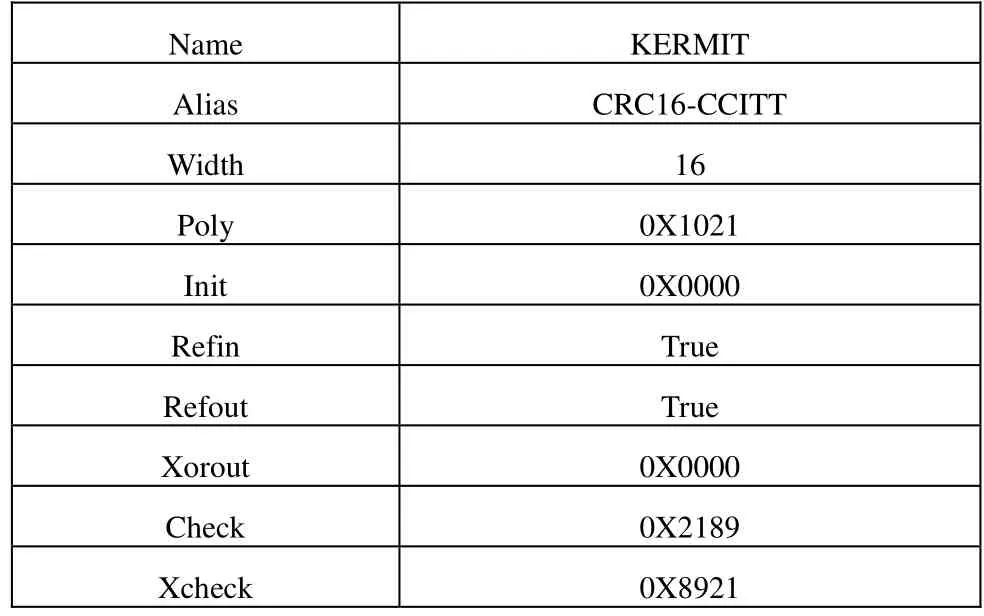
表1 CRC16-CCITT

其中各参数意义为：

Name：名称。

Alias：别名。

Width：校验位长度，设为r。

Poly：生成多项式，以十六进制表示，最高位省略。

Init：初始化值，以十六进制表示。

Refin：设置为布尔值。

(1) False取信息多项式的反射多项式，即将信息位反序输入；

(2) True正常输入。

Refout：设置为布尔值。

(1) False运算完毕后寄存器中的 CRC值直接进行Xorout步操作；

(2) True运算完毕后寄存器中的CRC值进行反序操作；

Xorout：一个r比特长的十六进制值，在Refout步骤进行后与寄存器中CRC值进行异或操作。

Check：ASCII字符串“123456789”即[31 32 33 34 35 36 37 38 39]的CRC校验值，主要用于验证以上参数设置的正确性。

Lcheck：ASCII字符串“123456789”后面附加上“9”的二进制形式即[31 32 33 34 35 36 37 38 39 09]的CRC校验值。

Xcheck：ASCII字符串“123456789”的CRC输出值，但高低位字节交换顺序。

7 结束语

CRC作为一种在通信领域中广泛应用的检错方案，之前被大量文献进行了较好的研究，本文补充了现有文献中的空白，解决了在实际应用中常碰到的如何设置寄存器的初始值及如何选取生成多项式的问题；同时，通过分析不同长度下算法性能差异提出了 CRC算法对校验数据长度没有限制的观点，进一步指出 CRC作为扩展循环码时平均漏检概率上限值虽未改变，但由于最小码间距改变成 2，因此将不能100%检测随机2bit错误，也不能纠正随机1bit错误的观点。

CRC曾被考虑作为一种Hash算法，但由于它具有一定的漏检概率而未被采用。其实，CRC也存在着逆运算，即由校验码可以倒推出信息码或信息码的部分信息。对于CRC(INIT,m)=r，若INIT和r已知，显然，当信息码长度小于等于校验码长度时，二者成一一对应关系，此时可以通过查表法倒推出信息码，否则不能惟一确定信息码。因此，已知INIT和r求解m或已知r, m求解INIT是一个值得我们去研究的有趣问题。

[1] 马吉明,魏艳.探究缩短循环码性能与生成多项式的选取.通信技术.2008.

[2] 杨杰,朱建锋,安建平.无线传输中的循环冗余校验码纠错应用扩展.北京理工大学学报.2005.

[3] 瞿中,袁威,徐问之.CRC算法在计算机网络通信中的应用.微机发展.2002.

[4] 王新梅,肖国镇.纠错码－原理与方法[M].西安：西安电子科技大学出版社.2001.

[5] 周秦英,王新梅,葛晖.CRC在中扩展缩短码的设计与性能分析.西北工业大学学报.2004.

[6] 朱荣华.一种 CRC并行计算原理及实现方法.电子学报.1999.

[7] 蒋安平.循环冗余校验码(CRC)的硬件并行实现.微电子学与计算机.2007.

[8] Martin Stigge, Henryk Plotz, Wolf Muller. Reversing CRCTheory and Practice.HU Berlin Public Report.2006.

[9] Ross N. Williams. A painless guide to CRC error detection algorithms.www.cse.sc.edu/~jimdavis/Courses//crc-Ross.pdf.1993.