基于双目视觉的接触线几何参数检测系统优化设计

潘雪涛，谈少华，渠立山，张美凤，蔡建文

(常州工学院光电工程学院，江苏常州 213002)

电力机车接触导线几何参数主要是导线高度、拉出值、磨损创面宽度[1]。传统的人工检测以及检测车检测都存在着极大的局限性，危险大、效率低，不能满足实时检测的需要。近年来，上海铁路科研所、西南交通大学、大连交通大学的科研人员提出采用机器视觉技术，基于视差和光学三角原理[2]对接触线进行空间定位，从而得到拉出值、接触线高度和磨损等参数。这些研究集中在测量原理、系统总体设计或接触线图像信号的采集与处理等方面[3～5]，而对测量系统的结构设计并没有深入研究。但实际上双目视觉测量系统不同的布站方式，不同的结构参数，空间目标的探测精度会随之发生变化[6，7]。因此在设计测量系统前，结合实际条件和设计指标对系统的各项参数进行优化设计是可行的，也是十分必要的。

1 导线磨损面边缘定位精度分析

1.1 导线磨损面边缘空间坐标表达式

如图1所示，当光源照射到磨损后的接触线，磨损面与其他部分的光反射率存在明显的梯度。由两摄像机获取视场内导线图像，利用图像处理算法提取磨损面边界点A和B的空间坐标值后即可计算出导线几何参数。因此几何参数测量的关键是磨损面边缘点的空间坐标探测精度。

图2为双目立体视觉交汇测量原理图。设两摄像机光敏面尺寸均为2T，成像镜头Lens的焦距均为f，两光敏面中心间距为2L，交汇仰角(即光轴与y轴夹角)均为 α(0＜ α＜ 90°)。若磨损面边界点 A(x，y)在摄像机上对应成像点的坐标值分别为x1、x2，则根据几何关系可得其空间坐标表达式如式(1)、(2)，同理可得 B 点坐标值[6]。

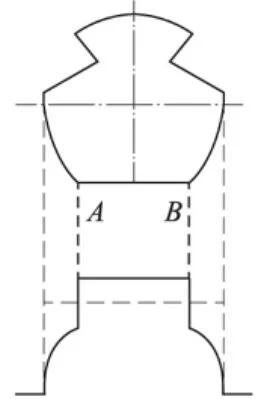
图1 磨损导线反射光强度曲线

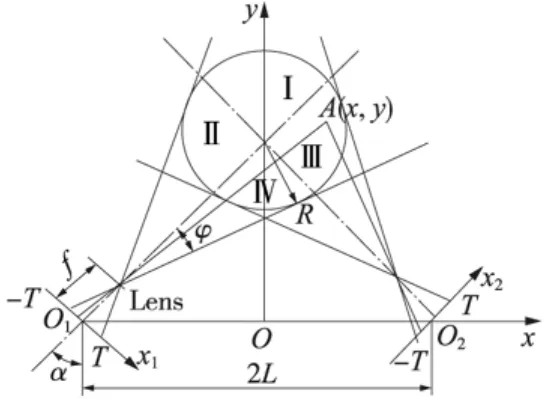
图2 双目立体视觉交汇测量原理

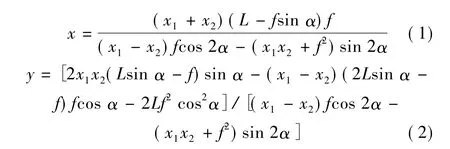
1.2 空间目标定位精度分析

1.2.1 坐标测量的有效视场

被测点必须落在两摄像机均能同时观察到的区域，这一区域称为有效视场。xoy平面中，在交汇测量的水平视场内作一内切圆，其半径R表示有效视场的大小。实际应用时，一般根据测量对象的实际条件，先确定R、T、f，然后得到L和α的关系

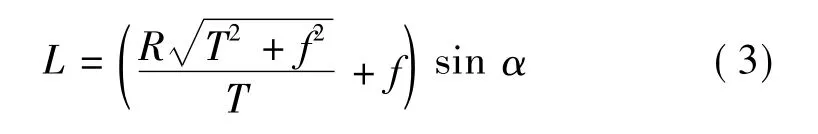
1.2.2 坐标测量误差分析

由式(1)、(2)可知，边界点 A的坐标值与 x1、x2、L、T、f、α5个参数有关，故坐标测量误差由这五个参数的测量误差决定。根据误差传递理论[8]，x坐标测量误差表示为

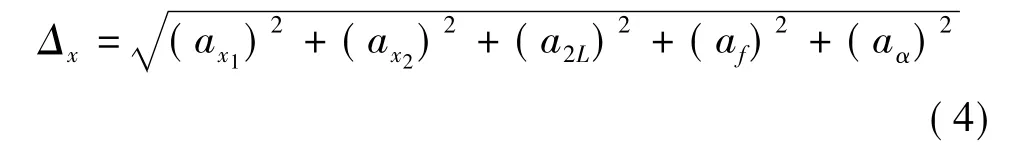
式中 ax1、ax2、a2L、af、aα为各误差分量。由式(1)对各参数求偏导可得

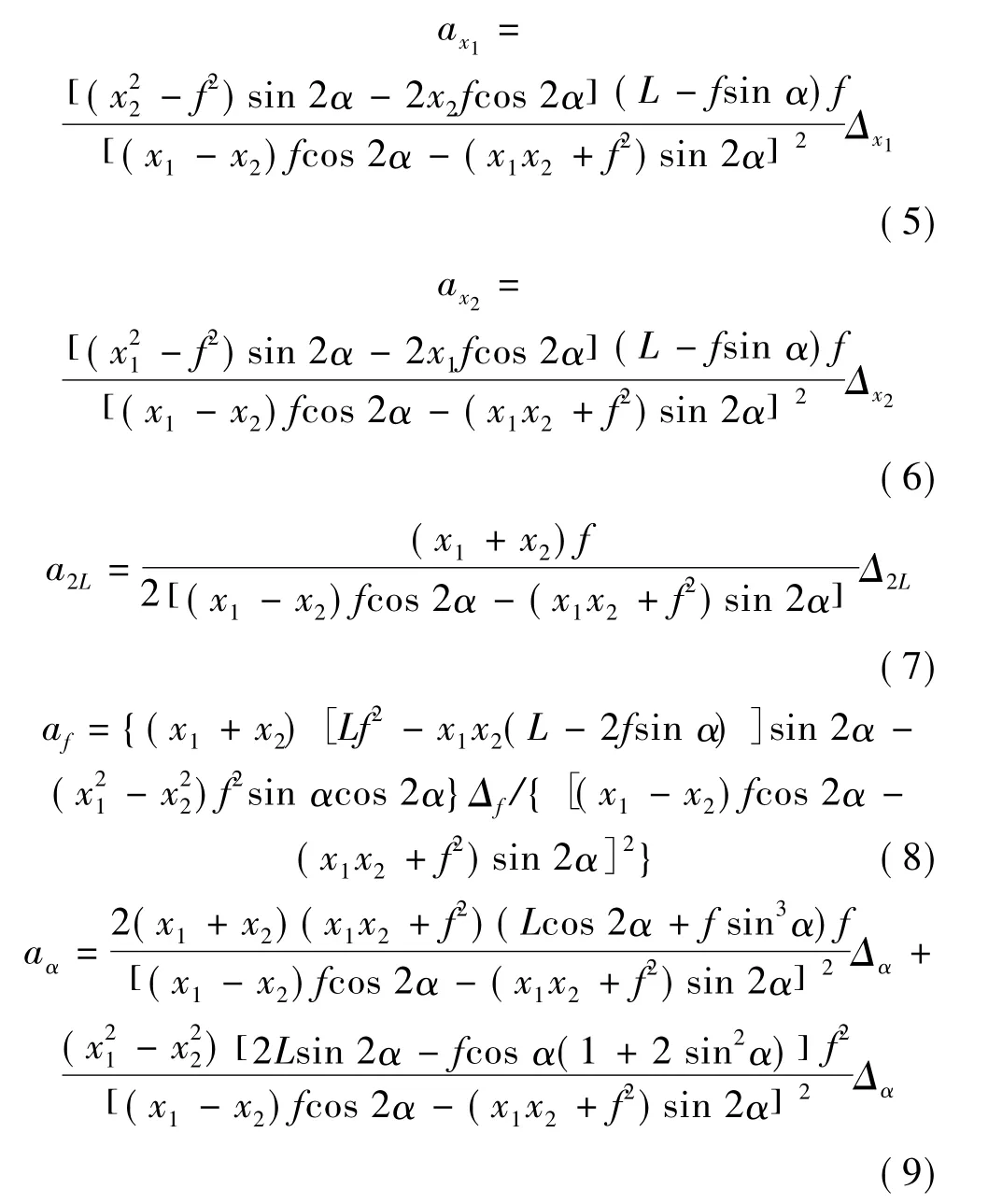
同理可求得y坐标测量误差

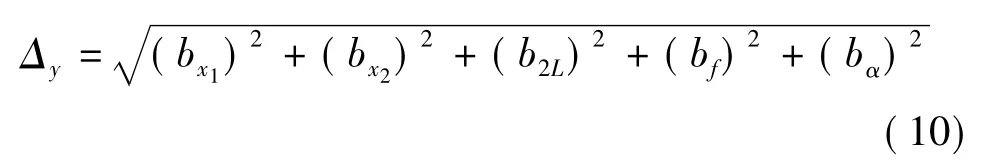
式中 bx1、bx2、b2L、bf、bα为各误差分量，具体表达式此处从略。

由上述表达式，利用MATLAB进行数值运算，可得坐标测量精度与各参数的关系，如图3所示。

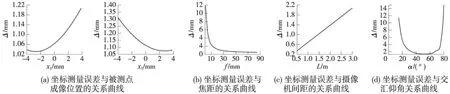
图3 坐标测量精度与各参数关系曲线

(1)有效视场内每点的坐标测量精度和该点成像位置有关，离基线(两摄像机间的连线)较远的区域误差值较大，离基线较近的区域误差值较小，如图3(a)所示。结合图2分析可知，有效视场内I区域的测量精度较差，而Ⅳ区域的测量精度较好。

(2)其他参数不变，像元间距越大，测量精度越低。保持摄像机摆放姿态不变，焦距越小，有效视场越大，测量精度越低;焦距增大，测量精度变高。当焦距大于20 mm，此时焦距变化对测量精度的影响已经较小了。测量误差与焦距关系如图3(b)所示。故测量系统宜采用长焦镜头(一般应大于25 mm)。

(3)其他参数不变，两摄像机间距2L越大，有效视场越大，测量精度越低。测量误差与摄像机间距L的关系如图3(c)所示。

(4)其他参数不变时，摄像机仰角α越大，有效视场减小，x坐标测量误差增大、y坐标测量误差减小，但综合误差增大，测量精度降低;反之，α过小，有效视场增大，y坐标测量误差迅速增大，导致测量精度降低。坐标测量误差与α的关系如图3(d)所示。测量系统的仰角应当在30°～70°选择。

2 测量系统结构参数优化设计

通过对坐标测量误差的理论分析和数值仿真可知，空间目标探测精度会随结构参数的不同发生变化，因此需要对结构参数进行优化设计，以确保达到测量要求。

2.1 接触导线几何参数测量实际条件及部分参数的选择

电力接触导线高度一般为5 650～6 200 mm，测量误差±5 mm;拉出值一般为300 mm，测量误差±2 mm;接触导线直径一般为10.19～14.40 mm，导线磨损创面宽度测量误差±2 mm;需要将测量装置安装于列车车顶进行实时测量。

根据导线高度和拉出值变化范围，选择有效视场内切圆的半径R=350 mm;根据测量精度要求，选择LIS1024高性能CMOS图像传感器，其相关技术指标为1×1 024像素分辨率，像素尺寸 7.8 μm×125 μm，光敏面尺寸7.988 mm×125 μm，则T=3.994 mm，Δx1=Δx2=ΔT=0.007 8 mm，x1、x2在－3.994～3.994 mm 区间变化;摄像机镜头焦距为30 mm，Δf=0.03 mm;一般列车车体宽度为3 100 mm左右，考虑到加工、安装调试方便，初步确定L≤1 450 mm(具体值由优化设计给出)，Δ2L=0.1 mm，Δα=3″。

2.2 优化设计思路

结合测量要求以及部分参数的设置，给出最优结构参数的确定条件:(1)有效视场范围内，综合坐标测量误差 Δ的最大值为最小，且满足要求(即 Δ≤2 mm);(2)L≤1 450 mm。流程见图4、图5。

2.3 优化设计结果

图4 优化设计主程序流程

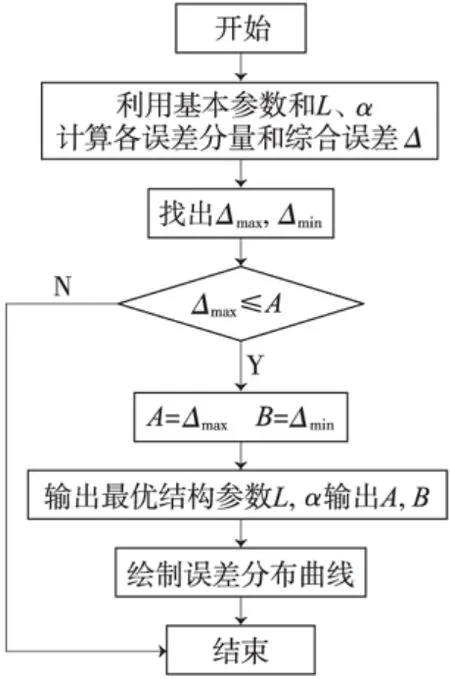
图5 优化设计子程序流程

程序计算得到的最优结构参数为α=36.1°，L=1 445.8 mm，此时有效视场内各点坐标测量误差在1.009 4～1.962 1 mm范围内变化，满足定位精度要求。因此测量系统机械加工参数为α=36.1°±3″，L=(1 445.8±0.1)mm。最优结构参数条件下各误差分量数值范围见表1。

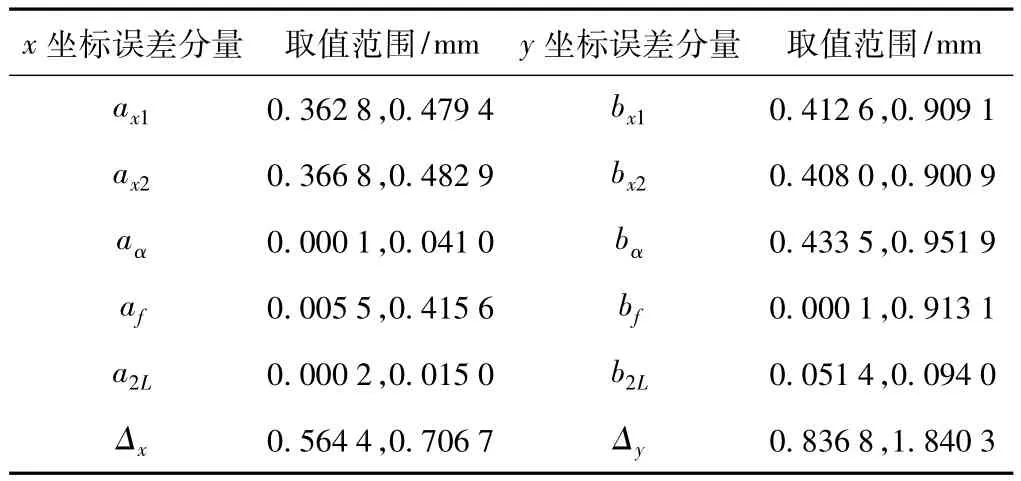
表1 各误差分量数值范围

有效视场内综合误差及误差分量的分布曲线如图6～图8所示。

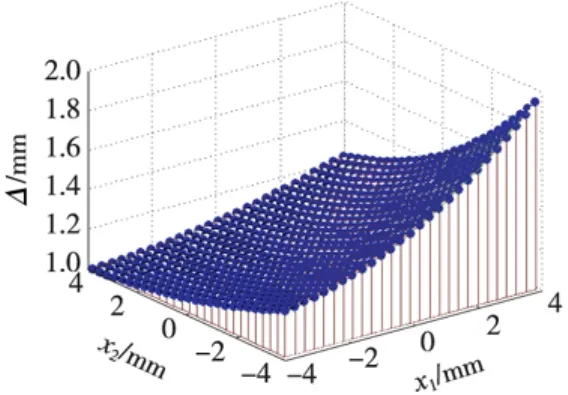
图6 最优结构条件下有效视场内坐标测量综合误差分布曲线

2.4 测量装置的基本结构

根据优化设计得到的结构参数进行样机制作，其结构如图9所示。这样的结构有如下优点:

(1)两摄像机反向放置，前面各摆放1个平面反射镜，这样摄像机交汇仰角的调整只需调整反射镜位置就可以了，大大减小了加工和安装的难度;

(2)这种结构增大了系统基线距，而系统的体积并不发生显著变化，质量更轻，便于固定。

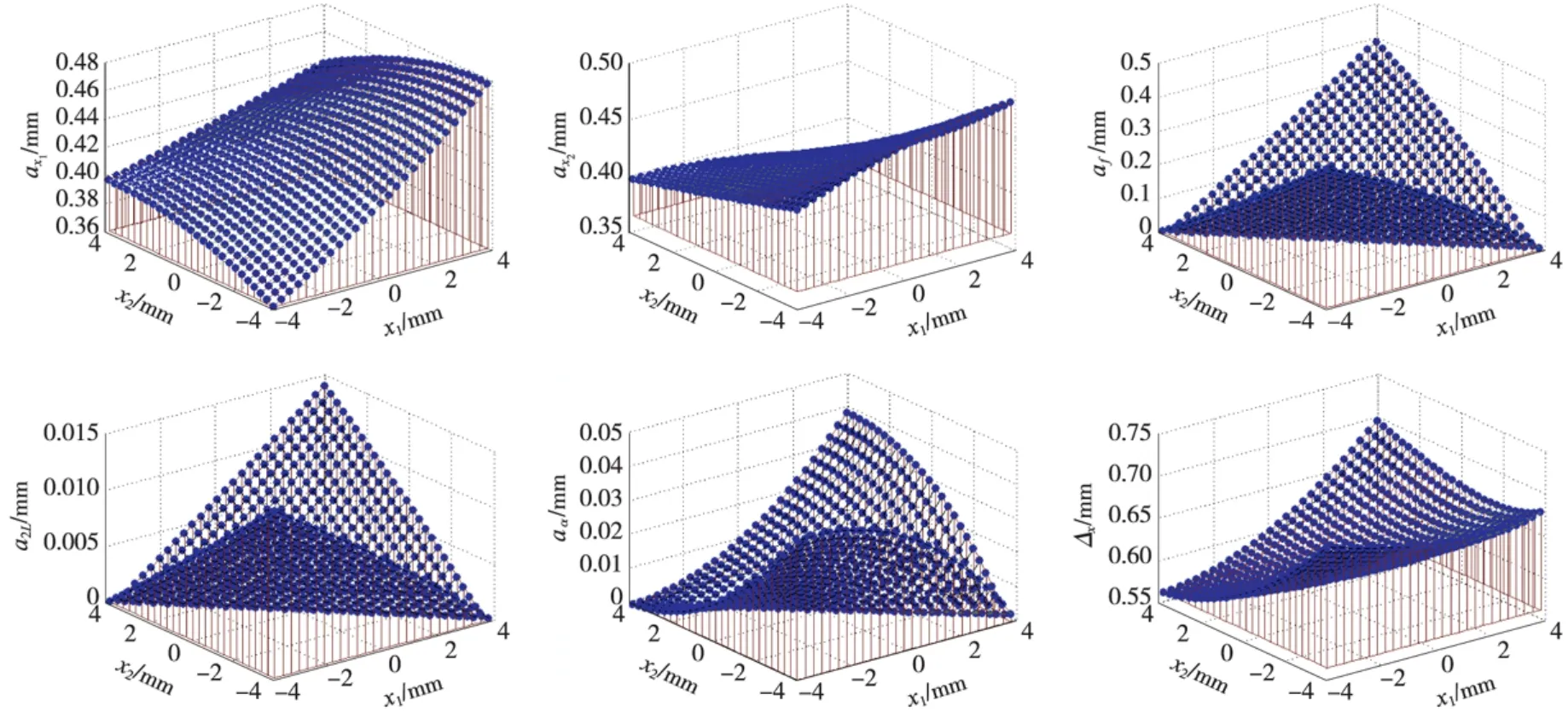
图7 最优结构条件下有效视场内x坐标各误差分量分布曲线

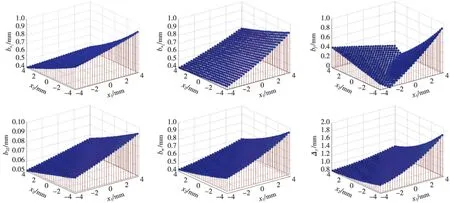
图8 最优结构条件下有效视场内y坐标各误差分量分布曲线

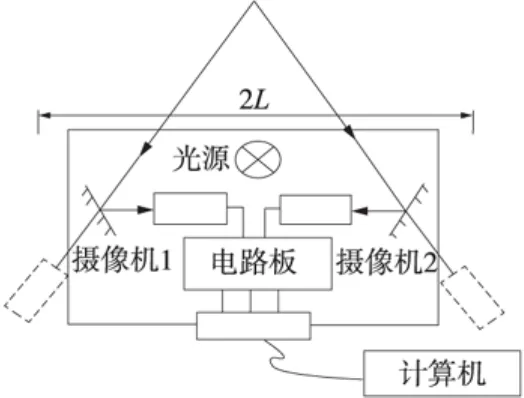
图9 基于双目视觉的接触线测量系统结构

3 结论

(1)根据优化设计得到的参数制作样机可以获得更高的定位精度，有效视场内离基线较远区域坐标测量误差较大，离基线较近的区域误差较小，使用时应根据接触导线的大致高度值合理安装仪器，尽量使其处于测量精度较佳的区域。

(2)在5个误差因素中，x1和x2对坐标测量精度影响最大，其次是f，再其次是L，α影响最小。成像点位置误差是随机误差，可通过选用高分辨率摄像机，或采用基于子像素的边缘检测技术对图像进行分析和处理，可有效减小像点的测量误差。间距L、焦距f和角度α的值及其偏差值是已知的，属于系统误差。在实际测量中可通过高精度标定最大限度的减小这些因素的影响。

[1]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社，2003.

[2]张广军.机器视觉[M].北京:科学出版社，2005.

[3]朱 挺，汤有福.线阵CCD摄像技术在铁路电力接触线高速检测方面的应用[J].上海铁道科技，2004(3):19－21.

[4]青 莉，高晓蓉.线阵CCD摄像技术在接触导线磨损检测中的应用[J].机车车辆工艺，2005(4):30－32.

[5]刘德仁，葛宰林，毕铁艳.电力机车接触线磨损数字图像处理研究[J].现代制造工程，2006(3):100－102.

[6]颜树华，吕海宝，周卫红，等.双CCD视觉传感器的建模及优化设计[J].光电工程，2000(4):30－34.

[7]钟堰利，贾福娟，丁 凌.双CCD交汇测量系统的设计方法[J].光学技术，2002(11):481－483.

[8]费业泰.误差理论与数据处理[M].北京:机械工业出版社，2005.