二维随机共振参数调节的图像处理
冷永刚,赵尔华,石 鹏,张 莹
(天津大学机械工程学院,天津 300072)
自从 1981年 Benzi等[1]研究古气象冰川问题提出随机共振(stochastic resonance,SR)概念以来,SR现象受到了广泛的关注.随机共振现象是一种非线性现象,它利用噪声的积极作用,使淹没于噪声中的弱信号得到共振加强,从而实现从强噪声干扰中检测微弱信号的目的.利用双稳SR技术处理一维信号的理论和实验研究在国内外已比较成熟,发表的相关文献也很多[1-3].双稳 SR对于淹没在噪声中的周期和非周期信号均具有很好地增强作用,即对于任意的一维序列,双稳 SR有助于突出其中的特征成分.随着随机共振应用研究的深入,其应用范围逐渐延伸到数字图像处理领域[4-8],如Ye等[4]利用双稳系统实现了图像直流分量的增强,另外在阈值系统中,Marks等[5]发现通过向图像添加适当强度的噪声可以使图像更加符合人的视觉特征,文献[6]提出了双稳SR能够改变信号的直方图分布,从而将双稳随机共振用于二维图像的处理.二维图像的SR处理方法通常是将二维图像先按行或列次序展开为一维数列,然后输入给双稳系统进行随机共振处理,此处称之为一维双稳SR.为进一步分析二维图像的随机共振现象,深入研究SR在图像识别和视觉理解过程中的作用,笔者以一幅经典的lena灰度图为研究对象,进一步完善一维双稳SR,并在此基础上提出图像的二维双稳SR方法.同时,由于系统参数的变化会引起势垒高度、势阱间距和粒子跃迁速率的改变[9],并使能量相对重新分布,使输出图像的质量不同,因此笔者在二维双稳随机共振的研究基础上,重点研究二维灰度图像 SR的参数调节规律及其输出图像质量的变化情况,并比较了一维SR和二维SR两种图像处理方法的优劣.
1 双稳态SR概述
在 SR的研究中,非线性双稳态系统模型通常由势函数表示,即

式中a和b为系统参数.在不考虑噪声的情况下得到一维非线性双稳系统的确定性动力学系统方程
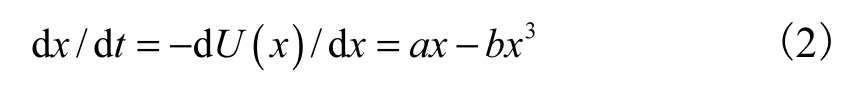
由定态方程d/d 0x t= 得到双稳系统的 3个解为1个不稳定的定态解10x= 和两个稳定的定态解从物理意义上理解,双稳系统的响应输出可以表现为一个粒子在双稳势阱内的运动,如图1所示.
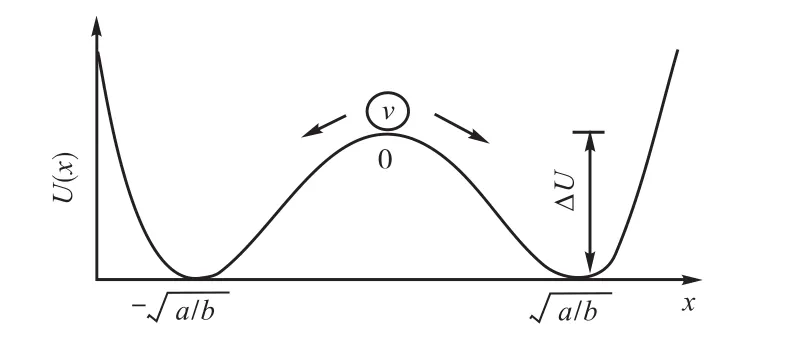
图1 非线性双稳系统势函数Fig.1 Non-linear bistable system potential function
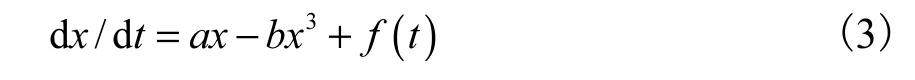
在噪声为零时,系统存在着临界值 Ac.当 A < Ac时,运动轨道将在附近进行局域的周期运动,只有在 A >Ac时,轨道才能围绕这两个定态吸引域做大范围的跃迁运动.当引入噪声后,在噪声帮助下,即使在 A <Ac时,系统仍可以在两定态解之间进行跃迁.
鉴于上述理论源自绝热近似[10]或线性响应理论[11],其研究对象必须符合小参数要求,即信号的幅度和频率以及噪声强度均比 1小得多.为了扩展双稳 SR的应用领域,文献[12-13]提出变尺度的方法处理工程实际中经常遇到的大参数信号,取得了较好的成效.此外,在一定条件下,噪声通过双稳系统对非周期信号的检测也具有积极的作用,以此产生和发展了非周期SR理论[14].
信号的 SR是利用双稳系统中随机力的非线性作用,利用噪声能量转移为信号能量来实现噪声的抑制和信号的增强,使系统的输出能够很好地跟踪信号的变化.图像是一种特殊的数据信号,它的像素值只能取正值,且在一定的范围内,超出这个范围,图像就会失真.由于图像信号的特殊性,因此笔者将图像的 SR限制在正势阱中,即研究图像二维 SR的单阱SR特性.
2 双稳态图像SR
2.1 图像二维SR原理
根据绝热近似理论或线性响应理论,系统的输入应满足SR的小参数要求.实际含噪二维灰度图像的灰度值范围通常是[0,255],为满足 SR 小参数的要求,将其归一化,即让输入图像灰度范围归一化为[0,1].这种归一化既满足 SR的小参数要求,又不会引起图像信息的丢失.
空间二维静态灰度图像可以表示为空间坐标x轴和y轴的函数 S = f( x , y),它是连续函数.图像处理时,必须对一幅灰度连续的图像进行采样.图像的采样是将在空间上连续的图像转化为离散点集的过程,把一幅连续的图像在空间上分割成mn×个网格,每个网格对应为一个像素点.图像是二维分布的信息,任一像素的灰度值都与周围的像素有关,所以采样是在x轴和y轴两个方向上进行.这里定义采样频率sf为单位尺寸内的采样像素点数,单位为像素/mm,于是图像 SR处理的计算步长为s1/h f= .根据变尺度SR方法[9-10],可以对计算步长进行缩放,选择合适的步长,以达到图像SR的最优输出质量.
二维灰度图像的SR可由连续两次一维SR来实现.其过程是,首先对输入的二维灰度图像进行归一化预处理,然后按行扫描得到一维序列并输入到双稳系统中进行 SR,将 SR输出序列按照行扫描的方式重新组成一个方阵,并将此方阵归一均化到[0,1]之间,得到一幅一维 SR 的图像.对这幅一维SR图像,按列扫描得到一维序列并再次输入到双稳系统中进行第 2次 SR,将共振输出得到序列按照列扫描过程的方式重新组成一个方阵,并再将这个方阵进行归一均化处理,就可得到二维 SR图像.图像二维 SR处理的基本原理过程如图 2所示.显然,上述过程改为先沿列后沿行进行二维 SR,其结果也是一样.

图2 二维SR图像增强算法原理示意Fig.2 Schematic diagram of two-dimensional SR image enhancement algorithm
需要说明的是,图像经过双稳 SR后,其结果矩阵不一定能够显示为一幅图像,需要将这个结果矩阵进行归一化处理,转换为灰度图像.这时的灰度图像其灰度值可能分布在某个很窄的灰度区域内,对比度很弱,图像细节不清晰.如果通过线性映射使分布密集的灰度区域重新均化到[0,1]之间,拉大图像的对比度,使图像的直方图均匀化,那么图像的细节又会变得清晰可辨.称这个过程为“归一均化”过程,具体实例过程如图3所示,它是将SR后的密集灰度区域[1.2,1.32]之间的灰度值归一均化到[0,1]之间.归一均化过程虽然造成了灰度区域[1,1.2]和[1.32,1.4]的信息丢失,但只是非常少的一部分信息丢失,可以忽略不计.

图3 SR图像的归一均化过程Fig.3 Normalizing and homogenizing of SR image
2.2 图像二维SR仿真
为观察图像的二维SR情况,从式(3)模型入手,以一幅经典的 lena灰度图为研究对象,通过仿真来考察双稳SR对图像及其直方图的影响.给出一组仿真参数:采样频率 fs根据变尺度 SR设为 fsr=10像素/mm,对应的计算步长为 h=1/fsr=0.1,系统参数a=5、b=10,输入信号为原始无噪图像.图像二维SR的数值计算采用四阶龙哥-库塔(Runge-Kutta)法,双稳输出图像的直方图及对应的图像如图4所示.
图4(d)是原始图像 4(a)的直方图.由图 4可以看出,二维双稳 SR改变了图像的直方图,使双稳响应图像的灰度和对比度发生了变化,灰度响应范围变小(见图 4(e)),集中在一个很小的范围内,对比度降低,几乎看不到图像及其细节信息(见图4(b)).但是对二维SR后的图像序列进行归一均化后,图像所包含的细节就会变得清晰(见图 4(c)),对应的直方图为图 4(f).表明二维 SR后,图像所含的信息量并没有减少丢失.当图像不含有噪声时,一维 SR与二维SR的结果类似,这里不再给出一维SR的图像.
下面给出含有高斯噪声的 lena灰度图的仿真例子.按照二维 SR方法,仍然取计算步长 h=1/fsr=0.1,系统参数 a=5、b=10,向标准 lena灰度图中添加均值为0、方差为0.4的高斯白噪声.其双稳SR响应图像的直方图及对应的图像如图5所示.
作为对比,图 5给出了一维 SR图像和二维 SR图像.由图 5可以看出,SR可以有效滤除图像中的噪声,使图像变得清晰,而且比较图 5(b)和(c)可知,二维SR图像比一维 SR图像噪声量明显减少,具有更清晰的效果,有更好的图像输出质量.因此,二维SR比一维SR具有更好的滤除噪声的效果.

图4 无噪图像的SR结果与直方图Fig.4 SR image and corresponding histogram of image without noise
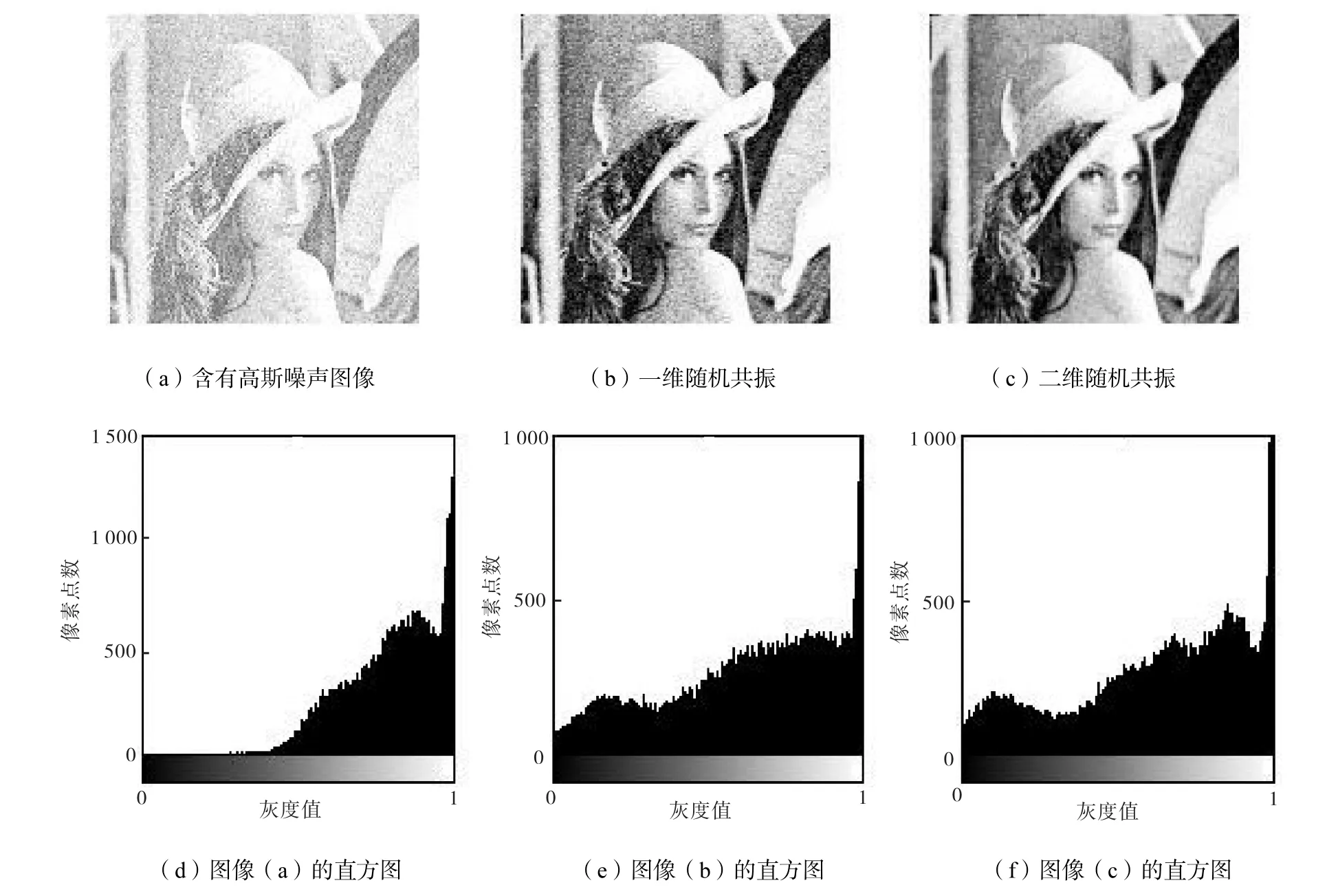
图5 含噪图像SR结果与直方图Fig.5 SR image and corresponding histogram of image with noise
3 参数变化对二维SR图像的影响
二维 SR图像的处理效果与双稳系统参数 a、b以及变尺度SR步长h密切相关.先固定SR计算步长,讨论双稳系统参数对二维SR图像质量的影响,然后再考察SR步长对二维SR图像质量的影响.
3.1 双稳系统参数对二维SR图像的影响
对于给定的一幅含噪图像,二维 SR处理效果的好坏可以通过对二维 SR图像与标准参考图像进行比较判断.图像质量的评价标准有主观评价和客观评价.主观评价主要是利用人的视觉进行评价,客观评价(即图像的逼真度)是一种定量的评价标准.图像的逼真度既可以用被评价图像与标准参考图像之间相似程度表示,也可以用被评价图像与标准参考图像之间的偏离程度表示.本文中主要研究客观评价的这两种判别方法.
图像的相似程度可用相似系数 C ( X , Y )表示,其表达式为[15]
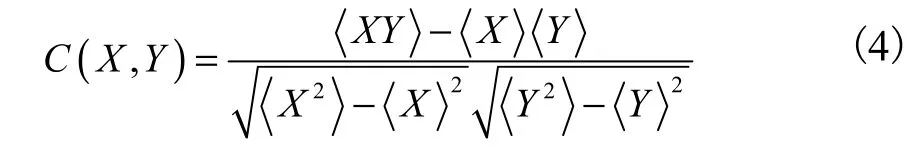
式中:X为标准参考图像,归一化到[0,1];Y为二维SR图像; ⋅表示图像的平均值;
图像的偏离程度用偏离系数(即均方根误差)表示,其表达式[15]为
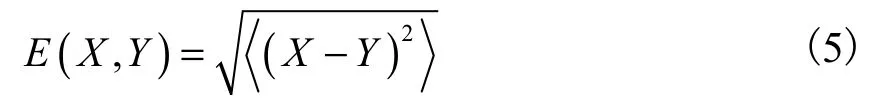
根据被评价图像与标准参考图像的逼真程度,可以得出系统参数a和b的选择规律.以含有高斯噪声的 lena灰度图为例,讨论相似系数 C ( X , Y)和偏离系数 E ( X , Y)随系统参数a和b的变化规律,并选择最优的a和b使图像的双稳响应达到最佳,进而得到最佳的二维 SR图像.分析中取计算步长 h = 1 /fsr=0.1,标准lena灰度图中添加均值为0、方差为0.4的高斯白噪声.
图6为相似系数C随参数a和b的变化规律.相似系数越大,二维 SR图像与标准参考图像的逼真度就越大,二维双稳SR的图像处理效果就越好.
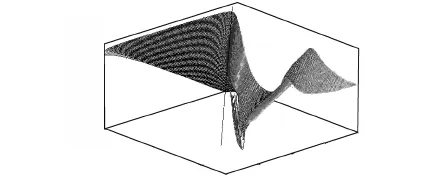
图6 h=0.1时相关系数C随参数a和b的变化规律Fig.6 Law of similarity correlation changing with regards to difference of a and b with h=0.1
在图6中,当相似系数取得可行值(能够使二维SR取得较好效果的相似系数值)时,在a、b参数平面投影的区域可以确定 a、b取值范围,这个区域大致是直线L在a、b参数平面投影与a、b参数轴所围成的平面.在这个区域内取值,二维图像的 SR都可以得到较好的效果.例如当任意取 a=7,b=1,相似系数C=0.926 5时,图像的二维SR结果如图7所示.

图7 相似系数C=0.926 5时的SR 图像Fig.7 SR image with similarity coefficient C=0.926 5
图8 为偏离系数E随参数a和b的变化规律.偏离系数越小,二维 SR图像与标准参考图像的偏离程度就越小,二维双稳SR的图像处理效果就越好.
在图8中,当偏离系数取得可行值(能够使二维SR取得较好效果的偏离系数值)时,在a、b参数平面投影的区域可以确定 a、b取值范围,这个区域大致是直线L在a、b参数平面投影与a、b参数轴所围成的平面.在这个区域内取值,二维 SR可以得到较好的图像处理效果.例如当任意取 a=4,b=100,偏离系数E=0.223 5时,图像的二维SR结果如图9所示.
由图6和图8可以看出,在相同的SR计算步长下,对于含有相同噪声强度的图像,相似系数和偏离系数这两种图像评价标准对图像的评价具有相同的效用,图 6中相似系数 C取得较大值的可行区域与图8中偏离系数E取得较小值的可行区域几乎是相对应的,都在直线 L的左方区域.在它们相对应的区域内取值,二维SR的图像都能取得较好的效果,如图7和图9所示.因此,对于含噪图像可以通过调节双稳系统参数a和b得到最佳的二维SR响应图像.
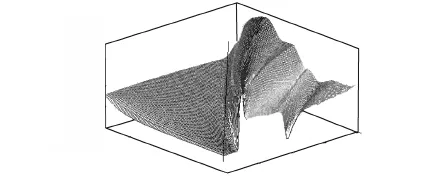
图8 h=0.1时偏离系数E随参数a和b的变化规律Fig.8 Law of deviation correlation changing with regards to difference of a and b with h=0.1

图9 偏离系数E=0.223 5时的SR图像Fig.9 SR image with departure coefficient E=0.223 5
3.2 SR步长对二维SR图像的影响
根据变尺度 SR方法,可以对计算步长进行缩放,选择合适的步长,以达到图像 SR的最优输出质量.任意选择步长 h分别为 0.05、0.1和 0.2,即压缩采样频率 fsr分别为 20、10和 5,观察不同步长 h条件下相似系数C和偏离系数E随系统参数a、b的变化规律.由于相似系数 C和偏离系数 E具有相似的变化规律,在这里只给出不同步长下相似系数 C随a、b的变化规律,且图像添加均值为0、方差为0.4的高斯白噪声.
图10和图11分别是h=0.05和h=0.2时相似系数C随a、b的变化规律.由图10、图7和图11比较可知,随着步长h的增加,相似系数 C取得可行值的范围变小,并且逼真度也随着步长的增加而降低.这表明,选择较小的步长,可以使参数 a、b有更大的选择范围,二维SR图像的输出质量可以提高.
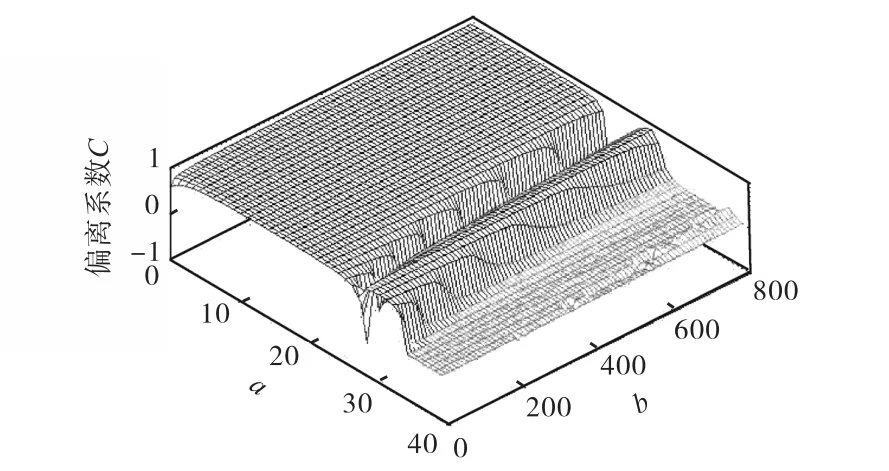
图10 h=0.05时相关系数C随参数a和b的变化规律Fig.10 Law of similarity correlation changing with regards to difference of a and b with h=0.05
图11 h=0.2时相关系数C随参数a和b的变化规律Fig.11 Law of similarity correlation changing with regards to difference of a and b with h=0.2
4 结 语
由双稳系统特性出发,提出了含噪图像的二维SR处理方法,该方法可有效降低图像中的噪声量,提高图像质量.为评价二维 SR图像的处理效果,采用相似系数和偏离系数指标来对图像质量进行客观评价,得出了双稳系统参数a和b以及变尺度SR步长h对二维SR图像的影响规律,从而确定了系统参数a、b和步长h的选择方式,为实现参数的最优化与自适应参数调节的 SR图像处理奠定了可行的研究基础.
[1] Benzi R,Sutera A,Vulpiana A. The mechanism of stochastic resonance[J]. J phys A,1981,14(11):L453-L457.
[2] 冷永刚,王太勇. 二次采样用于随机共振从强噪声中提取弱信号的数值研究[J]. 物理学报,2003,52(10):2432-2437.Leng Yonggang,Wang Taiyong. Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise[J]. Acta Physica Sinica,2003,52(10):2432-2437(in Chinese).
[3] 冷永刚,王太勇,李瑞欣. 视觉信息的随机共振[J].天津大学学报,2004,37(6):480-484.Leng Yonggang,Wang Taiyong,Li Ruixin. Stochastic resonance of visual information[J]. Journal of Tianjin University,2004,37(6):480-484(in Chinese).
[4] Ye Qinghua,Huang Haining,Zhang Chunhua. Image enhancement using stochastic resonance[C]// Proceedings of International Conference on Image Processing.Singapore,2004:263-266.
[5] MarksⅡRobert J,Thompson Benjamin,EI-Sharkawi,Mohamed A,et al. Stochastic resonance of a threshold detector:Image visualization and explanation[C]//Processings of IEEE International Symposium on Circuits and Systems. Scottsdale,Arizona,USA,2002:521-523.
[6] 张 莹,王太勇,冷永刚. 调参双稳系统图像增强应用初探[J]. 振动与冲击,2008,27(增):325-327.Zhang Ying,Wang Taiyong,Leng Yonggang. Applica tion reasrech on bistable system with tuned parameters in image enhancement[J]. Journal of Vibracation and Shock,2008,27(Suppl):325-327(in Chinese).
[7] Simonotto Enrico,Riani Massimo,Seife Charles,et al. Visual perception of stochastic resonance[J]. Phys Rev Lett,1997,78(6):1186-1189.
[8] Piana M,Canfora M,Riani M. Role of noise in image processing by the human perception system[J]. Phys Rev E,2000,68(1):1104-1109.
[9] Leng Yonggang,Wang Taiyong,Guo Yan,et al. Study of the property of the parameters of bistable stochastic resonance[J]. Acta Physica Sinica,2007,56(1):30-35.
[10] McNamara B,Wiesenfeld K,Roy R. Observation of stochastic resonance in a ring laser[J]. Phys Rev Lett,1988,60(25):2626-2629.
[11] Dykman M I,Luchinsky D G,Mannella R,et al. Stochastic resonance:Linear response theory and giant nonlinearity[J]. J Sat Phys,1993,70(1/2):463-479.
[12] Leng Yonggang,Wang Taiyong,Guo Yan,et al. Engineering signal processing based on bistable stochastic resonance[J]. Mechanical Systems and Signal Processing,2007,21(1):138-150.
[13] Leng Yonggang,Leng Yongsheng,Wang Taiyong.Numerical analysis and engineering application of large parameter stochastic resonance[J]. Journal of Sound and Vibration,2006,292(3/4/5):788-801.
[14] Collins J J,Chow Carson C,Capela Ann C,et al.Aperiodic stochastic resonance[J]. Phys Rev E,1996,54(5):5575-5584.
[15] Wang Zhou,Bovik A C. A universal image quality index[J]. IEEE Signal Process Letters,2002,9(5):81-84.

