船坞虹吸灌水廊道水力特性的数值模拟

赵 鹏，白玉川

(天津大学建筑工程学院，天津 300072)

虹吸廊道灌水是利用虹吸原理向干船坞坞室充水的一种灌水型式，廊道顶部高程大于海面最高水位，因此不需设置阀门．当开始灌水时，使用真空泵抽气产成虹吸；停止灌水时，开启设置在顶部的空气阀，虹吸作用即因空气进入而中断．与传统的闸阀灌水相比，虹吸廊道灌水具有结构简单、断流迅速、运行管理方便可靠等优点，近年来在青岛北海船舶重工、广州中船龙穴、大连船舶重工等 10余座大型修造船坞中得到广泛使用[1-3]．

修造船坞对灌水时间有着严格的控制，如修船坞灌水一般要求在 1～2.5 h内完成．由于船坞布置空间有限，虹吸灌水廊道截面、虹吸段转弯半径等的几何尺寸受到限制，在大流量灌水的情况下，廊道过流流速较大，廊道壁面可能会遭到空蚀破坏．廊道内部结构如消能工的设置则需兼顾灌水流量和在工程设计中流速、压强等参数在灌水廊道三维分布的准确获取，有助于优化廊道体型，可在保证廊道壁面不受到空蚀破坏的前提下，增大灌水流量，减少灌水时间，提高船坞工作效率，数值模拟方法正在此显示出其优越性．因此本文结合某修船坞虹吸灌水廊道水力模型试验，对其水力特性进行了数值模拟研究．

1 数学模型及求解

1.1 控制方程

根据 Reynolds应力处理方式的不同，湍流模型可分为 Reynolds应力模型和涡黏模型．涡黏模型根据确定涡黏系数tμ需求解微分方程的数目，分为零方程模型、一方程模型和两方程模型等．目前使用较多的是两方程模型中的 k-ε模型及其改进型，笔者使用k-ε模型封闭时均N-S方程．

连续方程

式中：ui为 xi方向的时均速度分量，i＝1，2，3；p为流体时均压力；μ 为流体的动力黏度；μt为涡黏系数，方程中通用模型常数取值分别为[4]：Gk为由于平均速度梯度引起的湍动能k的产生项．

1.2 网格划分及方程求解

完整的船坞灌水廊道数值模拟计算域应该包括进水口、灌水廊道和坞室3个部分．但是考虑进水口和坞室流态将耗费大量计算机硬件资源，另外本文研究的是灌水初始时刻的廊道水力特性，此时可近似认为坞室没有海水流入，因此只将灌水廊道作为计算域．

灌水廊道结构如图 1所示，廊道进口尺寸为4.20,m×2.80,m．廊道出口设在高程－8.30,m 的坞室底部，尺寸为 10,m×10,m．由于灌水廊道结构复杂，为提高网格划分质量和效率，使用结构网格和非结构网格结合的方法对计算域进行划分．在进口段和虹吸段等具有规则形状的区域使用结构网格，在消能段等结构较为复杂的区域使用非结构网格．生成的网格数约为142×104，节点数约为152×104．

图1 船坞虹吸灌水廊道结构示意Fig.1 Schematic diagram of siphon passage of dockyard

使用有限体积法对控制方程组进行离散，采用二阶迎风格式，压力和速度的耦合使用 SIMPLER算法[5]．进口边界给定灌水流量，湍流动能 kin和耗散率εin由下列公式计算：其中inu为廊道进口流速；D为当量直径．出口设为压力出口边界，给定大气压值．在廊道壁面上采用无滑移条件，壁面上法向速度及其导数为零，近壁区使用壁函数法处理．数值计算使用非恒定流模型，时间步长取 0.002,s，以廊道进出口流量近似相等和驼峰断面特征点压强基本稳定为收敛判别标准[6]．

2 计算结果分析

2.1 流场分析

数值计算取 6个工况水位，分别为 0.53,m、1.50,m、2.20,m、2.92,m、3.24,m 和 4.20,m，对应的灌水流量取值范围为34.5～41.5,m3/s，其中2.20,m为设计进出坞水位．文中主要对设计水位下灌水廊道的流场特性进行分析．

通过数值计算，得到了虹吸灌水廊道流速、压强、湍流动能和湍流耗散率的分布．图2和图3为廊道断面的速度矢量分布，图4为灌水廊道水平面的速度等值线分布，各面的高程由上向下为：-4.75,m、-5.90,m、-7.05,m、-8.2,m、-9.40,m 和-10.60,m(廊道底板高程为－10.80,m)．在图2中灌水水流自虹吸下行段流出后冲击廊道底板，形成一个水垫后分向两侧，受到底板和边墙的限制形成两个水平轴向的漩涡．由于水垫的顶托作用，使水流不能直接冲击廊道底板，减轻了底板的冲刷．结合图 4也可以看出，-10.60,m水平面处于下行段出口下方的位置流速较小，两侧由于漩涡与底板相切而形成高速区．漩涡向后发展依次撞击消能立柱底部和隔墙后形成回流，与来流掺混后向上通过隔墙．从图 3可以看出，隔墙立柱间隙较小，水流以较大速度向后喷射，并在隔墙立柱后形成漩涡．最后水流同消能段后墙碰撞后急剧转向进入廊道出口段，如图 4所示，在出口段底部流速集中在4～5,m/s．图2和图3所示的流速矢量分布与模型廊道掺气形成的气泡反映的实际流动是一致的，表明数值模拟较好地反映了灌水廊道流场分布．

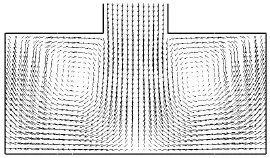
图2 下行段下方纵断面速度矢量分布Fig.2 Velocity vector distribution of profile beneath descending section

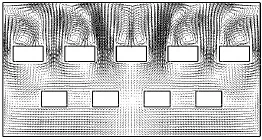
图3 消能段顶部平面速度矢量分布Fig.3 Velocity vector distribution of roof plane in dissipation section

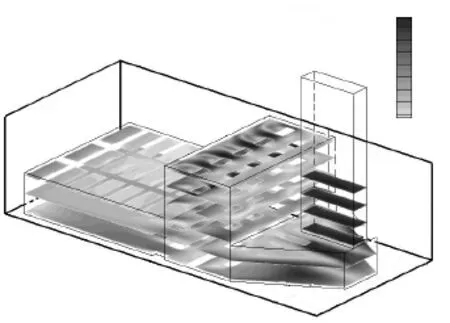
图4 灌水廊道水平面速度等值线分布Fig.4 Iso-velocity contours of horizontal plane in siphon passage

图5 ～图8分别为灌水廊道顶部和底部水平面的湍流动能k与湍流耗散率ε分布，其高程为-5.90,m和-9.40,m．结合图4可以看出，消能段顶部水流在隔墙立柱后形成漩涡并与壁面相撞，水流紊动较为强烈．因此对比两平面的湍流参数分布，湍流动能 k和湍流耗散率 ε在－5.90,m平面明显大于－9.40,m平面，其中湍流耗散率 ε在消能段后墙处达到峰值，表明灌水水流能量主要在此处被消刹[7]．

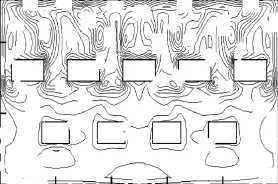
图5 －5.90 m湍流动能等值线(单位：m2/s2)Fig.5 Contours of turbulent kinetic energy on -5.90 m level(unit：m2/s2)

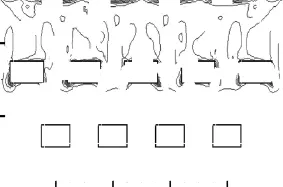
图6 －5.90,m湍流耗散率等值线(单位：m2/s2)Fig.6 Contours of turbulent dissipation rate on －5.90,m level(unit：m2/s3)

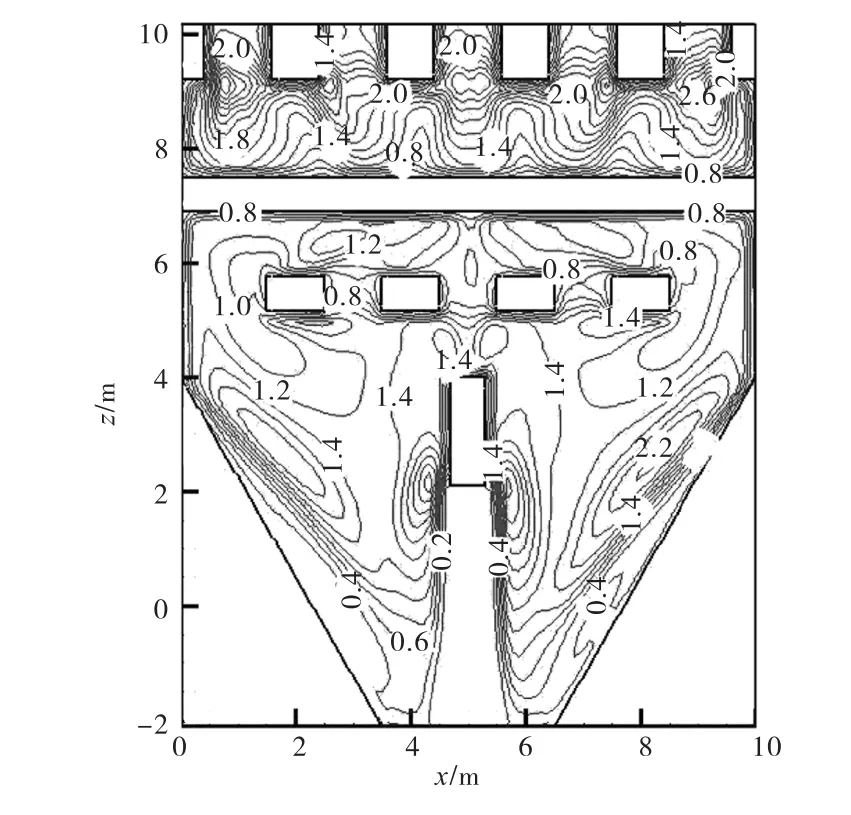
图7 －9.40,m湍流动能等值线(单位：m2/s2)Fig.7 Contours of turbulent kinetic energy on －9.40,m level(unit：m2/s2)

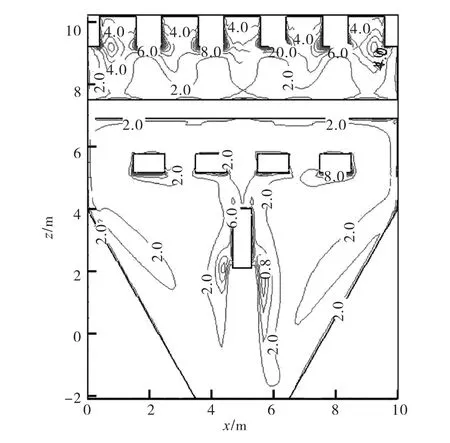
图8 －9.40,m湍流耗散率等值线(单位：m2/s2)Fig.8 Contours of turbulent dissipation rate on －9.40,m level(unit：m2/s3)

2.2 驼峰压强计算结果与试验结果的对比

由于虹吸灌水廊道驼峰高于水面，并且廊道虹吸段的转弯半径较小，驼峰底部压强受到水流离心力作用降低，一般认为驼峰底部是灌水廊道中最易发生空化的位置．为了避免廊道壁面遭受空蚀破坏，需要进行模型试验以确定驼峰压强是否满足规范要求．

虹吸灌水廊道模型试验按重力和阻力相似准则设计，采用正态水力模型，几何比尺λL＝16．为达到糙率相似，模型廊道使用有机玻璃制作，糙率为0.008,0～0.008,3，换算为原型与混凝土护面糙率相差很小[8]．沿程布置 8个测点，压强采用测压管以水柱高度方式测量，灌水流量通过设置在模型坞室出水口的矩形量水堰测得．试验分为 7个工况，水位取值范围为0.06～4.20,m．

图9为不同水位廊道驼峰顶部和底部的压强计算值与模型试验值的对比，压强计算值与水位基本呈线性关系．与试验值相比，在低水位时峰顶压强计算值较试验值偏大，原因可能是试验中水流未完全进入阻力平方区造成的，另外数值模拟中未考虑进水口流态也会对计算结果产生影响．峰底压强计算值则基本与试验值一致，在灌水廊道最易发生空化现象的设计低水位0.53,m，驼峰底压强计算值为2.70×104Pa，与模型试验值偏差小于 0.05×104Pa．总的来说，驼峰压强计算值与试验值吻合较好．

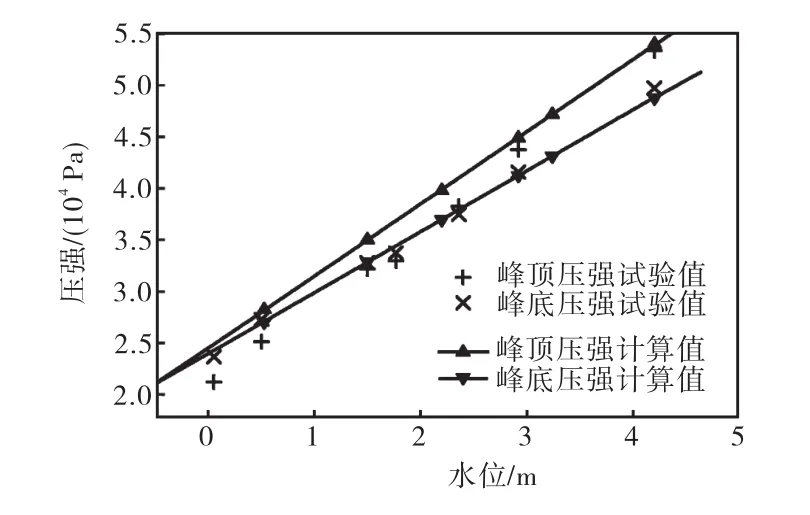
图9 廊道驼峰压强计算值Fig.9 Calculated pressure of passage hump

2.3 驼峰断面压强分布分析

通过数值计算得出驼峰断面压强分布见图 10～图 13．灌水廊道虹吸段的水流主要受重力和离心力作用．重力作用使驼峰底部压强大于顶部压强，并且使驼峰断面压强随着外海水位的上升而增大．离心力作用方向沿驼峰半径向外，因此驼峰顶部受水流离心力作用压强增大，相反离心力在驼峰底部起减小压强的作用．在高水位时廊道水流流速较大，离心力作用则更加明显，从图 10～图 13中可以看出，峰顶与峰底的压差值随着水位的升高逐渐增大，压差值由0.05×104Pa升高到 0.52×104Pa，同时离心力作用也使得各水位下灌水廊道驼峰底部压强均小于顶部压强．而在0.53,m 和1.50,m 水位，廊道流速偏低，离心力作用相对较小，不足以改变重力作用下驼峰底部压强大于顶部压强的分布，因此驼峰断面压强出现了如图10和图11所示的中间大、上下小的分布．

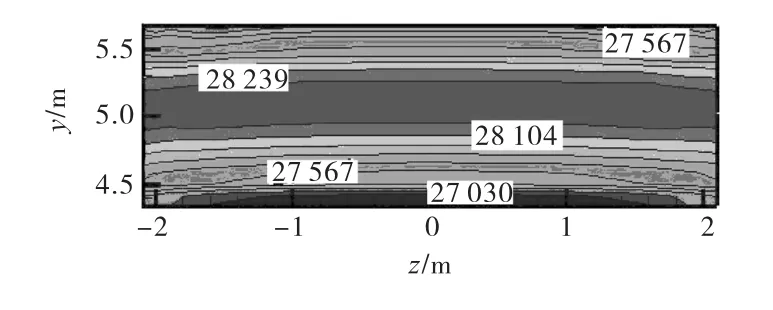
图10 0.53 m水位压强分布(单位：Pa)Fig.10 Distribution of pressure on 0.53 m level(unit：Pa)

图11 1.50,m水位压强分布(单位：Pa)Fig.11 Distribution of pressure on 1.50,m level(unit：Pa)

图12 2.20,m水位压强分布(单位：Pa)Fig.12 Distribution of pressure on 2.20,m level(unit：Pa)

图13 3.24,m水位压强分布(单位：Pa)Fig.13 Distribution of pressure on 3.24,m level(unit：Pa)

在图10中灌水廊道设计低水位0.53,m运行时，驼峰负压可满足规范中68.6～78.4,kPa的允许值[9]．但是设计合理的虹吸灌水廊道运行时，应使驼峰断面压强的分布趋于均匀[10]．从图 12可以看出，此船坞灌水廊道在进出坞水位 2.20,m运行时，峰顶与峰底的压差值较大，约为 0.34×104,Pa．灌水廊道设计应进一步优化以减小驼峰断面压差，可适当增大虹吸段转弯半径，以减小水流离心力作用．

3 结 论

(1)灌水水流的动能主要通过在隔墙立柱后射流与壁面相撞来消刹，消能立柱和隔墙的消能作用相对较小．

(2)灌水廊道在低水位运行时，驼峰断面压强会出现中间大、上下小的分布，此时驼峰顶部和底部有可能同时发生空化，应引起足够重视．

(3)此虹吸灌水廊道在进出坞水位运行时，驼峰断面压差值较大，虹吸段半径可做进一步调整，以减小离心力影响，放宽流速限制．

［1］ 白玉川，张效先. 山海关船厂 15万吨级修船坞虹吸灌水水力模型试验研究[J]. 船舶力学，2003，7(4)：36-49.Bai Yuchuan，Zhang Xiaoxian. Hydraulic modeling studies for filling water by a new type of siphon passage in the 15 ten-thousand-ton class lay-up dock of Shanhaiguan dockyard[J]. Journal of Ship Mechanics，2003，7(4)：36-49(in Chinese).

［2］ 张效先，杨建华，白玉川. 修、造船坞虹吸灌水流道的设计方法[J]. 天津大学学报，2006，39(2)：204-208.Zhang Xiaoxian，Yang Jianhua，Bai Yuchuan. Design of the siphon piping of the ship repairing-building dock[J]. Journal of Tianjin University，2006，39(2)：204-208(in Chinese).

［3］ 赵 鹏．船坞虹吸灌水廊道水力特性的数值模拟研究[D]. 天津：天津大学建筑工程学院，2009.Zhao Peng． Numerical Simulation on Hydraulic Characteristics in Siphon Passage of Dockyard[D]. Tianjin：School of Civil Engineering，Tianjin University，2009(in Chinese).

［4］ Shiono K，Scott C F，Kearney D. Predictions of solute transport in a compound channel using turbulence models[J]. Journal of Hydraulic Research，2003，41(3)：247-258.

［5］ Ferziger J H，Peric M. Computational Methods for Fluid Dynamics[M]. Berlin：Springer，2002.

［6］ 王晓玲，段琦琦，佟大威，等. 长距离无压引水隧洞水气两相流数值模拟[J]. 水利学报，2009，40(5)：596-602.Wang Xiaoling，Duan Qiqi，Tong Dawei，et al. Numerical simulation of water-air two-phase flow with free surface in long tunnel[J]. Journal of Hydraulic Engineering，2009，40(5)：596-602(in Chinese).

［7］ 付 波，牛争鸣，李国栋，等. 竖井进流水平旋转内消能泄洪洞水力特性的数值模拟[J]. 水动力学研究与进展：A辑，2009，24(2)：164-171.Fu Bo，Niu Zhengming，Li Guodong，et al. Numerical simulation of level swirling flow of inner energy dissipation discharge tunnel with shaft inlet[J]，Journal of Hydrodynamics：Ser A，2009，24(2)：164-171(in Chinese).

［8］ 贺昌林，余 挺，张建民，等. 长泄洪洞模型糙率修正方法研究[J]. 四川大学学报：工程科学版，2007，39(6)：26-29.He Changlin，Yu Ting，Zhang Jianmin，et al. Revision of roughness on the wall of a long tunnel in physical model[J]. Journal of Sichuan University：Engineering Science Edition，2007，39(6)：26-29(in Chinese).

［9］ 中华人民共和国交通部. JTJ 253—87 干船坞坞门及灌水排水系统设计规范[S]. 北京：人民交通出版社，1987.Ministry of Transport of the People's Republic of China.JTJ 253—87 Standard for Design of Dock Gates and Ffilling and Emptying Systems of Dry Docks[S].Beijing：China Communications Press，1987(in Chinese).

［10］ 习和忠，王常生，陈秀玉. 虹吸式输水管道驼峰断面上压强分布的计算[J]. 水运工程，1987，12(7)：8-12.Xi Hezhong，Wang Changsheng，Chen Xiuyu. Pressure calculation of hump section in siphon passage[J]. Port and Waterway Engineering，1987，12(7)：8-12(in Chinese).