钢管混凝土收缩徐变模型及计算方法对比分析

王玉银，耿 悦,2，张素梅

(1. 哈尔滨工业大学土木工程学院，哈尔滨 150090；2. 悉尼大学土木工程学院，悉尼 2006)

为了准确预测混凝土结构长期静力响应，各国学者通过对大量试验数据进行拟合，提出了多种混凝土收缩徐变预测模型，如：欧洲规范中提供的 EC2模型，美国混凝土协会 209委员会提出的 ACI 209(1992)模型，法国的AFREM模型，欧洲混凝土委员会——国际预应力混凝土协会提出的MC90模型，美国Bazant等提出的B3模型等．文献[1]对各模型的相关规定及适用范围进行了具体介绍．

对于钢管混凝土而言，核心混凝土处于密闭环境中，其收缩徐变量远小于外露在大气中的混凝土，但研究发现时效作用仍对钢管混凝土的静力性能有较大影响，在结构设计中应予以考虑[2-3]．但是，目前各国规范规程中尚未提出针对钢管混凝土构件的收缩徐变模型．广大学者及设计人员在进行钢管混凝土长期静力性能分析时，均借用混凝土的收缩徐变模型进行分析，不同模型计算所得结果相差较大[4]．

本文结合钢管混凝土的收缩徐变机理，对 EC2模型、ACI 209(1992)模型、AFREM 模型、MC 90模型及 B3模型进行修正，同时采用逐步积分法，推导出钢管混凝土构件时效分析的计算公式，进行钢管混凝土构件长期变形分析．采用收集到的 77个钢管混凝土短柱的长期变形试验结果对 5种修正后的混凝土收缩徐变模型的预测精度进行比较，确定适用于预测钢管混凝土长期静力响应的模型．选用该模型，对比分析有效模量法、平均应力法、龄期调整的有效模量法这 3种简化计算方法在分析钢管混凝土构件长期静力性能时的精度，为结构设计提供参考．

1 钢管混凝土收缩徐变模型确定

1.1 混凝土收缩徐变模型的修正

普通外露素混凝土的收缩由自然收缩及干燥收缩 2部分构成，徐变包括基本徐变与干燥徐变．对于钢管混凝土构件，由于钢管的密闭作用，核心混凝土在密闭环境下不与外界发生水分交换，仅发生自然收缩与基本徐变，其收缩徐变量不受构件尺寸与环境相对湿度的影响．该特点与大体积混凝土的收缩徐变特性极为相似．ACI 209(1992)模型采用同一公式计算密闭混凝土与大体积混凝土的收缩徐变．因此对于未区分自然收缩与干燥收缩或(和)未区分基本徐变与干燥徐变的模型，可根据混凝土体积无穷大的假设对模型进行修正，即将核心混凝土名义厚度 h(h＝2Ac/u，其中 Ac为核心混凝土面积，u为构件周长)设为无穷大，代入相应模型公式进行计算．

具体而言，考虑徐变时，对于 AFREM 与 B3模型，采用基本徐变公式进行计算；对于 ACI模型，选取针对密闭混凝土与大体积混凝土提出的徐变公式进行计算，设h＝∞；对于EC2与MC90模型，由于公式中未区分基本徐变与干燥徐变，计算时设 h＝∞．在考虑核心混凝土收缩时，对于 EC2与 AFREM模型，直接采用自然收缩公式进行计算；对于 MC90与 B3模型，将核心混凝土名义厚度 h设为无穷大后，计算所得收缩值为 0；对于 ACI模型，设收缩量为 0．可见，在采用修正后的 MC90、ACI与 B3模型分析钢管混凝土长期静力性能时均不能考虑收缩的影响，对于自然收缩量较大的钢管高强混凝土，这3种模型可能将不再适用．此外，AFREM模型未提供混凝土弹性模量计算公式，采用该模型进行分析时，参考了MC90模型中的相关规定计算混凝土弹性变形．

1.2 钢管混凝土构件时效分析理论

混凝土收缩徐变模型用于描述恒定应力下混凝土的时效特性．钢管混凝土构件在持荷作用下，时效效应会引起核心混凝土所承担的荷载随时间发展不断降低，即所谓的应力重分布现象．核心混凝土在变荷载作用下的时效效应的积分公式[5]可表示为

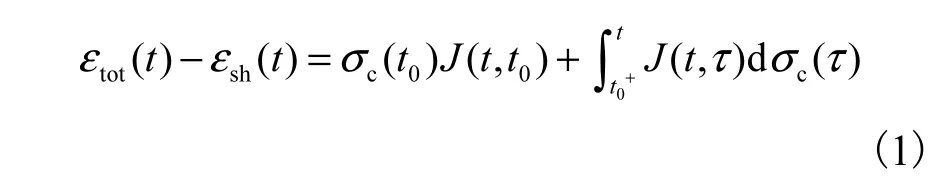
式中：εtot(t)为 t时刻混凝土总应变量(弹性变形＋徐变变形＋收缩变形)；εsh(t)为混凝土的收缩变形量(其余与荷载无关的应变量，如温度应变等也可用相同形式表示)；t0为混凝土的加载龄期；σc(t)为 t时刻的混凝土应力；J(t，τ )为徐变函数，表示τ 时刻施加于混凝土上的单位应力在 t时刻所引起的长期变形．其中εsh(t)与 J(t，τ )可由相应的混凝土收缩徐变模型计算得到．

式(1)可通过逐步积分法得到近似解．逐步积分法是利用梯形积分法则，通过k＋1个时间点将时间t离散为 t0，t1，t2，…，ti，…，tk，共 k 个小时间段，则式(1)的计算结果可以近似为

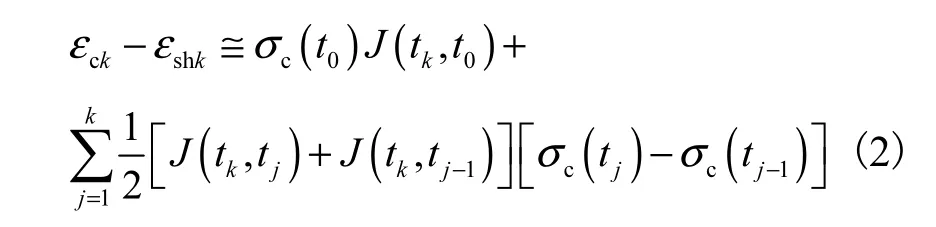
式中：σc(tj)(下文中简写为σcj)为 tj时刻混凝土所受应力；εck为构件在 tk时刻的总变形(包括弹性变形、徐变变形及收缩变形)；εshk为核心混凝土在tk时刻的收缩变形；J(tk，tj)为徐变函数，其物理意义为 tj时刻作用于构件上的单位应力持荷至 tk时刻所引起的变形．

在时效分析中，认为钢材为线弹性材料，其弹性模量用Es表示．若管中尚埋有钢筋，则钢筋总层数为nr，每层钢筋总面积、弹性模量及距参考轴距离分别用 Ar(a)、Er(a)及 yr(a)表示，其中 a＝1，…，nr．

考虑混凝土时效作用后，钢管混凝土构件所受截面内力可表示为

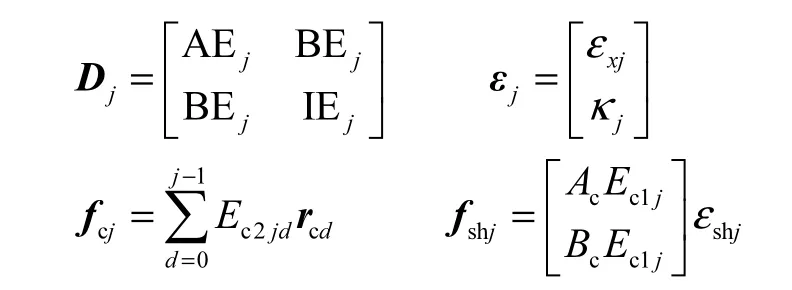
式中：rij为tj时刻构件内力的行列式；εj为构件截面在 tj时刻参考轴上应变(εxj)及截面斜率(κj)这2个基本未知量组成的行列式；fcj为 tj时刻徐变影响向量；fshj为 tj时刻收缩影响向量；Ac为构件截面混凝土部分的面积；Bc为构件截面混凝土部分的面积矩．

rcd为 td时刻构件混凝土部分所受内力，包括轴向内力(Ncd)及弯矩(Mcd)

表1 构件几何及材料参数Tab.1 Geometrical and material properties of selected test specimens

式中cI为构件截面混凝土部分惯性矩．

根据力的平衡条件即可算得tj时刻构件应变εj

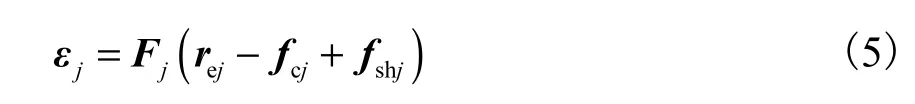
式中Fj为Dj的逆矩阵，即

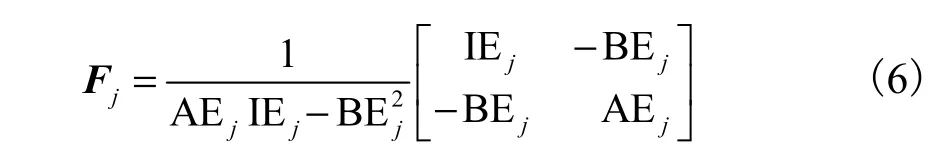
得到构件截面应变分布后，tj时刻构件截面应力分布通过应力应变关系确定为

1.3 混凝土收缩徐变模型比较分析

本文收集了文献[2，3，6-15]共 77个钢管混凝土短柱的试验结果，采用逐步积分法，比较分析修正后的 EC2、MC90、AFREM、B3及 ACI模型在预测钢管混凝土构件长期静力性能时的精度．构件参数范围较广，包括圆形、方形、矩形钢管混凝土轴压及偏压短柱，混凝土强度 15～60 MPa，含钢率 0.02～0.20，持荷时荷载轴压比0.1～0.8，加载龄期7～180 d．

1.3.1 长期变形随时间变化曲线对比结果

钢管混凝土构件的长期变形随时间变化规律有长期总变形曲线与长期变形增量曲线 2种表示方式．本文根据各文献所选取的不同表示方式，分别对构件变形增量(εin)与变形总量(ε)随时间(t)变化规律进行分析．各典型构件具体参数见表1．

在各构件长期变形分析中，当缺乏试验值时假设钢管弹性模量 Es＝2.0×105MPa，混凝土弹性模量根据混凝土 28 d抗压强度(fcm28)实测结果由相应的模型公式计算得到．由于使用 B3模型时需要混凝土配比信息，对于未提供该信息的试验构件，仅采用了其余4种模型进行分析．

图1所示为加载龄期为28 d的圆形、方形、普通钢管混凝土构件在轴向及偏心荷载作用下的长期变形曲线以及相应的5种模型的分析结果．偏心荷载作用下的构件曲线为钢管外表面最大压应力边缘的变形结果．图1中，D为圆钢管混凝土构件直径，B为方钢管混凝土构件边长或矩形构件短边边长．由图1可以发现，B3模型略微高估了构件长期变形，ACI模型的预测结果则比试验结果偏低，其余3种修正后模型的预测结果与试验数据均吻合较好．

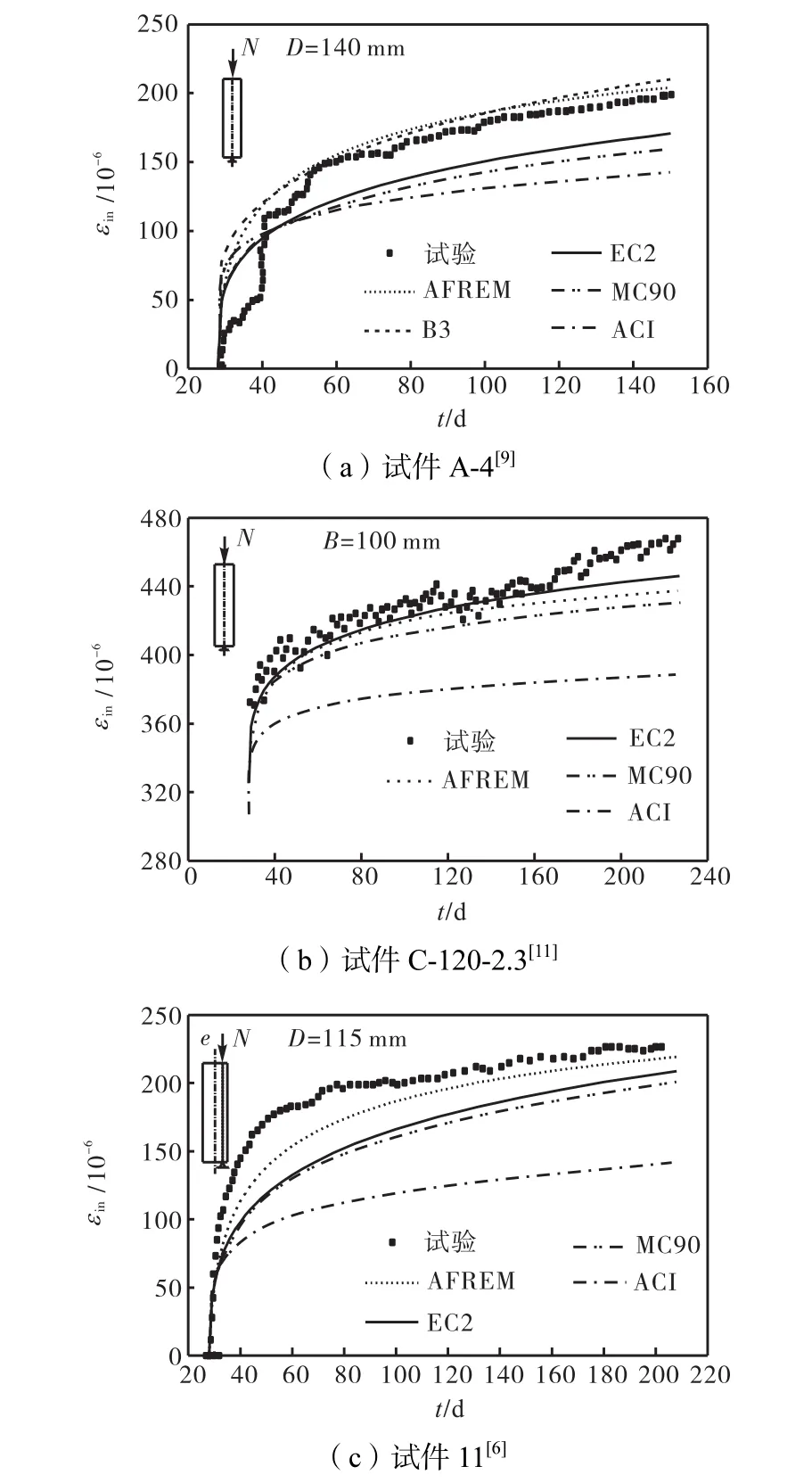
图1 普通钢管混凝土短柱28 d加载长期变形计算与试验结果比较Fig.1 Comparisons of calculated and measured long-term deformations for normal CFST columns loaded at 28 days

图2所示为晚龄期加载的钢管混凝土轴压及偏压构件的长期变形曲线与相应的各模型预测结果．图2中2个试件的加载龄期均在 180,d以上．比较各曲线发现，AFREM 模型会高估晚龄期加载的钢管混凝土构件的长期变形，ACI模型的计算结果仍比试验结果偏低．

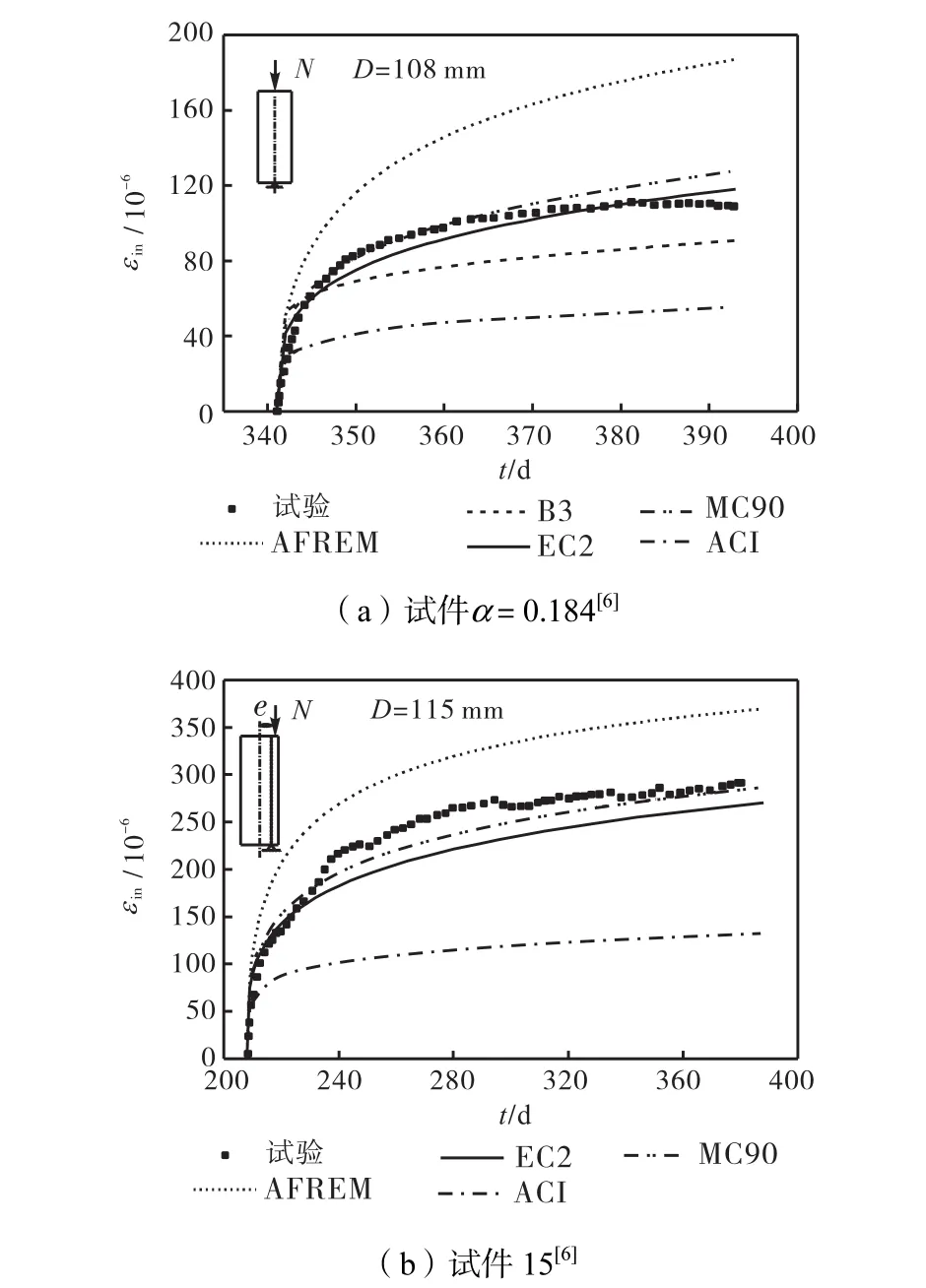
图2 普通钢管混凝土短柱晚龄期加载长期变形计算与试验结果比较Fig.2 Comparisons of calculated and measured long-term deformations for normal CFST columns loaded at t0≥180 days

图3所示为各种修正后模型在预测钢管微膨胀混凝土构件长期变形时的典型比较结果．其中，图3(a)中试验构件的膨胀剂掺量为水泥质量的 12%，图3(b)中构件的膨胀剂掺量为水泥质量的 20%，基本涵盖了钢管混凝土实际结构中普遍采用的膨胀剂掺量范围．观察图 3可以看出，修正后的 MC90模型、EC2模型、AFREM模型可以较精确地预测28 d加载的钢管微膨胀混凝土构件的长期静力性能．

1.3.2 各模型预测精度的统计结果在实际工程中，设计施工人员更加关心的是结构构件的收缩徐变终值．为了全面评价各模型在预测钢管混凝土构件长期静力性能时的精确性与可靠性，将所有构件在试验结束时长期变形增量的计算结果与实测结果进行对比分析．

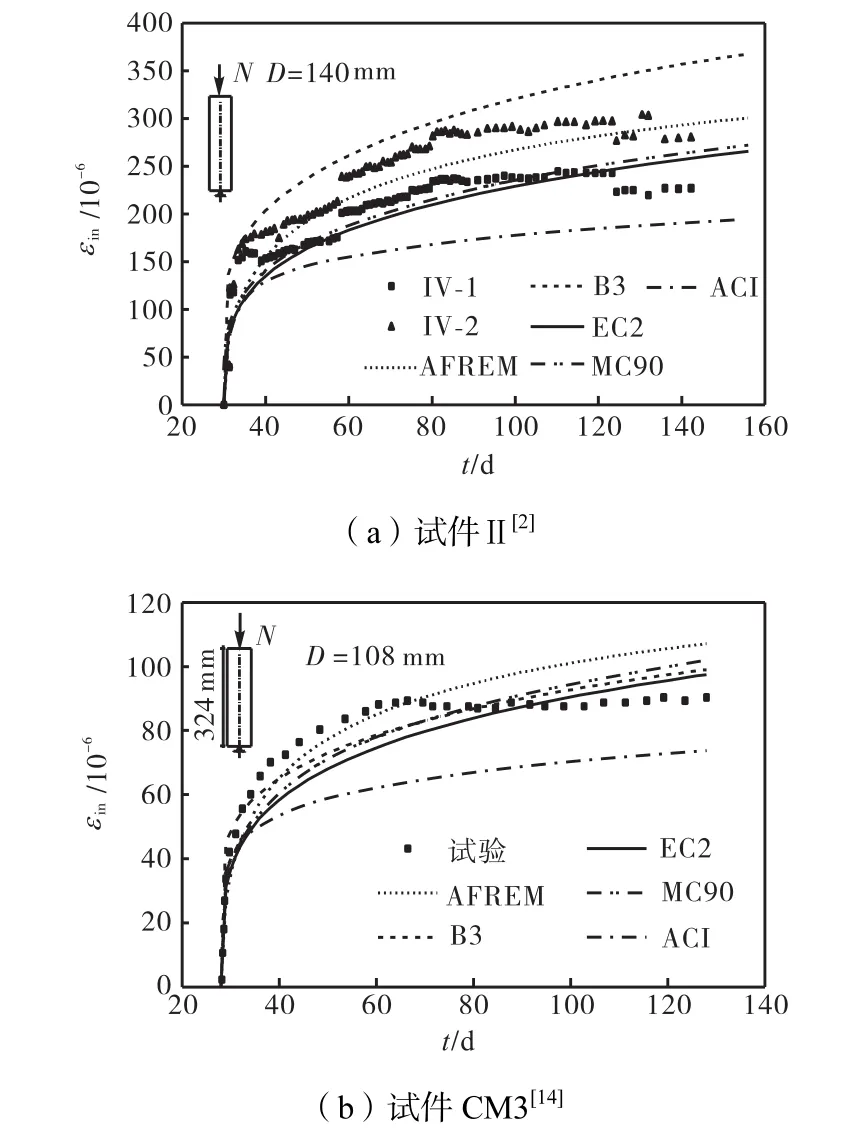
图3 钢管微膨胀混凝土长期变形计算与试验结果比较Fig.3 Comparisons of calculated and measured long-term deformations for CFST columns with expansive additive

图4 构件长期变形增量比较Fig.4 Comparisons between long-term incremental deformations of specimens

图4统计了所有钢管混凝土构件在其长期试验结束时的长期变形增量的实测结果与各修正后混凝土收缩徐变模型的分析结果之间的差异．图中εm为测得的钢管混凝土构件长期变形增量，εc为相应的模型计算结果．将图中散点进行线性回归，回归线截距设为零，回归线方程与相关系数如图4所示．图4(c)中，AFREM 模型高估了构件长期变形，这主要是由于 AFREM 模型对晚龄期加载的钢管混凝土构件长期变形的预测结果普遍高于试验结果．从图 4(d)可以看出，修正后的 B3模型与试验数据对比结果的离散性较大．ACI模型(图 4(e))则低估了构件长期变形．修正后的MC90模型的分析结果与实测结果较为接近．但是 MC90模型不能考虑收缩的影响，不适用于钢管高强混凝土的长期静力响应预测．修正后的EC2模型可以较为全面地反映钢管混凝土的收缩徐变特性，且预测结果与试验数据吻合最好，适用于钢管混凝土长期静力响应分析．

此外，由于混凝土长期试验的离散性，对于部分钢管混凝土构件，即使采用预测精度最高的EC2模型分析所得构件长期变形与实测结果之间仍存在30%的偏差．对于文献[10-13]中同时测量了加载初期弹性变形的试件，如果进一步对比其在试验结束时的总变形分析与实测结果，可以发现两者之间的偏差显著减小，仅为10%左右(见图5)．实际工程中，设计施工人员并不刻意区分弹性变形与长期变形，更关心结构总变形的预测结果，因此采用修正后的 EC2模型分析钢管混凝土结构长期静力性能，可以得到令人满意的结果．

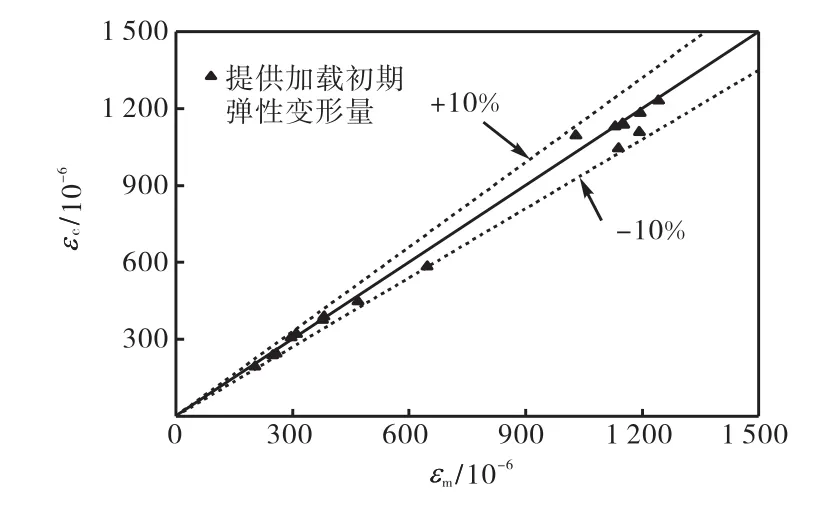
图5 构件长期试验结束时总变形比较(EC2模型)Fig.5 Comparisons between total deformations of specimens at the end of long-term tests(model EC2)

2 收缩徐变简化计算方法对比及验证

采用逐步积分法对钢管混凝土构件及结构的长期静力性能进行分析，分析精度较高．但是，在采用逐步积分法对 tk时刻混凝土构件长期变形进行预测时，需要调用前k-1步所有子步中构件截面的应力及应变计算结果方可求解，过程繁琐．有效模量法[16]、平均应力法[16]及龄期调整的有效模量法[16]均对逐步积分法的迭代部分进行了代数近似，是结构时效分析的简化方法．为方便设计施工人员在钢管混凝土实际工程中考虑混凝土时效作用的影响，本文将这3种简化计算方法的预测结果与逐步积分法的分析结果进行对比，给出了各种简化计算方法的适用范围，并提出设计建议．所选构件参数基本涵盖了钢管混凝土实际结构的设计参数范围．

为了方便比较与使用，仍沿用式(3)的形式表述采用有效模量法、平均应力法与龄期调整的有效模量法获得的混凝土时效本构，依次分别为

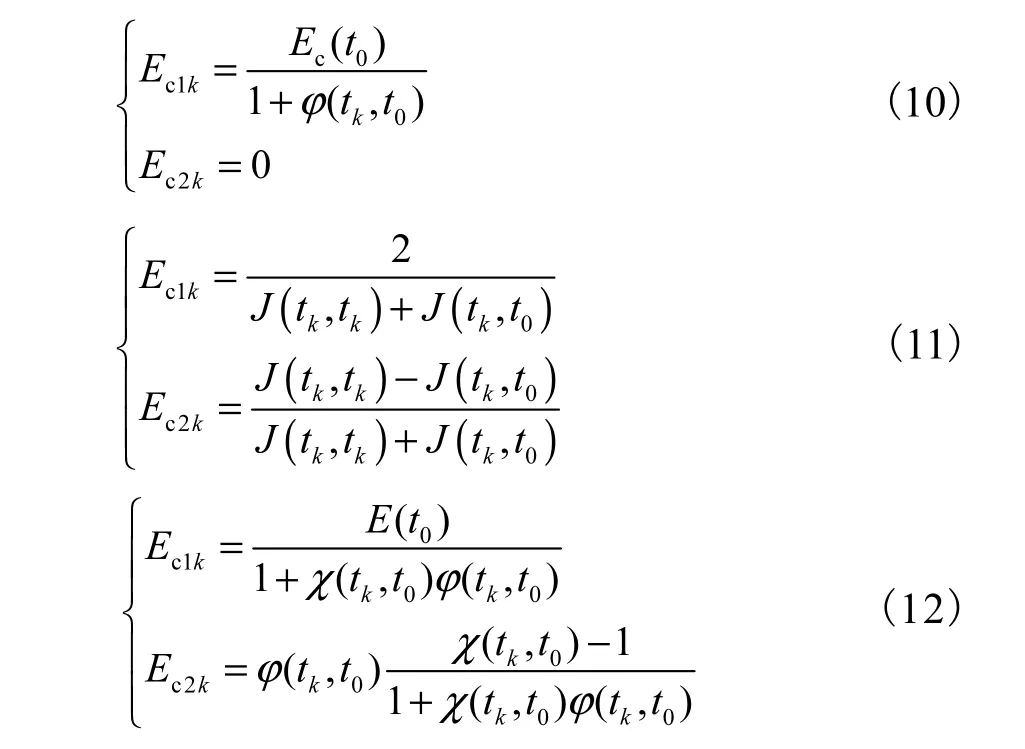
在采用各种简化方法分析钢管混凝土构件长期静力响应时，只需将式(10)～式(12)代入式(3)，采用与第1.2节相同的计算过程进行计算．其中龄期调整的有效模量法的老化系数分别采用 Bazant等[16]与Neville等[17]提出的公式进行计算，以下分别称为AAEM-Bazant法与AAEM-Neville法．将简化方法的分析结果与逐步积分法的分析结果进行对比，确定不同简化计算方法在分析钢管混凝土构件长期静力性能时的适用范围．前文统计分析结果证明，5种修正后的模型中，EC2模型最适用于预测钢管混凝土构件的时效作用，因此分析时采用该模型描述核心混凝土的收缩徐变．构件参数包括含钢率α＝0.04～0.20，核心混凝土150,mm×300,mm标准圆柱体试件28,d抗压强度平均值为 20～60,MPa(即 C25～C70混凝土)，加载龄期 3,d～3,a，钢材弹性模量 Es＝2.0×105,MPa．

图6为各简化模型与逐步积分法分析结果之间的偏差的包络图．图中横坐标为加载龄期(t0)的对数坐标，纵坐标为相应简化计算方法预测结果与逐步积分法预测结果之间的差异，以百分比的形式表示，数值为负时表示简化方法的分析结果比逐步积分法的计算结果低．分析发现，当构件含钢率在 0.04～0.2范围内变化时，各简化分析方法的计算精度随构件含钢率变化的波动幅度很小，不超过 1%．因此图中仅提供了相应混凝土强度及加载龄期下，各种含钢率的钢管混凝土构件从加载龄期到 50 a的时间段内，简化计算方法与逐步积分法计算所得结果的偏差的最大与最小值．对于龄期调整的有效模量法和有效模量法(EM 法)，最大偏差出现在持荷结束阶段．而平均应力法预测结果的最大偏差则出现在收缩徐变发展的初期阶段．

由图6可以看出，各种简化计算方法在预测钢管混凝土构件长期变形时，其计算结果与逐步积分法的预测结果之间的差异均较小，最高在 10%左右．其中，AAEM-Bazant法的分析精度最高，与逐步积分法计算结果之间的偏差在 5%以内．MS法与 AAEMNeville法的计算精度次之，它们与逐步积分法之间的最大偏差分别为 5.4%与 6.9%．有效模量法的计算精度较差，对早龄期加载的构件，其长期变形的预测结果的最大偏差约为10%．但是，有效模量法的预测精度随着构件加载龄期的增加迅速提高，当加载龄期为 28 d时，有效模量法计算结果与逐步积分法的计算结果之间的差异已在 5%以内．值得注意的是，EM法与 AAEM 法均低估了钢管混凝土构件的长期变形，而 MS法的计算结果则比逐步积分法计算结果高．综合以上分析，各分析方法的适用范围如下：从结构安全考虑，建议采用偏于保守的MS法进行结构长期静力性能分析；EM 法公式简单，计算方便，当对长期效应的预测精度要求不高时，设计人员也可考虑使用；在进行重要结构的长期静力性能分析时，仍建议采用计算精度较高的分析方法(如逐步积分法)进行分析．

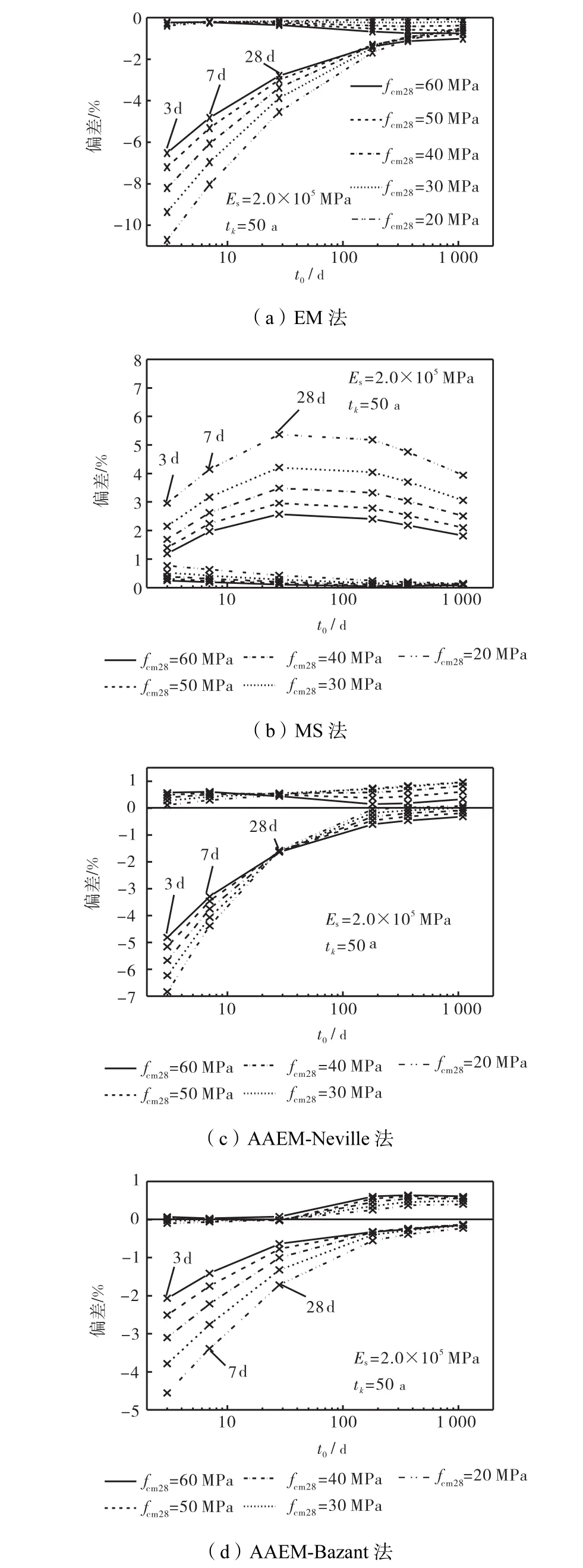
图6 简化计算方法与逐步积分法长期变形计算结果之间的偏差Fig.6 Variation between the long-term deformation calculated results using the algebraic methods and the step-by-step integration method

3 结 论

(1) ACI模型普遍低估了钢管混凝土构件长期变形，AFREM 模型对晚龄期加载的钢管混凝土构件的长期变形预测结果偏高，B3模型与 MC90模型均未考虑收缩变形的影响，因而不适用于钢管高强混凝土的长期性能预测，修正后的 5种收缩徐变模型中，EC2模型的计算结果与各试验曲线吻合最好，可以较全面地反映密闭混凝土的收缩徐变特性，适用于钢管混凝土构件的长期静力响应分析．

(2) 有效模量法、平均应力法、龄期调整的有效模量法，这3种简化的混凝土收缩徐变计算方法在预测钢管混凝土构件长期静力响应时与逐步积分法之间的偏差最高约为10%．其中，由Bazant提出的老化系数计算公式确定的龄期调整的有效模量法的计算精度最高．

(3) 平均应力法高估了构件长期变形，其余简化方法则低估了长期变形，在钢管混凝土拱桥的设计施工中，为安全考虑建议采用平均应力法进行分析．

［1］ 肖雯雯. 考虑龄期影响的钢管高性能混凝土长期性能研究 [D]. 哈尔滨：哈尔滨工业大学土木工程学院，2008.Xiao Wenwen. Time-Dependent Behaviour of High-Performance Concrete Filled Steel Tube[D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2008(in Chinese).

［2］ Wang Y Y，Geng Y，Ranzi G，et al．Time-dependent behaviour of expansive concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research，2011，67(3)：471-483．

［3］ Uy B. Static long-term effects in short concrete-filled steel box columns under sustained loading[J]. ACI Structural Journal，2001，98(1)：96-104.

［4］ Goel R，Kumar R，Paul D K. Comparative study of various creep and shrinkage prediction models for concrete[J]. Journal of Materials in Civil Engineering，2007，19(3)：249-260.

［5］ Gilbert R I，Ranzi G. Time-Dependent Behaviour of Concrete Structures [M]. UK：Spon Press，2011.

［6］ 谭素杰，齐加连. 长期荷载对钢管混凝土受压构件强度影响的实验研究[J]. 哈尔滨建筑工程学院学报，1987，20(2)：10-24.Tan Sujie，Qi Jialian. Experimental investigation of the effects on the strength of concrete filled steel tubular compressive members under standing load[J]. Journal of Harbin University of Civil Engineering and Architecture，1987，20(2)：10-24(in Chinese).

［7］ Terrey P J，Bradford M A，Gilbert R I. Creep and shrinkage of concrete in concrete-filled circular steel tubes[C]//Proc of 6th Inter Symposium on Tubular Structures. Melbourne，Australia，1994：293-298.

［8］ Ichinose L H，Watanabe E，Nakai H. An experimental study on creep of concrete filled steel pipes[J]. Journal of Constructional Steel Research，2001，57(4)：453-466.

［9］ 林 军. 核心混凝土的徐变及其对钢管高强混凝土轴压构件力学性能的影响[D]. 汕头：汕头大学土木工程学院，2002.Lin Jun. The Creep of Core Concrete and Its Influence on the Mechanical Performance of the Axially Compressed High Strength Concrete Filled Steel Tubular Member[D]. Shantou：School of Civil Engineering，Shantou University，2002(in Chinese).

［10］ Kwon S H，Kim Y Y，Kim J K. Long-term behaviour under axial service loads of circular columns made from concrete filled steel tubes[J]. Magazine of Concrete Research，2005，57(2)：87-99.

［11］ Morino S，Kswanguchi J，Cao Z S. Creep behavior of concrete filled steel tubular members[C]// Proc of an Engineering Foundation Confer on Steel-Concrete Composite Structures. Irsee，Germany，1996：514-525.

［12］ 韩林海. 钢管混凝土结构——理论与实践 [M]. 2版． 北京：科学出版社，2007.Han Linhai. Concrete-Filled Steel Structure-Theory and Practice[M]. 2nd ed. Beijing：Science Press，2007(in Chinese).

［13］ Kwon S H，Kim T H，Kim Y Y，et al. Long-term behaviour of square concrete-filled steel tubular columns under axial service loads[J]. Magazine of Concrete Research，2007，59(1)：53-68.

［14］ 王 湛. 钢管膨胀混凝土的徐变[J]. 哈尔滨建筑工程学院学报，1994，27(3)：14-17.Wang Zhan. The creep for expansive concrete filled steel tube[J]. Journal of Harbin University of Civil Engineering and Architecture，1994，27(3)：14-17(in Chinese).

［15］ 姚宏旭. 大跨度钢管混凝土拱桥收缩徐变性能研究[D]. 长沙：湖南大学土木工程学院，2006.Yao Hongxu. Test Research on Shrinkage and Creep of Concrete Filled Steel Tubes on Long Span Arch Bridge[D]. Changsha：School of Civil Engineering，Hunan University，2006(in Chinese).

［16］ Bazant Z P，Baweja S. Creep and shrinkage prediction model for analysis and design of concrete structures：Model B3[C]// Adam Neville Symposium：Creep and Shrinkage-Structural Design Effects. Michigan，USA，2000：1-83.

［17］ Brooks J J，Neville A M. Relaxation of stress in concrete and its relation to creep[J]. ACI Journal，1976，73(4)：227-232.