手绘二维曲线自动生成三维模型研究
刘晓平, 吴 正, 李 琳
手绘二维曲线自动生成三维模型研究
刘晓平, 吴 正, 李 琳
(合肥工业大学计算机与信息学院VCC研究室, 安徽合肥 230009)
通过手绘创作三维模型是改变传统三维模型制作方式的新兴研究点;论文提出两种由手绘二维曲线自动产生三维模型的算法,分别进行了详细介绍和讨论:算法一基于重心原理拓展曲线,并在曲线簇上进行网格重构,但此方法仅限于椭圆拓扑的曲线;算法二利用离散方法寻找轴线,该方法能够生成更加多样化的模型并侧重于细节。通过算法实现效果的对比,验证了两种算法快速生成三维模型的有效性;最后展示了通过该文算法绘制的几个卡通模型,并对进一步生成模型动画进行了设想。
计算机图形学;手绘建模;网格化;卡通模型
三维模型是在计算机中构造虚拟对象的基本元素,有很多方法可以得到三维模型。美术创作人员利用三维建模软件如3DSMAX、MAYA按照一定的规则输入参数或者交互操作构造三维模型,但是此类软件一般操作很复杂,尤其对于自由曲面的构造;新出现的三维扫描仪可以得到现实景物的点云信息,但其数据量庞大,几乎无法应用在实时系统中;近年来还出现了基于图像的三维建模方法,成熟的技术大都体现在规则形体如楼房的构造上。简便快速直观的三维模型构造方法一直是图形领域长期关注的问题。
在二维美术创作中,由手写板进行输入绘制二维图像是美术人员的基本操作方式,这种方式接近于徒手绘图,符合美工的操作习惯,同时在二维笔触的识别与绘制方面也多有研究。由此得到启发,在三维模型的创作中,是否也能够利用手绘二维线条进行模型制作呢?很多学者开始了该方面的探索,较早的基于笔交互的建模系统SKETCH是一个基于鼠标的手势理解的几何建模体系,然而它所创建的几何模型仅局限于简单的图形,而且使用者必须严格遵循烦琐的操作顺序。其后出现了一个有意义的突破——Teddy,它开发了一个通过简单的轮廓绘制、填充、挤压变形等操作获得充分自由的三维图形的“人性化”工具,但其局限于具有椭圆轮廓模型的创建;现在的Teddy仍然在发展之中,已经到了第五代,但是仍然不足以成为商业化软件推广使用。国内在这方面也开展了许多有意义的工作,文献[6]将概念设计引入到三维模型的概念中,将基本的笔划操作保存到模型库,通过几何约束推理的方法识别创建三维模型,然而该算法必须建立合适的推理库,且操作不易理解。受阴影造型技术的启发,文献[7]提出了一种基于从明暗恢复形状的手绘草图三维建模方法,但由于需要对轮廓多边形组成的区域进行填充,并计算填充区域内每个像素点的灰度值和距离场而使算法显得非常复杂。由此可见,基于二维手绘产生三维模型是一个富有挑战而且应用面广影响力大的研究型问题,它的成熟将带来整个三维世界传统创作方式的彻底改变。
本文的主要工作是根据用户绘制的一个封闭自由曲线作为创建三维模型的基础轮廓,研究基于此轮廓线自动产生三维网格模型,达到平滑自由曲面的效果。由于一个三维网格模型需要点集信息与形成实体的面片信息,所以本文思想主要根据二维基础轮廓线向空间扩展,生成新的三维点集和面片集;由此提出两种基于手绘二维曲线生成三维模型的算法,分别为重心偏移法和轴线扩展法,与以上提及该方向的各种研究在思路上都有所不同;以下分别对这两种算法进行了详细的描述,并进行实验比较两种算法时间复杂度与生成模型的差异,给出两种算法下丰富的建模效果,分析两种算法的优势与劣势以及应用面的不同,最后给出一个具有挑战性的发展方向。
1 基于重心的三维模型生成算法
该算法考虑在绘制平面两边分别存在着一个基准点,轮廓线上的每一点可以向该基准点以椭圆法则扩展。首先求取轮廓线的重心,并将重心向绘制平面两边移动一定的距离作为基准点,然后以轮廓线上的每一点分别与基准点作为椭圆的两个端点插入新点,作为生成三维模型的组成点,网格化生成三角面片模型。
1.1 计算基准点
基准点以轮廓线重心为基础,设轮廓线点集二维坐标分别为(,),…,P(x,y),则重心为的坐标为
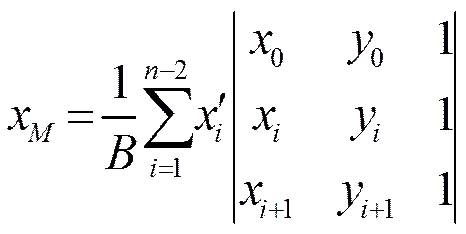
其中(1)
重心求出后,将其沿垂直于轮廓线平面的方向移动一定的距离作为轮廓线的基准点。如图1所示,点沿平面法向移动后得点。

(a) 二维轮廓线 (b) M为轮廓线重心 (c) 拔高作为轮廓线基准点
1.2 椭圆法则生成新点集
在计算得重心并基于重心得到基准点后,则对于轮廓线上任一点,点与点可作为椭圆的两个顶点构成四分之一椭圆曲线,如图2(a)。
设,,则按照椭圆公式1,则为四分之一段椭圆。用平行于轮廓线的平面按一定的间隔切割这些椭圆曲线,则每一次切割都会与这些椭圆线形成的个交点,完成次切割操作后,就会得到×个具有分层结构的新点集,如图2(b)。

(a) 椭圆法则 (b)生成的新点集
1.3 分层点云网格化
本算法最终形成的是三角面片模型,由于在点集生成过程中采取的切割椭圆线方法使得新点集存在着明显的分层结构,因此简化了网格化的难度。对于分层结构的点集,仅仅需要在相邻层之间构建网格,并且除基准点外,其余各层上点的数目与原始轮廓线点的数目相同。各层的点具有一一对应的关系,因而进一步简化了网格化的过程。构建网格的方法如图3所示。
设由点集,, …,A组成,由点集,, …,B组成,则网格化为三角形的数目为2,第2(0≤≤-2)个三角形和第21个三角形分别为△ABB与△ABA,第2(1)和第2(-1)+1个三角形分别为△AB和△AB,如图3所示。

(a) 相邻曲线之间构网 (b) 分层点集之间构网 (c) 最终网格
2 基于轴线的三维模型生成算法
该算法考虑为轮廓线上的每一个点找一个基准点,基准点集近似该轮廓线的一条轴线,可看作该轮廓线的“骨骼”。首先从二维点中的某个符合条件的点出发,逐步向前,求解得二维曲线的一条或多条类似于轴的曲线,使二维曲线的每个点对应于轴线上的相应基准点扩展。
2.1 基准线求取
基准线的求取是该算法的基础,它近似于轮廓线的轴线,存在于轮廓线的“中心”。对于给定的轮廓线,算法根据以下步骤求取基准点集:
如图4所示,找到具有最小内角度的角点,从点开始,逐步求得轮廓线上其他点的基准点。设的两个邻接点为、,不妨设,则在上存在一点',使得',连接',得到'的中点2,则2可以看作是和的中心线,并且取2是的基准点。由于是起始点,其基准点为本身。
处理完起始点后,待求取基准点的点为、,此时和的方向由与决定,为了计算或对应的基准点,算法首先求取与的中心线。设与的向量分别为,,则它们的中心线向量()()。
作者用向量垂直于中心线的直线过或切割轮廓线(不妨设过点切割),则该直线与另一边必交于一点(图中交交于),则两个交点的中点即为该点的基准点。在图4中,的中点1为的基准点。(如果直线在无交点,则过的直线必然与相交。)图4中,可由方程(2)解出。

其中为垂直于中心线的向量。如解得0≤≤1,则说明在解得,否则过点切割轮廓线。
图4 求解基准点的方法
找到的基准点后,待求取基准点的轮廓点为的后继点以及,重复前项操作直至处理完每个轮廓线上点的基准点,如图5所示。

图5 依次求解得所有基准点
2.2 新三维点集生成
基准线生成后,算法按下面方法生成构成模型的三维点集。对于轮廓线上的每一点,其对应在基准线上的基准点为,将沿着轮廓线平面的法线方向移动的距离,定义为四分之一圆弧,圆心为未在法线方向拉升前的,以平行于轮廓线平面的平面按适当的间隔切割该圆弧,获得的交点集为点扩展得到的新点集。处理完所有的轮廓线点后,即完成三维模型的新点集生成(见图6)。
图6 新点集生成的效果
2.3 点云网格化
由于该算法获得的基准线上的基准点拉升的距离不等,所以生成的新点集没有明显的分层结构。但由于每个轮廓线点对应一组新点集,因此算法采用最小对角线法在相邻的轮廓线点的对应点集之间构建网格。最小对角线法如图7所示。设,为轮廓线上的相邻点,其基准点为、,则在曲线上采集的点分别为,,…,P,在曲线上采集到的点分别为,,…,Q,使用最小对角线方法对两条曲线进行缝合。过程如下:
在最小对角线法构建网格过程中,设待建三角形的一条边为PQ为当前生长边,此时第三个点的选取原则为对角线最小,即PQ<QP时,则第三个点为Q,否则第三个点为P。再以PQ或QP为新的生长边继续生成三角形。形成的网格如图8所示。
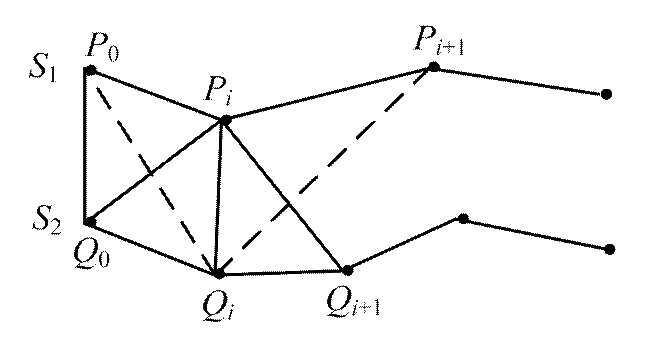
图7 最小对角线法

图8 网格化效果
3 实验结果分析
基于重心的三维模型生成算法计算较为简单,能够快速生成所需要的三维点和三角面片,对于圆形拓扑的轮廓线能够生成较好的效果,轮廓线上小的扰动不会影响到总体的效果。
但基于重心的三维模型生成算法难以处理非椭圆形拓扑结构的轮廓线,并且将轮廓线上所有的点都相对于同一基准点扩展显然不够合理。基于轴线的三维模型生成算法则试图找到一条或多条基准线,为每个轮廓线上的点找到一个基准点,有利于注重轮廓线的细节,并且扩展了算法的适用面。
重心偏移法和轴线扩展法的时间复杂度都是(),能够实时生成三维模型,其中为轮廓线点的个数,为生成新点集时切割曲线的层数。图9展示了两种算法生成模型的效果,左边为轴线扩展法,右侧为重心偏移法。可见,在相同级别的时间复杂度下,轴线扩展法对于非椭圆结构的轮廓线具有更好的生成效果。

另外,基于轴线的三维模型生成算法中形成的轴线可以用来设计模型的动画序列,为扩展到动画功能提供了必要的条件。
4 总结与展望
近两年,抛弃鼠标与键盘,直接通过笔触与手势与计算机进行交互已经成为人机交互的主要方式,APPLE IPHONE和即将到来的WINDOWS7无一不体现着这一理念。本文提出的方法正是顺应这一交互手段,提出一种新的创建三维光滑曲面模型的方法,用户不需要操作控制点或者进行复杂的编辑操作就可以得到理想的结果,信手涂鸦的方式适用于非专业人士或者是灵感形成阶段的记录。本文方法所产生的结果非常适合于各种卡通对象的绘制,为卡通模型的制作提供了一种简洁快速的创作途径,由于卡通模型是动漫创作的重要组成部分,因此本文的研究对动漫行业也具有非常重要的意义和实用价值。图10是利用本文算法生成的卡通模型实例。

图10 生成的卡通模型展示
本文的工作只是手绘产生三维模型的一个开始,作者将对算法进一步改进,以适应于更多的复杂情况。而在第二种算法中出现的“轴线”,将对产生以骨骼为基础的三维动画有着极大的价值,进一步研究基于轴线的动画序列的产生,最终形成从手绘建模到动画生成的一整套系统是作者最终的目标。
[1] 任秉银, 陈皓晖. 任意拓扑结构复杂曲面模型重构新方法[J]. 机械工程学报, 2003, 39(10): 162-166.
[2] Levoy M, Pulli K, Curless B, et al. The digital michelangelo project: 3D scanning of large statues [C]//Siggraph, 2000: 131-144.
[3] Esteban C H, Schmitt F. Silhouette and stereo fusion for 3D object modeling [J]. Computer Vision and Image Understanding, 2004, 96: 367-392.
[4] Zeleznik R C, Herndon K P, Hughes J F. SKETCH: an interface for sketching 3D scenes [C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, New Orleans, 1996: 163-170.
[5] Igorashi T, Mat suoka S, Tanaka H. Teddy: a sketching interface for 3D freeform design [C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angels, 1999: 409-416.
[6] 韩 丽, 唐 棣. 手绘输入的三维建模和编辑技术[J]. 计算机辅助设计与图形学学报, 2008, 20: 946-951.
[7] 谢 浩, 费广正, 吴明峰, 等. 从明暗恢复形状的手绘草图三维建模算法[J]. 工程图学学报, 2006, 27(4): 57-65.
[8] Eggli L, Hsu C, Elber G, et al. Inferring 3D models from freehand sketches and constraints [J]. Computer-Aided Design, 1997, 29(2): 101-112.
[9] Ku D C, Qin S F, Wright D K. Interpretation of overt racing freehand sketching for geometric shapes [C]//Proceedings of Computer Graphics, Visualization and Computer Vision 'WSCG', Plzen, 2006: 263-270.
[10] Qin S F, Wright D K. Progressive surface modelling scheme from unorganised curves [J]. Computer Aided Design, 2006, 38(10): 1113-1122.
Automatic Generation of 3D Model Based on Sketch
LIU Xiao-ping, WU Zheng, LI Lin
( VCC Division, School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China )
Creating 3D model based on sketch is an emerging research that changes traditional modeling pattern. Two algorithms of automatic generation of 3D model based on 2D curve sketching are introduced and discussed in detail in this paper. The first one expands the curve based barycenter, then reconstructs a mesh from curve-cluster, which, however, is limited in application to only ellipse-like topology curves. The second one finds its axis using discrete method, so more diversified models focusing on details can be generated. The comparison of realization effects of the two algorithms shows that they are effective for fast generation of 3D. Finally, several cartoon models created by the algorithms are displayed, and generation of model animation are desired for further.
computer graphics; sketch-based modeling; triangulation; cartoon model
TP 391
A
1003-0158(2011)03-0017-06
2009-12-12
国家自然科学基金国际(地区)合作交流资助项目(60573174);特种显示技术教育部重点实验室开放课题基金
刘晓平(1964-),男,山东济南人,教授,主要研究方向为建模、仿真与协同计算。

