多元主成分和动态聚类在油菜常规试验主要性状分析中的应用

万林生，单忠德，孙红芹，倪正斌

(江苏省沿海地区农业科学研究所，江苏 盐城 224002)

随着育种工作越来越精细化，传统育种依赖肉眼判断和唯一产量高低判断已经显示出越来越多的弊端。本研究通过将多元统计分析方法中的主成分分析和动态聚类分析联合分析，对多性状资料进行降维，通过线性组合，提炼出较少几个彼此独立的2～3个主成分，并对提炼出来的几个主成分进行动态聚类分析，将品种或者育种材料进行分类，从而选择与对照一类或者超越对照性状的几类进行进一步的研究。该研究打破了育种中仅以产量高低为唯一标准选择材料的传统，为传统育种的量化分析提供了一个新的思路。同时，采用聚类分析可以避免当选育品种数目较多时采用方差分析产量产生的自由度不单一的错误。研究并以2009－2010年江苏省常规油菜预备试验14个品种(含对照)为数据资料，阐明分析的具体过程。

1 材料与方法

1.1 主成分分析和动态聚类分析

主成分分析又称主分量分析，是指将原始的多个变量，通过线性组合，提炼出较少几个彼此独立的新变量的一种多元统计方法［1］。通常数学上的处理就是将原来p个指标作线性组合，成为新的综合指标，第1线性组合即第1个综合指标记作Y1，Y1的方差越大，包含的信息越多，方差最大的称作第1主成分，若Y1不足以代表原来p个指标的信息，则考虑第2主成分，即Y2，以此类推。主成分分析的作用:降低所研究的数据空间的维数，多维降为少维并用图形直观表示;便于解释，把所研究的性状串起来，我们可以得到产量主成分、形态性状主成分、生育期主成分等等;构建选择指数［2］。

主成分分析的计算一般分为4个步骤。

第1步计算方差协方差矩阵。对于一组n个个体p个性状的数据资料，

计算该数据资料的方差协方差矩阵:

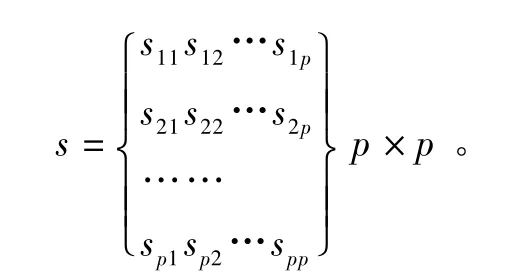
第3步计算主成分贡献率及累计贡献率。

第4步计算主成分得分。

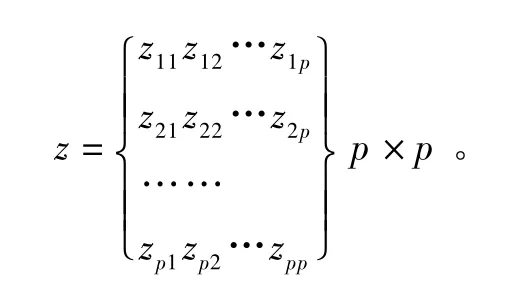
聚类分析指将物理或抽象对象的集合分组成为由类似的对象组成的多个类的分析过程。一般可分为系统聚类与动态聚类。

系统聚类是先假定各个样品各自成一类，这时各类间的距离就是各样品之间的距离，将距离最近的2类合并成一个新的类，再计算新类与其它类间的距离，将距离最近的2类合并，如此每次缩小一类，直至所有的样品都成为一类为止［3］。然后根据需要或者根据给出的距离临界值确定分类数及最终要分的类。该聚类方法一般有最短距离法、最长距离法、中间距离法、重心法、组平均法、最小组内平方和法等。但系统聚类存在较为严重的缺陷:每种聚类由于聚类递推公式参数取值不一致，故聚类结果不是唯一的;(最短距离法、最长距离法、中间距离法、重心法分类不具有单调性;系统聚类的主观性较强，假如要求类与类之间的距离大于给定的阈值I，有些样品很有可能会因此而归不了类或只能自成一类［4－5］。

动态聚类其基本思想:选择一批凝聚点或给出初始的分类，让样品按某种原则向凝聚点凝聚，对凝聚点进行不断的修改和迭代，直至分类比较合理或迭代比较稳定为止。类的个数k可以事先指定，也可以在聚类过程中确定。一般重心法(K-means法)和最小组内平方和法(SSW)这2种方法使用的比较多。但是重心法不稳定性，不同的初始聚类给出在分类较多的情况下往往具有不同的分类结果。最小组内平方和法我们设想假如分类是合理的，其最终结果应该是达到各组内平方和最小，即组间平方和最大［6］。

1.2 数据资料

表1即为2009－2010年江苏常规预备试验14个品种(含对照品种红油3号)11个性状的数据资料，数据均为田间考种结果。

表1 2009－2010年江苏常规预备试验14个品种11个性状的数据

2 结果和分析

2.1 主成分

利用Matlab软件进行主成分分析，结果前3个综合指标的贡献率分别为86.72%、8.19%和2.65%，总的贡献率达97.56%，说明前3个综合指标基本反映了11个指标的全部信息。它们所对应的第1－3主成分特征向量:Y1=－0.014 6X1+0.128 3X2－0.02X3－0.019X4－0.001 4X5－0.071 2X6－0.968 0X7－0.201 0X8+0.021X9－0.001 9X10+0.002 5X11;Y2= －0.673 1X1－0.589 8X2+0.017 8X3+0.012 6X4－0.323 4X5－0.284 6X6－0.067 0X7+0.090 2X8－0.085X9+0.019 0X10－0.002 7X11;Y3= －0.048 9X1－0.051 9X2－0.010 8X3－0.090 4X4－0.129 1X5+0.010 2X6+0.194 9X7－0.962 6X8－0.013 5X9－0.071 1X10+0.000 4X11。

Y1在1次分枝结角、2次分枝结角、分枝点高度等性状上所占的比重较大，Y2在株高、分枝点高度、主轴长度、主轴有效角果等性状上所占的比重较大，Y3在主轴长度、1次分枝结角、2次分枝结角等性状上所占的比重较大。

2.2 动态聚类

对前3个主成分进行动态聚类分析，结果如图1－4所示。

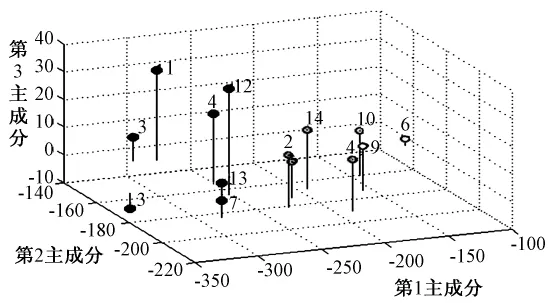
图1 分3类的聚类结果

图2 分4类的聚类结果

图3 分5类的聚类结果

图1 分为3类，SSW=1.330 3×104，1，3，4，7，8，12，13;2，5，11，14;6，9，10 各 为1类。图2分为4类，SSW=9.058 3×103，1，3，4，12;7，8，13;2，5，11，14;6，9，10 各为1类。图3分为5类，SSW=5.065 0×103，1，3，4，12;7，8，13;2，5，11，14;9，10;6各为1类。图4为分为6类的结果，SSW=3.532 7×103，1，4，12;3，8;7，13;2，5，11，14;9，10;6各为1类。每1类所包含的序号即为所对应的品种编号。

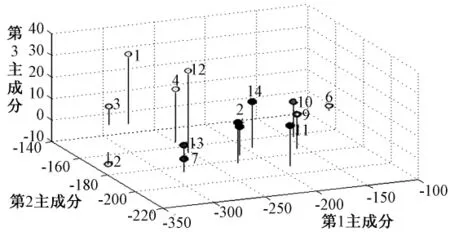
图4 分6类的聚类结果

3 小结

本研究主要通过多元统计分析方法中的主成分分析和动态聚类分析对2009－2010年江苏省常规油菜预备试验14个品种的11个主要性状进行研究。结果表明:主成分分析的前3个主成分Y1，Y2，Y3含有总的贡献率达到97.56%，并且通过3大主成分分别在各个性状中的得分值的高低了解各个性状在主成分中的分量。将主成分的前3个主成分进行基于组内平方和最小的动态聚类分析，得到唯一聚类结果，并根据分类数的不同画出不同颜色聚类图形。本研究给传统育种的量化分析提供了一个新的思路。

本研究重点介绍将多维彼此无关的数据线性简化形成的主成分分析与准确唯一的动态聚类分析结合在一起形成了良好的多元数据分析体系，并以油菜杂交预试主要性状数据为例，更加直观地分析该体系的运作方式和方便之处，为推广该系统方法打下了基础。

［1］韩继祥，刘后利．甘蓝型油菜杂种主要农艺性状和品质性状的主成分分析［J］．华中农业大学学报，1993(5):31－36.

［2］段利云，王通强，阳标仁，等．甘蓝型油菜主要农艺性状的主成分和聚类分析［J］．山地农业生物学报，2007(5):9－13.

［3］丁厚栋，张尧锋，余华胜，等．甘蓝型油菜种质资源的农艺性状聚类分析［J］．华北农学报，2009(增刊 1):109－111.

［4］林宝刚，丁厚栋，张尧锋，等．国外甘蓝型油菜种质资源农艺性状和品质性状的聚类分析［J］．中国种业，2010(4):49－51.

［5］刘定富．甘蓝型油菜品种的聚类分析［J］．湖北农学院学报，1993(3):13－19.

［6］宋来强，贺兴文．甘蓝型油菜亲本材料的综合评价和聚类分析［J］．江西农业学报，1990(1):41－48.