螺旋锥齿轮机床五轴联动数学模型创成算法

唐进元，聂金安，王智泉

(中南大学 机电工程学院，现代复杂装备设计与极端制造教育部重点实验室，湖南 长沙，410083)

机械式螺旋锥齿轮加工机床结构复杂，调整参数繁冗，传动链为机械传动，精度等级低。五轴联动型机床与机械型机床相比，机床体积减小，加工精度提高，可操作性增强。五轴联动型机床采用五轴联动来拟合机械型的摇台运动和刀倾刀转的运动变化，实现了全数控控制[1]，将复杂的加工运动通过数控轴的联动来实现，提高了控制精度与加工精度。目前，有许多学者对2类螺旋锥齿轮加工机床的运动转换关系进行了研究。Goldrich[2]提出了机械式机床与五轴联动型机床的等效转换思想，由于考虑到商业秘密没有给出任何转换公式和计算方法；Litvin等[3]随后提出耦合2种机床坐标系使2种机床运动关系完全等效的原理，但没有给出各轴运动方程的求解算法；张艳红等[4]在齿面参考点进行转换，通过高阶科氏加速度方法研究了机械型向五轴联动型机床的模型转换问题；魏冰阳等[5]在 litvin基础上推导了机械型向五轴联动型机床的显式转换公式，但此法仅对无刀倾刀转的直接展成法有效，基于刀倾法的机械型向五轴联动型机床的转换比展成法要困难得多；张威等[6]继承文献[4]的思想与方法，用矢量旋转方法，通过矩阵导数理论对麦克劳林级数中的导数进行近似求解替代，近似得到刀倾法加工时各轴的运动方程。这种方法由于需要对转换方程中的导数进行近似求解，理论上存在原理性误差，转换的精度受到影响。本文作者以Litvin方法为出发点，基于运动等效与位置等效原理，建立从机械型到五轴联动型机床的数学转换模型，得到一组五轴联动型机床各轴的非线性运动方程；通过麦克劳林级数拟合机床各轴的非线性运动方程，在拟合过程中直接求取麦克劳林级数中的导数项，最终得到各轴运动方程的多项式形式，转换精度可以根据多项式阶次控制。

1 2类机床加工调整参数的转换原理

在切齿过程中，假想有1个平顶齿轮与机床摇台同心，它通过机床摇台的转动而与被切齿轮进行无隙啮合。该假想平顶齿轮的轮齿表面由铣刀盘刀片切削刃相对于摇台运动的轨迹表面所代替，在相对运动过程中，代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐切出齿形[7]。

一种相对运动关系是不依赖于所建立的旨在描述这种运动的参考系而存在的[8]。以相同加工原理进行的各类数控机床的螺旋锥齿轮加工运动是为了实现该相对运动，使刀具与轮坯以符合加工原理的运动规律来完成相对运动。

2类机床的转换原理(即保证刀具和轮坯在任意时刻的相对位姿恒定)[9]如图1所示。本文中保证刀盘轴线和轮坯轴线在任意时刻的夹角和固定点之间的长度矢量相等。

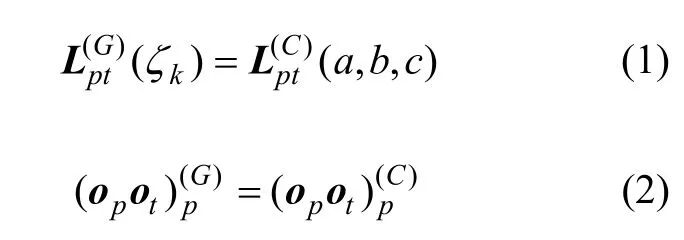
式中：Lpt为标架St到Sp的旋转变换矩阵；(opot)p为轮坯轴交错点到刀盘中心在轮坯坐标系下的矢量长度；上标C和G分别代表五轴联动机床加工过程和机械型加工小轮的展成过程，下标p和t代表坐标系。式(1)保证了2种刀具相对于工件运动姿态相同，式(2)保证了两者的相对位置相同。

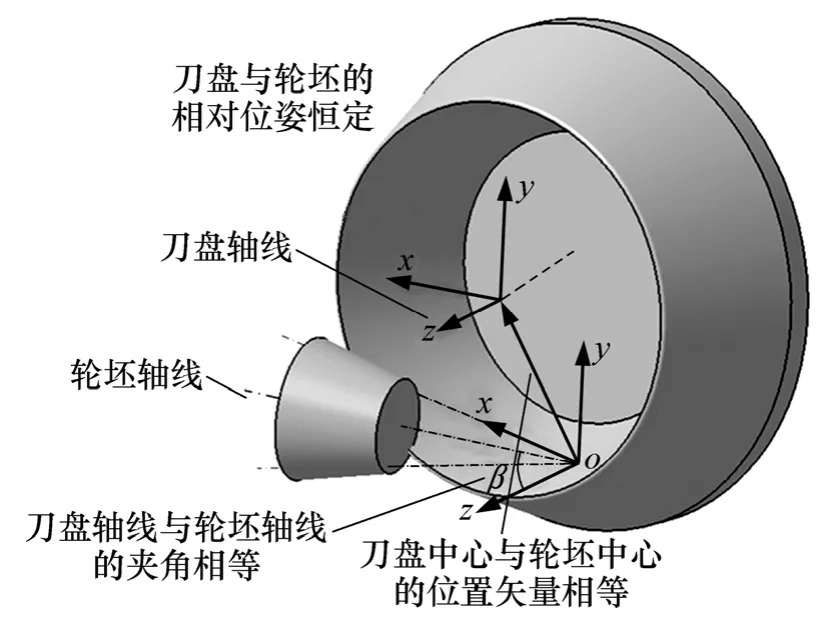
图1 2种类型机床的转换原理Fig.1 Transform theory between two machines

2 机械式机床的数学模型

传统摇台机床结构如图2所示，其调整参数十分复杂。加工坐标系如图3所示[10]，其中：So(xo，yo，zo)为与床身固连的坐标系；Sc(xc，yc，zc)为与摇台固连的坐标系，且原点为摇台中心；Sp(xb，yb，zb)为与刀盘固连的坐标系；Sp(xp，yp，zp)为与工件固连的坐标系；Se(xe，ye，ze)为与工件箱固连的坐标系；Sn(xn，yn，zn)为与床鞍固连的坐标系，其原点On在So中用坐标(0，-Em，Xb)来表示；Sq(xq，yq，zq)是过渡坐标系，各个坐标轴与Sn平行，其原点Oq在Sn中用坐标(X1，0，0)来表示；Sc绕zc有1个转角q；Sp绕xp有1个转角φp；Se绕ye有1个转角rm；q为角向刀位；i为总刀倾角；j为基本刀转角；Em为垂直轮位；Sd为径向刀位；rm为安装根锥角；X1为水平轮位；Xb为床位；C为刀盘中心(刀盘旋转轴与刃平面的交点)。机床调整参数为螺旋锥齿轮加工的基本参数，本文以最复杂的刀倾法加工小轮为例，具体数值见表1。

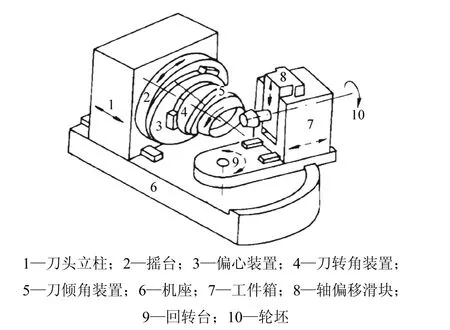
图2 传统机械式摇台型机床及运动部件Fig.2 Conventional machines consisted of many components

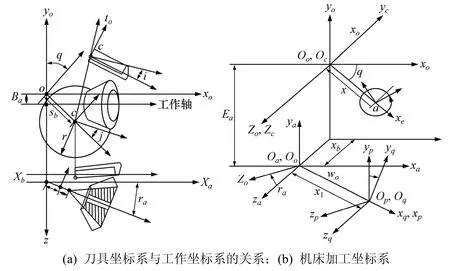
图3 机械式摇台机床加工坐标系Fig.3 Coordinate systems for mechanical machine

由传统摇台式机床加工调整参数的计算，可以建立如下各矢量的表达式：

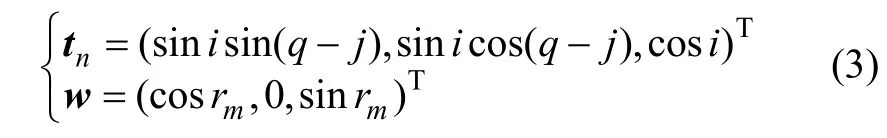
式中：tn为刀盘旋转轴单位矢量，过刀盘中心C并指向刀盘外部；w为工件旋转轴单位矢量，指向远离锥顶方向。

由Descartes坐标变换，可得到刀盘坐标系到轮坯坐标系的变换矩阵，即可得到 (o )和L(ζ)。 t k其中：ζk代表传统机床各调整参数，具体数值见表1。

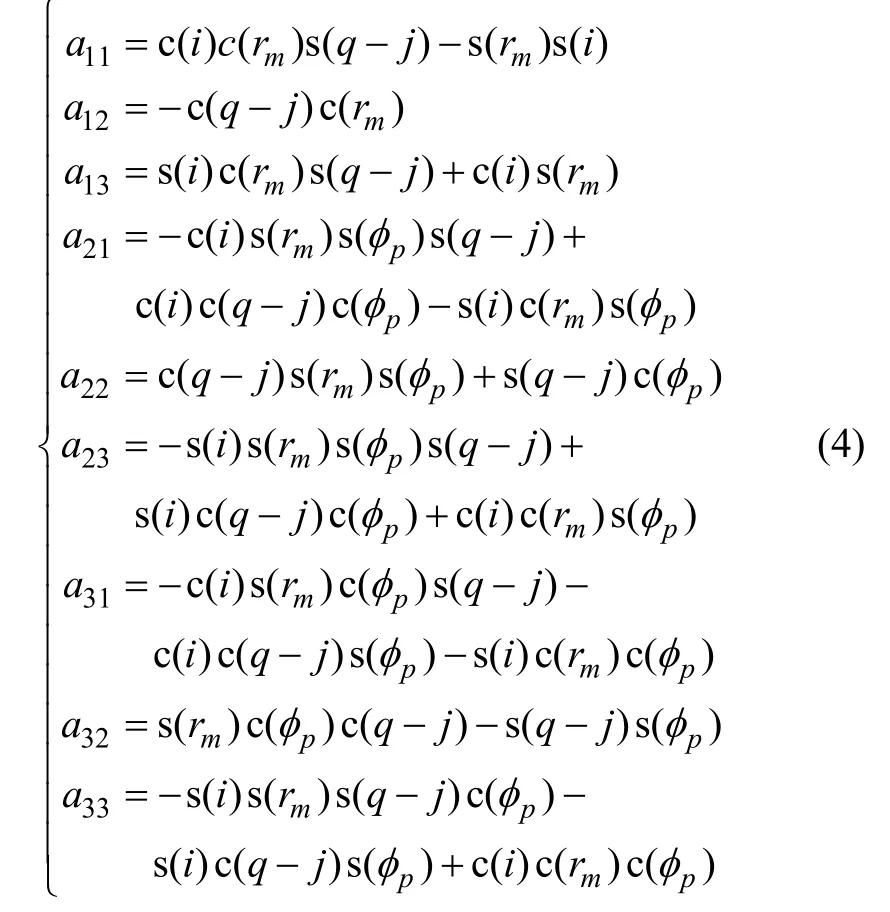
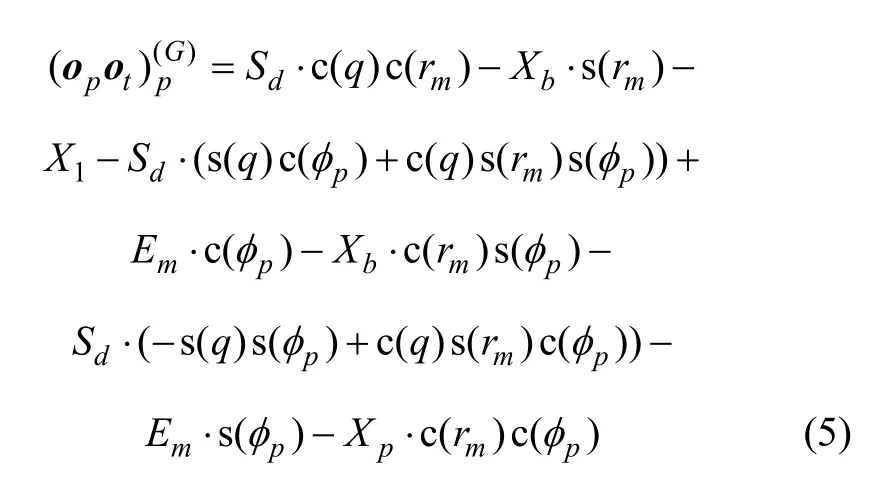
3 五轴联动机床的数学模型

五轴联动机床用6坐标轴实现了齿轮加工的全部运动，机床结构如图4(a)所示即3个平动轴(X，Y，Z)和3个转动轴(A，B，C)，提供 6个自由度，可灵活地控制工件与刀具在空间中的位置和运动。

首先建立如图 4(b)所示的一组坐标系[11]。Sf(Xf，Yf，Zf) 与床身Ⅴ固联；St(xt，yt，zt)和 Sp(xt，yt，zt)分别与刀盘、工件固联；Sh和 Sm与 Sf平行，分别与 Y方向滑台Ⅰ和Z方向滑台Ⅲ固联；Sh原点oh在Sf中的位置，用坐标(x，y，0)表示，描述X和Y自由度；Sm原点 om在 Sf中的位置用坐标(0，0，z)表示，描述 Z自由度；St绕坐标轴zh转动(即C旋转自由度)转角c；Se与转台Ⅳ固联，绕 ym轴有一转角 b(即 B旋转自由度)；Sd为过渡坐标系与Se坐标轴平行，原点 od位置由 L(对应机械式摇台机床中的水平轮位)确定；Sp绕xd轴做旋转(即A旋转自由度)，转角为a。通过坐标变换即可得到 (o )和L(a,b,c)。

PHOENIX I型五轴联动数控机床各部件的运动

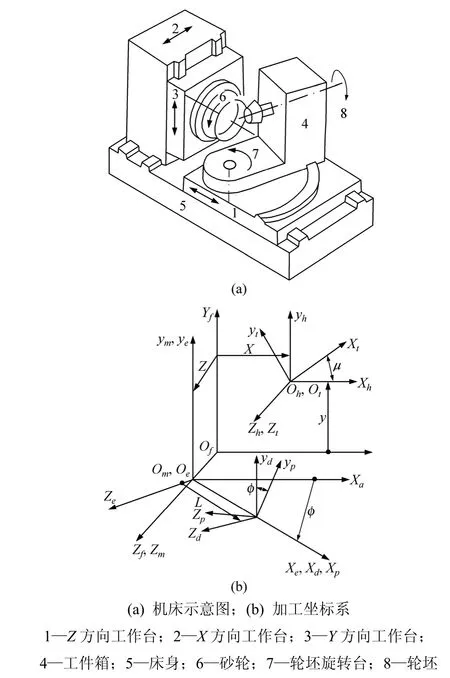
图4 PHOENIX I型五轴联动机床加工坐标系Fig.4 Coordinate systems for PHOENIX I Machine

转换矩阵如下：

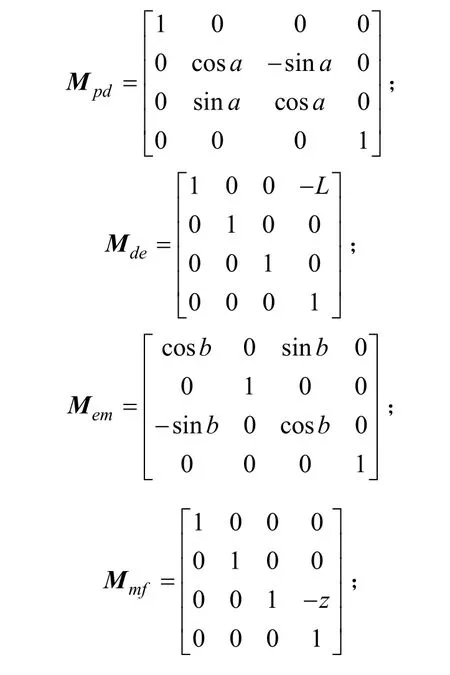
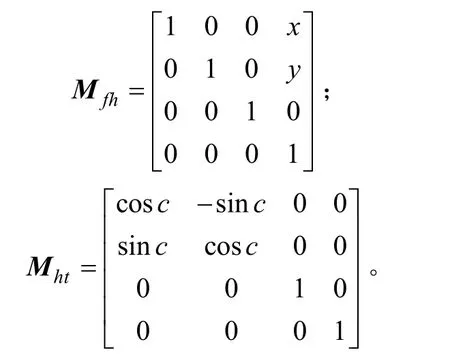
则PHOENIX I型机床坐标系下刀盘到轮坯坐标系的转换矩阵如下：

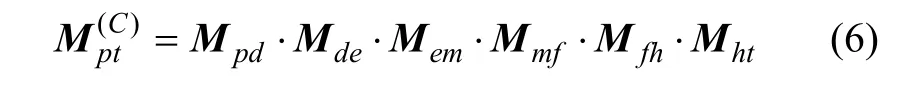
由于刀具到轮坯坐标系的转换矩阵可以表示为：

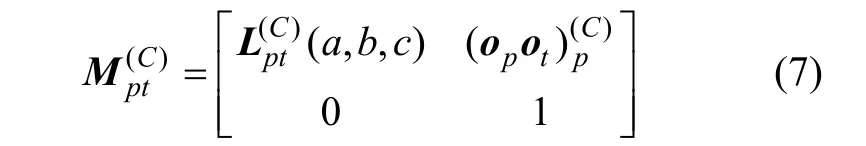
则有角度旋转变化矩阵和长度矢量为：

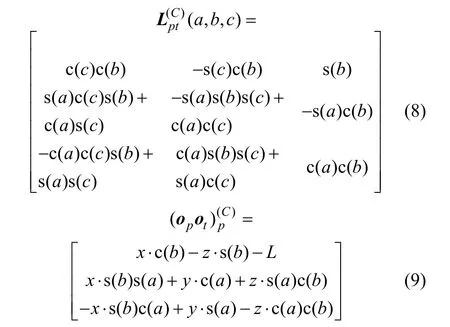
4 不同加工方法的五轴联动机床运动参数的求解

由式(1)知式(4)和(8)对应各矩阵元素相等，由式(2)知式(5)和(9)对应各矩阵元素相等，可求出都是关于t的函数。

(1)当无刀倾刀转即i=0，j=0时，得Phoenix I的运动参数如下：

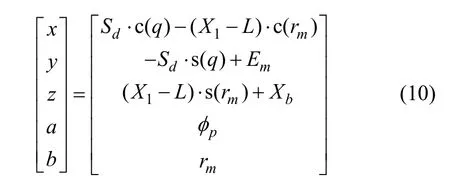
(2) 当用变性法加工时，仅改变 2个量之间的比例关系，通过修正滚比，使螺旋锥齿轮的传动误差满足预先设计的高阶几何传动误差曲线。此种情况下，仅改变φp与t之间的比例关系，将φp代入式(10)即可。

(3) 当具有刀倾刀转角加工螺旋锥齿轮时，通过耦合2种机床坐标系求得各轴运动方程的解析解，如式(11)所示。

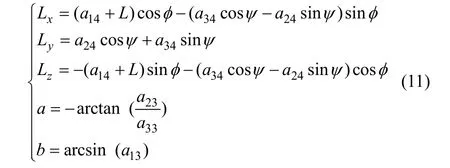
通过一组麦克劳林级数简化上述表达式，如式(12)，可以求得近似的多项式表达形式，级数阶次 n的选取根据所需精度确定。t=0时刻表示刀盘位于初始摇台角位置。

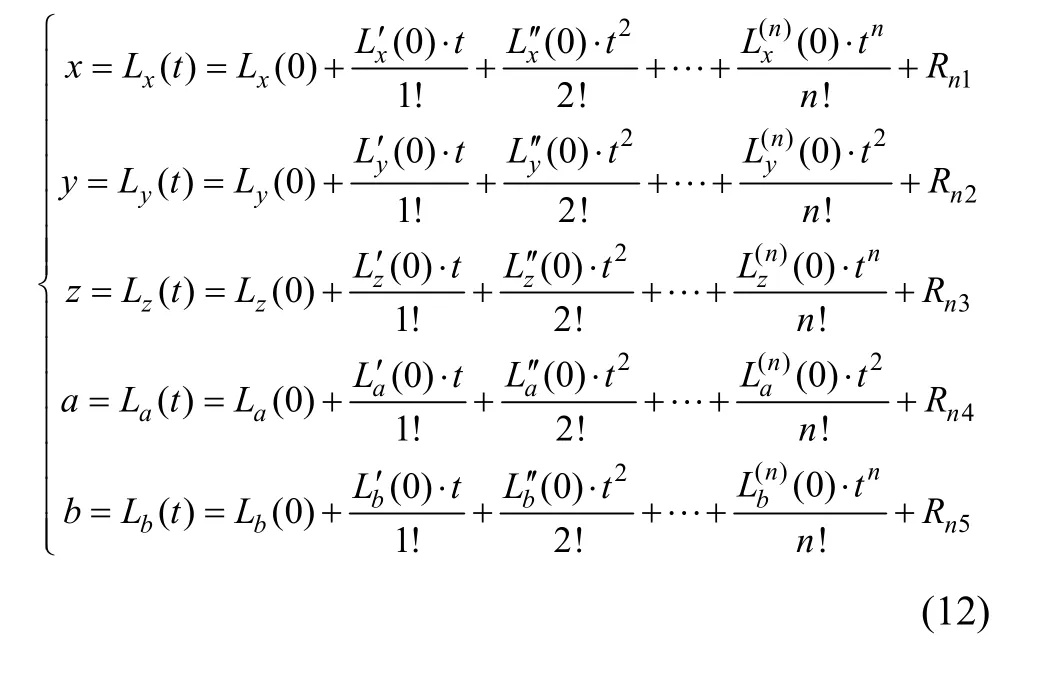
5 实例分析

螺旋锥齿轮数学模型是根据啮合理论和相对应的加工方法而建立的。从建立数学模型的角度来考虑，对于小轮采用刀倾法加工建立的齿面数学模型，可以作为大轮和小轮的通用数学模型，其他加工方法的数学模型可以看作是其特例，如将刀倾法建立的锥齿轮数学模型中刀倾斜角和刀转角设置为0°，可看作是展成法加工大轮的数学模型；将小轮对大轮的偏置距设为 0 mm，则准双曲面齿轮实际上就变成了弧齿锥齿轮；若大轮在这个数学模型中滚比为 0，就成了大轮成形法加工。

下面以某准双曲面齿轮副的小轮为例，用本文方法将刀倾法调整参数转换为五轴联动型机床五轴运动方程。齿轮副的刀倾法调整参数见表 1，转换后五轴联动机床主轴方程见表2，转换精度取10-3。

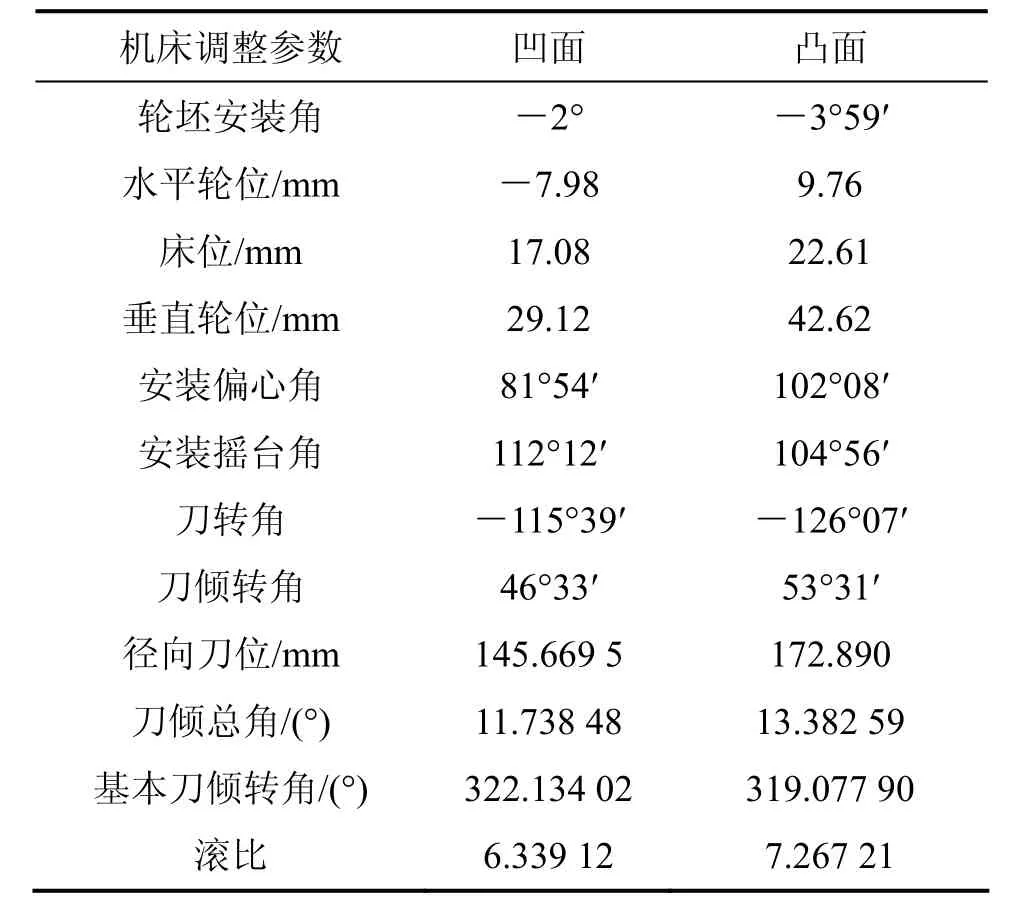
表1 轮坯设计与机床调整参数(HFT调整卡)Table 1 Parameters and installment settings of pinion (HFT)

表2 凤凰I型数控机床加工小轮各主轴控制方程Table 2 Motions of Gleason PHOENIX I machine axes

用 θ代表刀具与工件轴矢量相对姿态(夹角)，则在传统坐标系中，θ由式(3)中刀具轴与工件轴的点积求出，在凤凰一代机床中由B轴表达式求出。夹角θ在机械型机床坐标系和凤凰一代机床坐标系中的余弦变化曲线及其差值如图5所示。

由图5可以看出：θ在这2种机床坐标系下，其余弦曲线基本重合。在螺旋锥齿轮的1个加工周期内，余弦曲线的差值在 10-3以内(此时麦克劳林级数的阶次n=5)，远小于机床本身的运动误差。

长度矢量(opot)p在1个加工周期中在2种机床坐标系下的矢量差值见图6。由图6可知：其数量级在10-8mm以内，转换精度高。

通过 θ余弦曲线和不同机床坐标系中长度矢量(opot)p差值可知：简化后的近似模型完全满足螺旋锥齿轮的高精度加工。下面以GLEASON公司软件计算结果为标准，对转换精度进行进一步验证。

利用求解得到的凤凰I型数控机床的各主轴控制方程，根据本文提出的齿轮虚拟制造方法[12]，在虚拟制造系统中可以加工出1个仿真的小齿轮(见图7)。通过GLEASON公司软件计算出本套调整卡加工齿轮的理论齿面，按照格里森测量全齿面误差方法[13]，选取如图7所示的45个点，并建立近似模型与理论齿面的差曲面[14]，如图8所示。从图8可见：当n=5时，本文的近似模型与理论齿面在齿面法矢方向的偏差在±1.5×10-4mm以内。在实际加工中，齿面的最大法向误差在10 μm左右，本文的转换模型对螺旋锥齿轮的齿面修正所带来的误差可以忽略，因此，在螺旋锥齿轮的实际加工和齿面修正中，本文提出的转换模型是有效的。

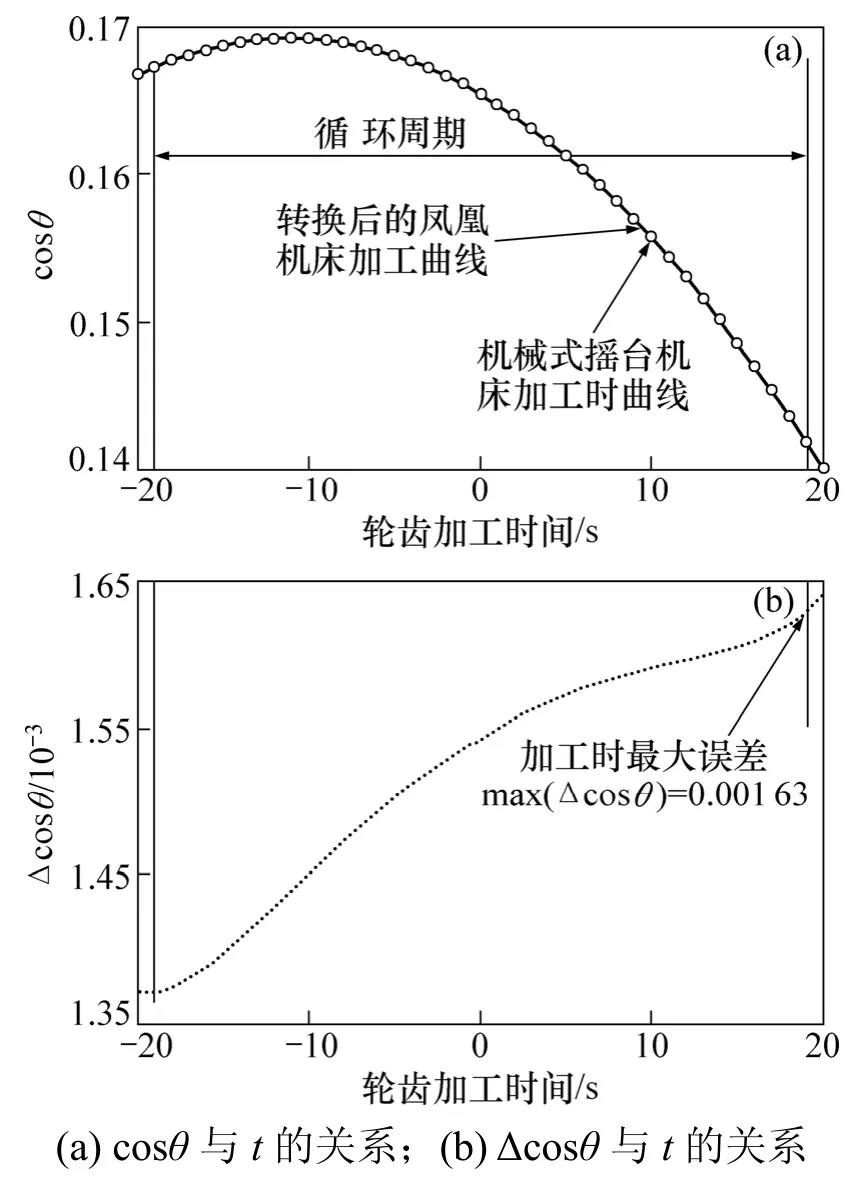
图5 不同机床坐标系中θ角余弦曲线Fig.5 Transformation error of angle between two machines

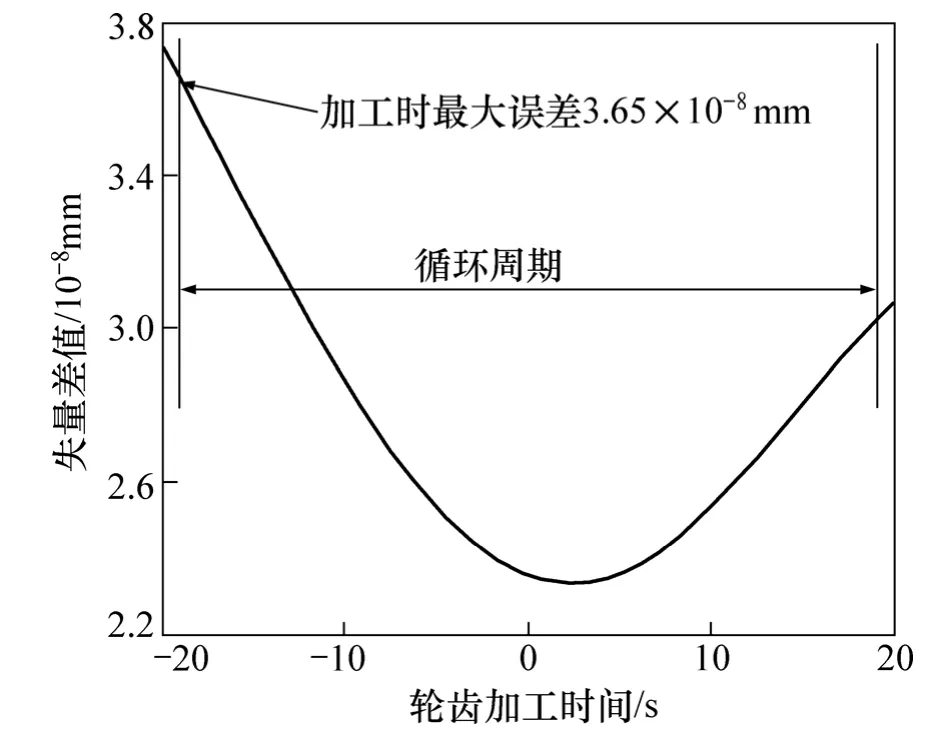
图6 不同机床坐标系中长度矢量(opot)p差值Fig.6 Transformation error of vetor between two machines

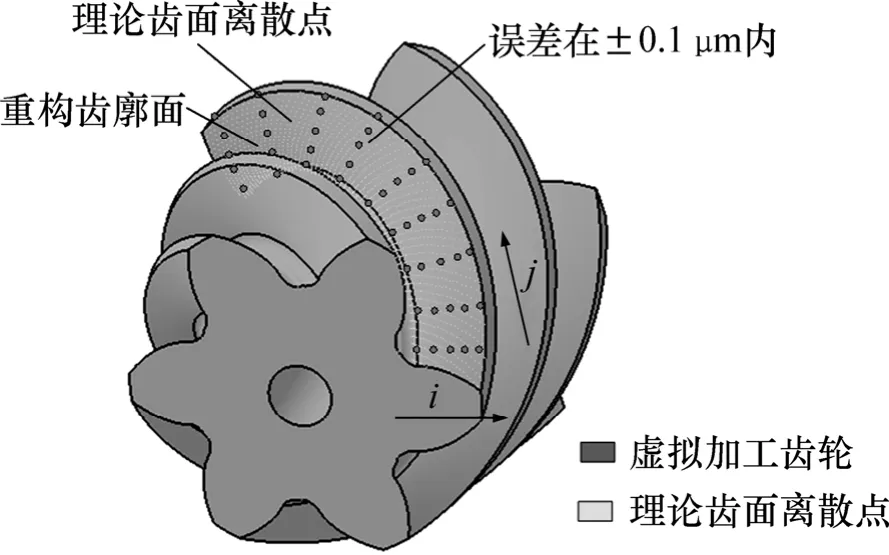
图7 虚拟制造小轮与理论点的比较Fig.7 Flank topographic deviations derived by comparing theoretical teeth-surface and virus manufacturing pinion

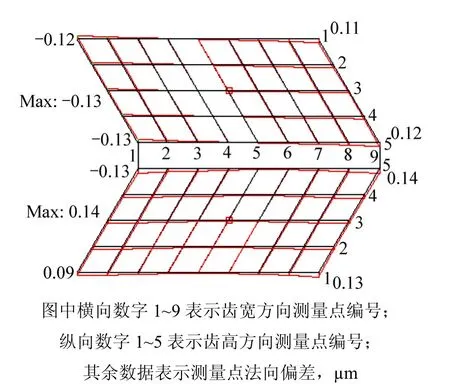
图8 全齿面法向误差分析Fig.8 Flank form errors analysis

6 结论

(1) 通过麦克劳林级数拟合机床各轴的非线性运动方程，在拟合过程中直接求取麦克劳林级数中的导数项，最终得到各轴运动方程的多项式形式。转换精度可以根据多项式阶次控制。所提出的方法避免了现有方法存在的原理性误差。

(2) 给出从机械式摇台机床求解到五轴联动数控机床的五轴联动控制模型生成方法。该方法具有精度高、可操作性强的特点。通过实例计算分析，验证了所给出方法的可行性与正确性，为螺旋锥齿轮数字化制造提供了基础技术。

[1] 樊奇, 让·德福. 格里森专家制造系统(GEMS)开创弧齿锥齿轮及双曲面齿轮数字化制造新纪元[J]. 世界制造技术与装备市场, 2005, 79(4): 87-93.FAN Qi, Dafoe R. Gleason expert manufacturing system (GEMS)opens a new era for digitized manufacturing of spiral bevel and hypoid gears[J]. World Manufacturing Engineering & Market(WMEN), 2005, 79(4): 87-93.

[2] Goldrich R. Theory of 6-axis CNC generation of spiral bevel and hypoid gears[R]. New York: The Gleason Works, 1989: 23-30.

[3] Litvin F, Chen N, Nag U. Generation of gear tooth surfaces by application of CNC machines[R]. Chicago: University of Illinois at Chicago, 1994: 20-35.

[4] 张艳红, 吴联银. 刀倾型机床调整参数转化为 Free-Form 型机床调整参数的原理[J]. 机械科学与技术, 2000, 19(5):782-784.ZHANG Yan-hong, WU Lian-ying. On the theory of transformation machine setting parameters from cutter-tilt milling machine to Free-Form milling machine[J]. Mechanical Science and Technology, 2000, 19(5): 782-784.

[5] 魏冰阳, 任东锋, 方宗德, 等. 传统机床与五轴联动型机床运动的等效转换[J]. 机械科学与技术, 2004, 23(4): 425-428.WEI Bin-yang, REN Dong-feng, FANG Zong-de, et al. Study on kinematic equivalent transformation from traditional machine tools to five-axis linkage ones[J]. Mechanical Science and Technology, 2004, 23(4): 425-428.

[6] 张威, 王太勇, 罗珺, 等. 面向刀倾展成法的运动学转换简化算法及仿真[J]. 机械工程学报, 2008, 44(3): 123-129.ZHANG Wei, WANG Tai-yong, LUO Jun, et al. Kinematics transformation for tilt generated method and simulation[J].Chinese Journal of Mechanical Engineering, 2008, 44(3):123-129.

[7] Shih Y, Fong Z, Lin G. Mathematical model for a universal face hobbing hypoid gear generator[J]. Journal of Mechanical Design,2007, 129(1): 38-47.

[8] 熊有伦, 唐立新, 刘恩沧, 等. 机器人技术基础[M]. 武汉: 华中理工大学出版社, 1996: 25-35.XIONG You-lun, TANG Li-xin, LIU En-cang, et al. Foundation of robot technology[M]. Wuhan: Huazhong University of Science and Technology Press, 1996: 25-35.

[9] Litvin F, Fuentes A. Gear geometry and applied theory [M].London: United Kingdom Cambridge University Press, 2004:83-150.

[10] Stardtfeld H J. Handbook of bevel and hypoid gear[M]. New York: Rochester Institute of Technology Press, 1993: 190-200.

[11] FAN Q. Computerized modeling and simulation of spiral bevel and hypoid gears manufactured by gleason face hobbing process[J]. Journal of Mechanical Design, 2006, 128(6):1315-1327.

[12] 蒲太平, 唐进元. 基于 CATIA V5 的圆柱齿轮虚拟加工研究[J]. 系统仿真学报, 2008, 20(16): 4339-4343.PU Tai-ping, TANG Jin-yuan. Virtual machining process research of spur-gear based on CATIA V5[J]. Journal of System Simulation, 2008, 20(16): 4339-4343.

[13] Stadtfeld H. Advanced bevel gear technology[R]. New York: The Gleason Works, 2000: 20-30.

[14] 王军, 王小椿, 姜虹, 等. 螺旋锥齿轮齿面的三坐标测量[J].机械工程学报, 2003, 39(6): 151-154.WANG Jun, WANG Xiao-chun, JIANG Hong, et al. Coordinate measurement of tooth surface of spiral bevel gear[J]. Chinese Journal of Mechanical Engineering, 2003, 39(6): 151-154.