EMD的LabVIEW实现及其在滚动轴承故障信号分析中的应用
唐贵基,马万里,胡爱军
(华北电力大学 机械工程系,河北 保定 071003)
当滚动轴承发生故障时,其振动信号往往表现为非平稳的冲击特性。冲击性故障信号频带较宽,一般会激起零部件的高频固有振动。其振动信号特点为故障特征频率信号与各个高频固有振动信号发生幅值调制,因此对轴承故障信号分析的关键就是如何有效地提取高频调制故障信息。
Hibert-Huang变换(HHT)是由华裔科学家黄锷提出的处理非平稳信号的方法[1]。其中经验模态分解(EMD)是关键算法。EMD方法通过“筛”的方法将一个信号自适应地分解成若干个具有真实物理意义的本征模函数(IMF),IMF可以是调频或调幅信号,其频率大小依次从高到低排列,分解出的IMF更好地突出了信号的局部特征,因此可利用EMD方法将轴承故障信号自适应地分解成若干个窄带信号,从而提取故障信息。
EMD大多数是通过Matlab来实现,Matlab适合复杂的数值分析,但其用户界面效果较差,不适合用来开发测试系统。LabVIEW具有良好的用户界面,大大缩短了项目的开发周期,利用LabVIEW可快速地搭建虚拟测试系统[2]。但LabVIEW开发软件中不包含EMD算法,文献[3]通过mathscrip节点调用Matlab在LabVIEW中实现EMD算法,但是通过LabVIEW调用Matlab要进行大量的数据类型转换,当处理的数据较大时,其运行的速度将非常缓慢。因此根据EMD原理对LabVIEW软件进行二次开发,编写EMD程序,并通过包络解调的方法对EMD分解后的轴承故障信号进行分析。
1 EMD方法简介
EMD算法是将一个信号通过“筛”的方式分解为若干个IMF,对于信号x(t),EMD算法的流程如下[4]:
(1)确定信号x(t)所有极大值与极小值点;
(2)根据信号的极大值与极小值点,利用3次样条插值的方法分别构造x(t)的上、下包络线u(t)与v(t);
(3)求得信号的局部均值m(t)=[u(t)+v(t)]/2;
(4)用x(t)减去m(t)得到:h(t)=x(t)-m(t);
(5)判断h(t)是否满足IMF条件,如果满足则得到第1个IMF分量c1(t),否则重复以上步骤直到信号满足IMF条件为止;
(6)用x(t)减去c1(t)得到r(t),判断r(t)是否需要继续分解,如需要则用r(t)代替x(t)重复以上步骤,否则分解结束。
到此,信号EMD分解结束,信号x(t)分解为若干个IMF分量ci(t)与剩余分量r(t)之和。即
(1)
2 EMD的LabVIEW实现
2.1 编程实现
根据EMD算法的原理以及流程,由LabVIEW编写的主程序如图1所示。其中主程序中包含以下子VI:极值包络、局部均值、IMF判据、剩余量判断子VI。其功能分别为利用3次样条的方法计算信号上、下包络线;根据信号上、下包络线计算信号局部均值;判断当前信号是否为IMF;判断当前信号是否需要继续分解。其中最重要的为计算信号上、下包络线的极值包络子VI(程序如图2所示),极值包络子VI中还包含用于抑制端点效应的镜像极值延拓子VI。其中IMF判别准则利用文献[5]中所提出的方法,即通过3个参数的综合来判别IMF,由于篇幅的限制,IMF判据和端点效应抑制的具体理论可参见文献[1,5]。

图1 EMD主程序

图2 极值包络子VI程序
2.2 仿真信号分析
选用文献[5]中所用到的仿真信号,其信号为2个三角波与1个正弦波的叠加。对仿真信号应用LabVIEW所编写的EMD算法进行分解,原始信号以及分解结果如图3所示,分解结果与文献[5]中一致。由此可以说明利用LabVIEW编写的EMD算法能够正确地对信号进行分解。
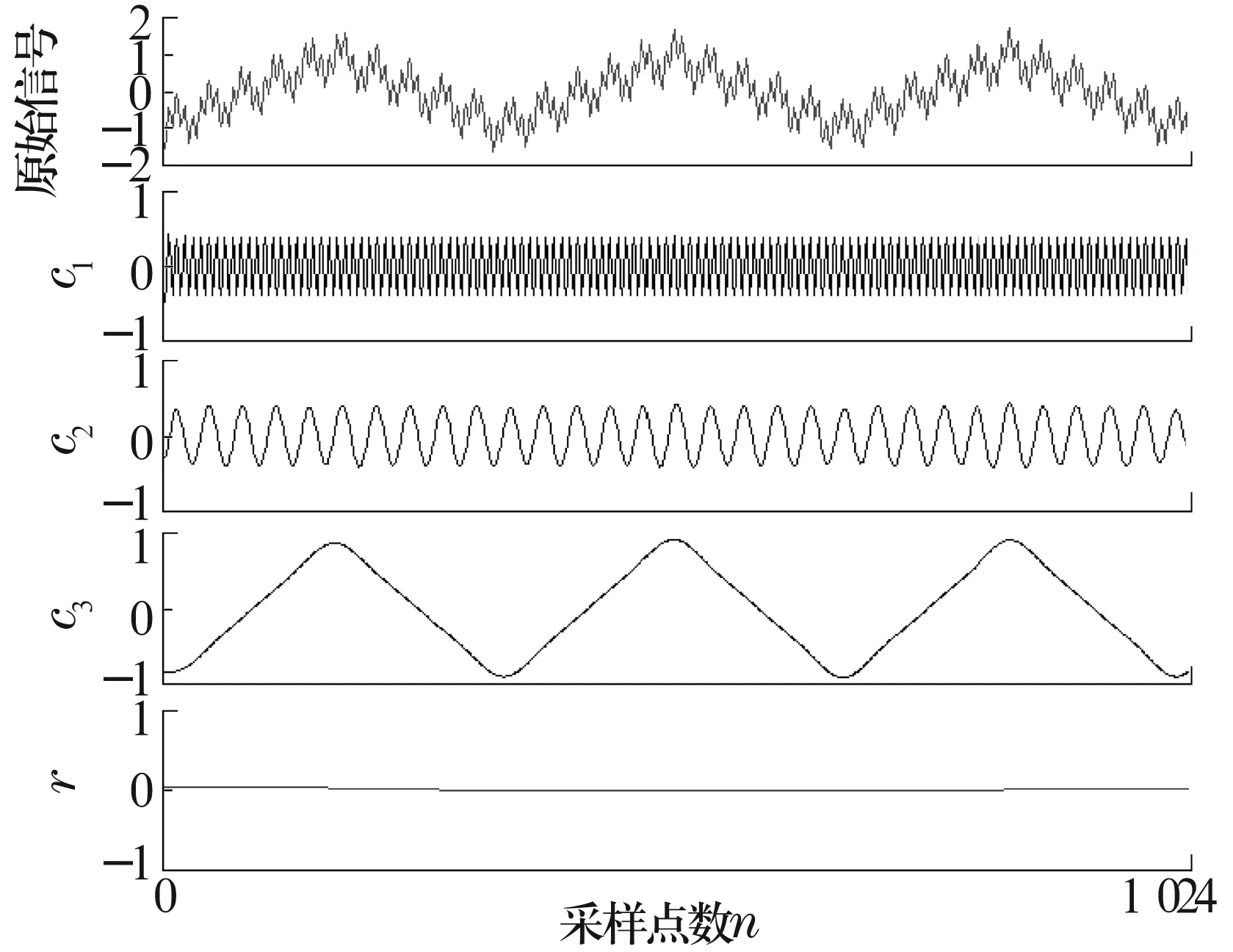
图3 仿真信号EMD分解结果
3 滚动轴承故障信号分析实例
3.1 基于EMD的包络解调方法
工程中应用的共振解调法的基本原理就是对加速度传感器拾取的轴承振动调制信号进行以共振频率为中心频率的窄带滤波,然后通过包络检波的方法提取出与冲击性故障信号频率一致的脉冲串[6]。但共振解调法需要根据经验预先设定带通滤波器的中心频率以及带宽,其选择的正确与否直接影响到诊断的准确度[7]。
基于上述分析,提出基于EMD的包络解调方法,其具体步骤为:
(1)对轴承振动信号进行EMD运算,得到若干IMF分量及剩余分量之和。IMF分量包含不同频率成分,其频率大小从高到低依次排列。
(2)对高频IMF进行包络解调,得到包络信号。信号的包络可以通过Hilbert变换[8]来实现。
(3)对得到的包络信号进行Fourier变换,从而获得信号的包络谱。
(4)对包络谱进行分析,根据谱上特征频率来诊断轴承故障类型。
由于EMD分解具有自适应性,从而避免了共振解调方法中中心频率以及带宽的选取。
3.2 实例分析
选取圆柱滚子轴承N205进行故障试验,轴承故障包括内圈、外圈和滚动体局部故障。信号选取轴承座垂直方向振动加速度信号,采样频率为12 800 Hz。试验台及测点位置如图4所示。当转轴转速为1 440 r/min时,其故障特征频率见表1。

图4 试验台及测点位置

表1 轴承各故障特征频率 Hz
3.2.1 内圈故障
轴承内圈故障信号的时域波形以及幅值谱如图5所示。从图5b中可以看到高频段频率信息比较丰富,基本上包含两个高频共振频带,直接从幅值谱上难以识别故障特征。利用LabVIEW编制的EMD算法对信号做分解,分解后的c1~c5如图6所示。c1~c5的幅值谱如图7所示。从图7中可以看到EMD算法自适应地将信号分解成若干不同频带的信号,频率从高到低依次排列。c1,c2分别对应两个明显的共振频带, 对c1做包络解调,其包络谱如图8所示。

图5 内圈故障信号及其幅值谱

图6 内圈故障信号EMD分解结果

图7 内圈故障信号c1~c5幅值谱

图8 内圈故障信号c1包络谱
当轴承内圈发生局部损伤时,根据损伤部分与滚动体发生冲击接触的位置不同,故障位置承载大小也不同。冲击振动的振幅大小不是均匀
的,而是周期性变化的,通常都以转轴的频率进行振幅调制,所以内圈故障信号应为零件高频固有振动信号、故障特征频率信号与转频信号调制而成。包络解调后的c1包络谱应存在转频及其倍频、故障特征频率及其倍频,并且在特征故障频率附近存在转频及其倍频的边带。从图8中可以看出在频率为24 Hz(转频)、172 Hz(轴承内圈故障特征频率)、148 Hz(转频边带)处存在明显的峰值。因此可以判断轴承发生了内圈局部故障。试验结果与理论分析一致。
3.2.2 外圈故障
外圈故障信号EMD分解后c1的包络谱如图9所示。与内圈故障信号不同,当外圈发生局部损伤时,故障位置和承载大小不发生变化,冲击振动的振幅大致相同,振动信号不以转频进行调制。包络解调后的c1包络谱中只包含故障特征频率及其倍频。从图9中可以看出在频率为116 Hz(外圈故障特征频率)及其倍频处存在明显峰值,基于上述分析可断定轴承发生了外圈局部故障,试验结果与理论分析一致。

图9 外圈故障信号c1包络谱
3.2.3 滚动体故障
滚动体故障信号EMD分解后c1的包络谱如图10所示。当滚动体发生局部损伤时,故障位置的承载大小随保持架的转动发生周期性的变化。因此故障信号为零件高频固有振动信号、故障特征频率信号与保持架转频信号调制而成。包络解调后的c1包络谱中应包含保持架转频及滚动体故障特征频率,在滚动体故障特征频率附近还应包含保持架转频的边带。从图10中可以看出在频率为10 Hz(保持架转频)、124 Hz(滚动体故障特征频率)和114 Hz(保持架转频边带)处存在明显的峰值。因此可以判断轴承发生了滚动体局部故障,试验结果与理论分析一致。
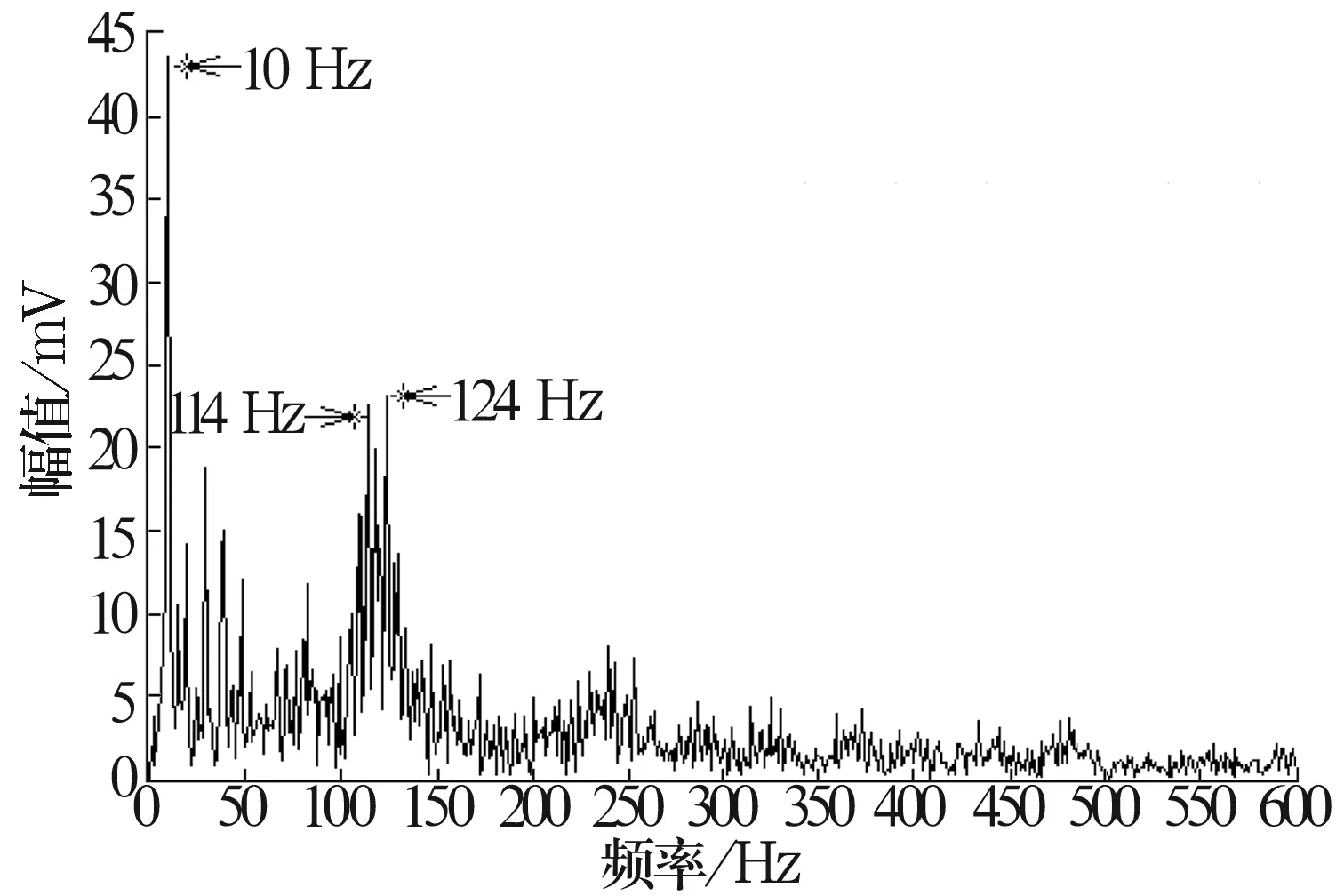
图10 滚动体故障信号c1包络谱
4 结束语
通过对轴承各种类型故障机理的详细分析并结合基于EMD的包络解调方法实现了轴承故障的精确诊断。同时基于LabVIEW的EMD算法的实现也为深入了解研究EMD提供了更为有利的环境。

